Here is the code from Lec_10_recognizer.hs . It is in Haskell

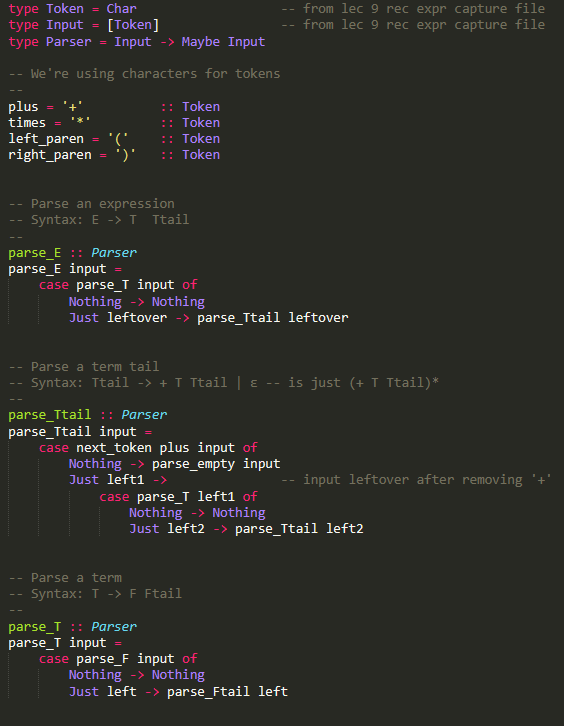
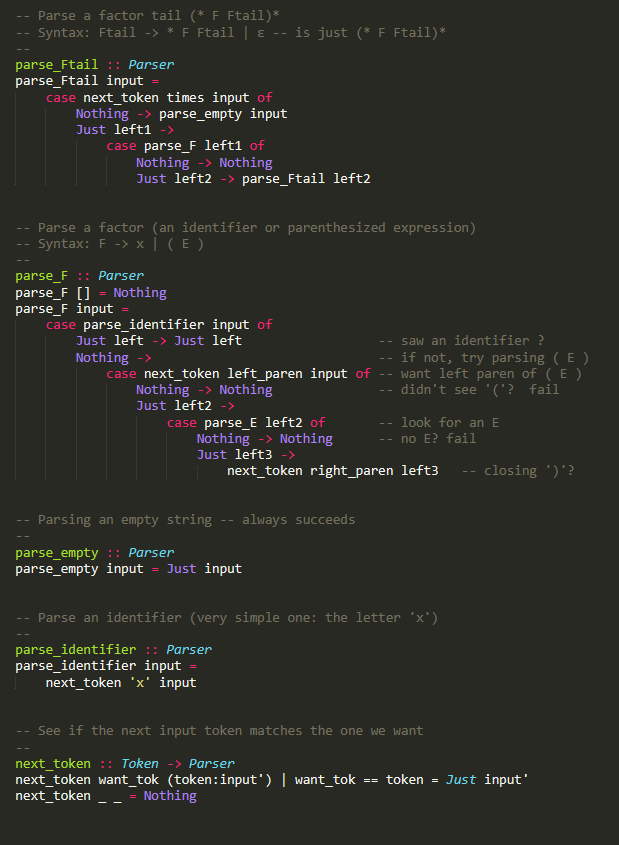
[6 pts) Take the Lec_10_recognizer.hs program and add a new rule for function calls, as factors. So we want calls like x(x,x), x(x* (x+x)), and so on. Include x( ) as a legal call. There is one detail: To keep the parser predictive, we can't have F x x other stuff because then an identifier x won't tell us which disjunct to use. A similar problem came up with E T T + E; you can solve it using the same idea (one clause with an option). You just have to write out the rule; you don't have to implement it in the Haskell program. Grading: 2 pts each: Handling x( ), x(one expression), x(many expressions separated by commas). Hint: Use a nonterminal for lists of expressions. type Token = Char type Input = [Token] type Parser = Input -> Maybe Input -- from lec 9 rec expr capture file -- from lec 9 rec expr capture file -- We're using characters for tokens plus = '+' times = '*' left_paren = 'c right_paren = ')' :: Token :: Token :: Token :: Token -- Parse an expression -- Syntax: E-> T Ttail parse_E :: Parser parse_E input = case parse_T input of Nothing -> Nothing Just leftover -> parse_Ttail leftover -- Parse a term tail -- Syntax: Ttail -> + T Ttail | -- is just (+ I Ttail)* parse_Ttail :: Parser parse_Ttail input = case next_token plus input of Nothing -> parse_empty input Just left1 -> -- input leftover after removing '+' case parse I lefti of Nothing -> Nothing Just left2 -> parse_Ttail left2 -- Parse a term -- Syntax: T -> F Ftail parse_1 :: Parser parse_T input = case parse_F input of Nothing -> Nothing Just left -> parse_Ftail left -- Parse a factor tail (* F Ftail)* -- Syntax: Ftail -> * F Ftail | E -- is just * F Ftail)* parse_Ftail :: Parser parse_Ftail input = case next_token times input of Nothing -> parse_empty input Just lefti -> case parse_F lefti of Nothing -> Nothing Just left2 -> parse_Ftail left2 -- Parse a factor (an identifier or parenthesized expression) -- Syntax: F-> XL (E) parse_F :: Parser parse_F [] = Nothing parse_F input = case parse_identifier input of Just left -> Just left -- saw an identifier ? Nothing -> -- if not, try parsing (E) case next token left paren input of -- want left paren of (E) Nothing -> Nothing -- didn't see '('? fail Just left2 -> case parse_E left2 of -- look for an E Nothing -> Nothing -- no E? fail Just left3 -> next_token right_paren left3 -- closing)?, -- Parsing an empty string -- always succeeds parse_empty :: Parser parse_empty input = Just input -- Parse an identifier (very simple one: the letter 'x') parse_identifier :: Parser parse_identifier input = next_token 'x' input -- See if the next input token matches the one we want next_token :: Token -> Parser next_token want_tok (token: input') next_token __ = Nothing want_tok == token = Just input [6 pts) Take the Lec_10_recognizer.hs program and add a new rule for function calls, as factors. So we want calls like x(x,x), x(x* (x+x)), and so on. Include x( ) as a legal call. There is one detail: To keep the parser predictive, we can't have F x x other stuff because then an identifier x won't tell us which disjunct to use. A similar problem came up with E T T + E; you can solve it using the same idea (one clause with an option). You just have to write out the rule; you don't have to implement it in the Haskell program. Grading: 2 pts each: Handling x( ), x(one expression), x(many expressions separated by commas). Hint: Use a nonterminal for lists of expressions. type Token = Char type Input = [Token] type Parser = Input -> Maybe Input -- from lec 9 rec expr capture file -- from lec 9 rec expr capture file -- We're using characters for tokens plus = '+' times = '*' left_paren = 'c right_paren = ')' :: Token :: Token :: Token :: Token -- Parse an expression -- Syntax: E-> T Ttail parse_E :: Parser parse_E input = case parse_T input of Nothing -> Nothing Just leftover -> parse_Ttail leftover -- Parse a term tail -- Syntax: Ttail -> + T Ttail | -- is just (+ I Ttail)* parse_Ttail :: Parser parse_Ttail input = case next_token plus input of Nothing -> parse_empty input Just left1 -> -- input leftover after removing '+' case parse I lefti of Nothing -> Nothing Just left2 -> parse_Ttail left2 -- Parse a term -- Syntax: T -> F Ftail parse_1 :: Parser parse_T input = case parse_F input of Nothing -> Nothing Just left -> parse_Ftail left -- Parse a factor tail (* F Ftail)* -- Syntax: Ftail -> * F Ftail | E -- is just * F Ftail)* parse_Ftail :: Parser parse_Ftail input = case next_token times input of Nothing -> parse_empty input Just lefti -> case parse_F lefti of Nothing -> Nothing Just left2 -> parse_Ftail left2 -- Parse a factor (an identifier or parenthesized expression) -- Syntax: F-> XL (E) parse_F :: Parser parse_F [] = Nothing parse_F input = case parse_identifier input of Just left -> Just left -- saw an identifier ? Nothing -> -- if not, try parsing (E) case next token left paren input of -- want left paren of (E) Nothing -> Nothing -- didn't see '('? fail Just left2 -> case parse_E left2 of -- look for an E Nothing -> Nothing -- no E? fail Just left3 -> next_token right_paren left3 -- closing)?, -- Parsing an empty string -- always succeeds parse_empty :: Parser parse_empty input = Just input -- Parse an identifier (very simple one: the letter 'x') parse_identifier :: Parser parse_identifier input = next_token 'x' input -- See if the next input token matches the one we want next_token :: Token -> Parser next_token want_tok (token: input') next_token __ = Nothing want_tok == token = Just input