Here is the data sheet

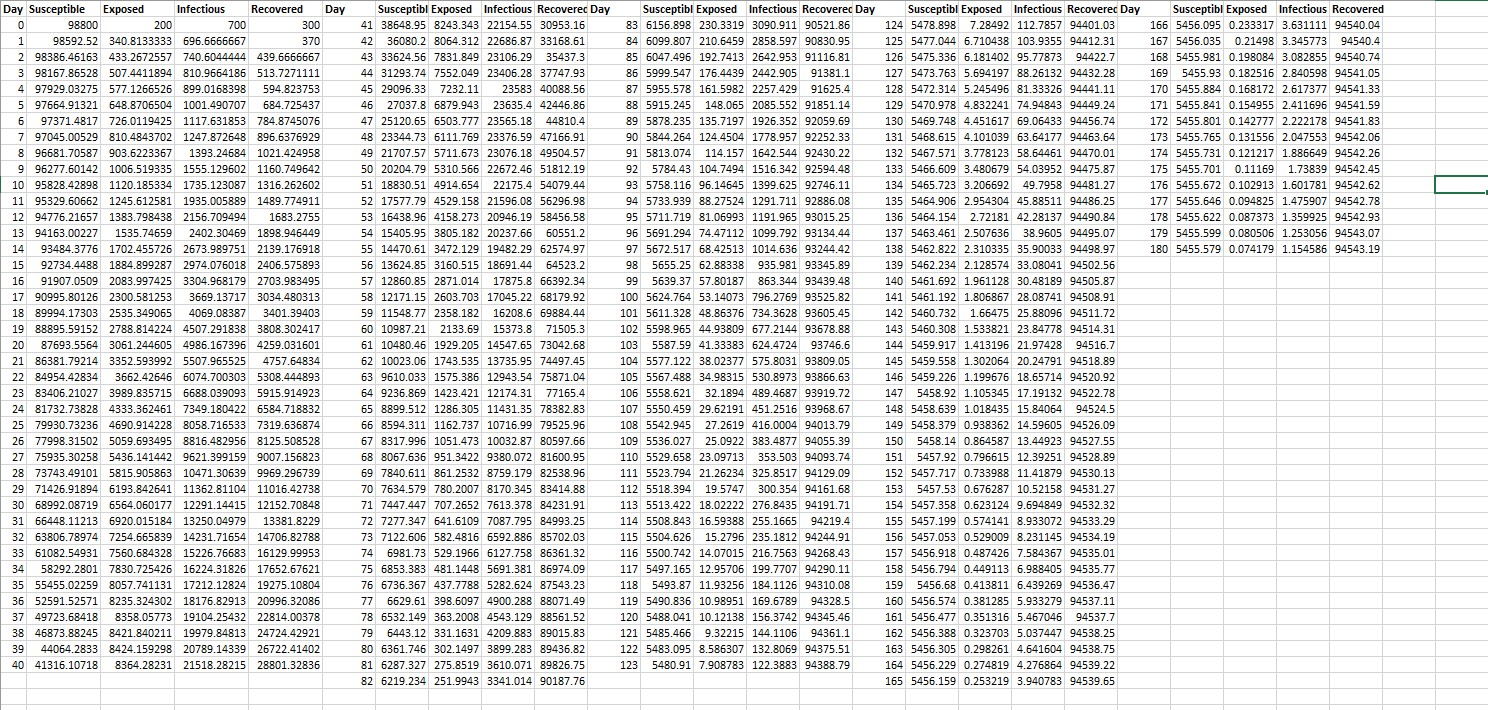
(2) In class, we used math to model how the number of people who are infected by an illness changes over time. As in class, we will assume that a certain illness is non-fatal and that everyone who catches it eventually recovers. The illness also confers immunity. Once a person recovers, they can never catch the illness again. In class, we used the SIR model to study an illness of this type. For this homework problem, we will improve the model to make its predictions a bit more accurate. For many illnesses, there is a period of time during which a person has contracted the illness but is not yet infectious. Such a person is called exposed. This is a poor term for it, but it's not my choice! By definition, an exposed person has definitely contracted the illness. They are just not able to spread it quite yet.) Our new SEIR model for illnesses has people moving from susceptible, to exposed, to infectious, and finally to recovered. Let's suppose that the illness is spreading through a fixed population consisting of 100,000 individuals. After a person is infected, there are three days during which the person cannot yet spread the illness to others (i.e., they are in the exposed group). The exposed person then becomes infectious for ten days. During any given day, every susceptible individual will come in contact with 0.01% of the total number of infectious individuals on that day. If a susceptible individual comes in contact with an infectious individual, then the susceptible individual has a 3% probability of catching the infection. On day t = 0, exactly 700 people are infectious, 200 are exposed (i.e., infected but not yet infectious), and 300 people have already recovered from the illness. Let S (t), E (t), 1 (t), and R (t) be the number of people on day t who are susceptible, exposed (i.e., infected but not infectious), infectious, and have recovered, respectively. Let S' (t), E' (t), I' (), and R' (t) be the change in the number of people on day t who are susceptible, exposed, infectious, and have recovered, respectively, (a) Find formulas for S' (t), E' (t), I' (t), and R' (t) based on the given assumptions and data. The example from class should be very helpful, so start with that example and adapt those answers to this situation, (b) The formulas from part (a) can be used with Excel to track the daily changes in the number of people in each category. The Excel file SEIR included in the homework link shows these results. Note. This is a great opportunity to check your answers from part (a). For example, you should be able to compute I (1) = 1 (0) + I'0). Do your equations produce the same numbers as the spreadsheet? Write a paragraph or two (with complete sentences) describing how this illness will pass through the population, according to our spreadsheet model. Also discuss the accuracy of these predictions. Be sure to include all of the following in your answer: When will the epidemic reach its peak? When will fewer than 1% of the population be infected? How many people will contract this illness at some time during the epidemic? How realistic are the assumptions of our model? What are the limitations of the model? How confident are you in the accuracy of your predictions? 44 31293.74 23583 40088 55 Susceptibl Exposed Infectious Recovered 166 5456.095 0.233317 3.631111 94540.04 167 5456.035 0.21498 3.345773 94540.4 168 5455.981 0.198084 3.082855 94540.74 169 5455.93 0.182516 2.840598 94541.05 170 5455.884 0.168172 2.617377 94541.33 171 5455.841 0.154955 2.411696 94541.59 172 5455 801 0 142777 2222178 94541 83 1/2 5455.801 0.142777 2.222178 94541.83 173 5455.765 0.131556 2.047553 94542.06 174 5455.731 0.121217 1.886649 94542.26 175 5455.701 0.11169 1.73839 94542.45 176 5455.672 0.102913 1.601781 94542.62 177 5455.646 0.094825 1.475907 94542.78 178 5455.622 0.087373 1.359925 94542.93 179 5455.599 0.080506 1.253056 94543.07 180 5455.579 0.074179 1.154586 94543.19 944227 A 97979 03220 17 00095 80126 2300.581253 105 3567.488 34.98315 530.8973 93866.63 Day Susceptible Exposed Infectious Recovered Day Susceptibl Exposed Infectious Recoverec Day Susceptibl Exposed Infectious Recoverec Day Susceptibl Exposed Infectious Recoverec Day 0 98800 200 700 300 41 38648.95 8243.343 22154.55 30953.16 83 6156.898 230.3319 3090.911 90521.86 124 5478.898 7.28492 112.7857 94401.03 1 98592.52 340.8133333 696.6666667 370 42 36080.2 8064.312 22686.87 33168.61 84 6099.807 210.6459 2858.597 90830.95 125 5477.044 6.710438 103.9355 94412.31 2 98386.46163 433.2672557 740.6044444 439.6666667 43 33624.56 7831.849 23106.29 35437.3 85 6047.496 192.7413 2642.953 91116.81 126 5475.336 6.181402 95.77873 3 98167.86528 507.4411894 810.9654186 513.7271111 7552.049 23406.28 37747.93 86 5090 547 176 1439 2442 905 013811 44 127 5473.763 5.694197 88.26132 94432.28 86 5999.547 176.4439 2442.905 91381.1 577.1266526 899.0168398 594.823753 45 29096 33 723211 87 5055 578 161 598) 2257 490 01695 45 29096.33 7232.11 87 5955.578 161.5982 2257.429 91625.4 128 5472.314 5.245496 81.33326 94441.11 5 97664.91321 648.8706504 1001.490707 684.725437 46 270378 6879 943 23635 4 47446 86 88 5915 245 148065 2085 552 01851 14 129 5470 978 4832241 74 94843 94449 24 46 27037.8 6879.943 23635.4 42446.86 88 5915.245 148.065 2085.552 91851.14 129 5470.978 4.832241 74.94843 94449.24 6 97371.4817 726.0119425 1117,631853 784.8745076 89 5878 235 135 7197 1926 357 92059 69 697371.4817 726.0119425 1117.631853 784.8745076 47 25120.65 6503.777 23565.18 44810.4 89 5878.235 135.7197 1926.352 92059.69 130 5469.748 4.451617 69.06433 94456.74 797045.00529 810.4843702 1247.872648 896.6376929 48 23344.73 6111.769 23376.59 47166.91 90 5844.264 124.4504 1778.957 92252.33 131 5468.615 4.101039 63.64177 94463.64 8 96681.70587 903.6223367 1393.24684 1021.424958 49 21707.57 5711.673 23076.18 49504.57 91 5813.074 114.157 1642.544 92430.22 132 5457.571 3.778123 58.64461 94470.01 06277 60142 1006 519335 1555 120602 1160 740642 996277.601421006.519335 1555.129602 1160.749642 50 20204.79 5310.566 22672.46 51812.19 925784.43 104.7494 1516.342 92594.48 133 5466.609 3.480679 54.03952 94475.87 10 95828.42898 1120.185334 1735.123087 1316.262602 51 18830.51 4914.654 22175.4 54079.44 93 5758.116 96.14645 1399.625 92746.11 134 5465./23 3.206b9249.7958 94481.27 94 5733.939 88.27524 1291.711 92886.08 11 95329.60662 1245.612581 1935.005889 1489.774911 52 17577.79 4529.158 21596.08 56296.98 135 5464.906 2.954304 45.88511 94486.25 12 94776.21657 1383.798438 2156.709494 1683.2755 53 16438.96 4158.273 20946.19 58456.58 95 5711.719 81.06993 1191.965 93015.25 136 5464.154 2.72181 42.28137 94490.84 2402 27459 1898 046240 06 5401 204 74 47112 1090 707 031344 137 5463.461 2507636 38 9505 0410507 15 94163.00227 1535.74659 2402.30469 1898.946449 54 15405.95 3805.182 20237.66 60551.2 137 5463.461 2.507636 38.9605 94495.07 93484 3776 1702.455726 2673.989751 2139.176918 96 5691.294 74.47112 1099.792 93134.44 12 138 5462 822 2310335 35 90033 99498 97 14 55 14470.61 3472.129 19482.29 62574.97 97 5672.517 68.42513 1014.636 93244.42 09731 MARS 188A 800287 0974 076018 2406 575893 138 5462.822 2.310335 35.90033 94498.97 15 15 92734.4488 1884.899287 2974.076018 2406.575893 56 13624.85 3160.515 18691.44 64523.2 98 5655.25 62.88338 935.981 93345.89 139 5462.234 2.128574 33.08041 94502.56 16 91907.0509 2083.997425 3304.968179 2703.983495 57 12860.85 2871.014 17875.8 66392.34 995639.37 57.80187 863.344 93439.48 140 5461.692 1.961128 30.48189 94505.87 3669.13717 3034.480313 58 12171.15 2603.703 17045.22 68179.92 100 5624.764 53.14073 796.2769 93525.82 141 5461.192 1.806867 28.08741 94508.91 19 BORA 17802 2520 240CE 18 89994.17303 2535.349065 4069.08387 3401.39403 101 5611.328 48.86376 734.3628 93605.45 59 11548.77 2358.182 16208.6 69884.44 19 38895 59152 2788 814724 4507 291838 3808 302417 142 5460.732 1.66475 25.88096 94511.72 19 88895.59152 2788.814224 4507.291838 3808.302417 60 10987.21 2133.69 15373.8 71505.3 102 5598.965 44.93809 677.2144 93678.88 143 5460.308 1.533821 23.84778 94514.31 103 5597 50 44 22202 C 270 274CC 20 87693.5564 3061.244605 4986.167396 4259.031601 61 10480.46 1929.205 14547.65 73042.68 103 5587.59 41.33383 624.4724 93746.6 144 5459.917 1.413196 21.97428 94516.7 21 86381.79214 3352.593992 5507.965525 4757.64834 62 10023.06 1743.535 13735.95 74497.45 104 5577.122 38.02377 575.8031 93809.05 145 5459.558 1.302064 20.24791 94518.89 3662 42645 6074 700303 5308444823 22 84954.42834 3662.42646 6074.700303 5308.444893 63 9610.033 1575.386 12943.54 75871.04 23 83406.21027 3989.835715 6688.039093 5915.914923 146 5459.226 1.199676 18.65714 94520.92 106 5558 621 32.1804 1804687 030107 64 9236.869 1423.421 12174.31 77165.4 106 5558.621 32.1894 489.4687 93919.72 5458.92 1.105345 17.19132 94522.78 24 81732 73828 2333 362461 7340 181422 5584 718832 24 81732.73828 4333.362461 7349.180422 6584.718832 107 5550.459 29.62191 451.2516 93968.67 65 8899.512 1286.305 11431.35 78382.83 148 5458.639 1.018435 15.84064 945245 2579930.73236 4690.914228 8058.716533 7319.636874 66 8594.311 1162.737 10716.99 79525.96 108 5542.945 27.2619 416.0004 149 5458.379 0.938362 14.59605 94526.09 2677998.31502 5059.693495 8816.482956 8125.508528 67 8317.996 1051.473 10032.87 80597.66 109 5536.027 25.0922 383.4877 94055.39 150 5458.14 0.864587 13.44923 94527.55 27 75935.30258 5436.141442 9621.399159 9007.156823 68 8067.636 951.3422 9380.072 81600.95 110 5529.658 23.09713 353.503 94093.74 151 5457.92 0.796615 12.39251 94528.89 28 73743.49101 5815.905863 10471.30639 9969.296739 69 7840.611 861.2532 8759.179 82538.96 111 5523.794 21.26234 325.8517 94129.09 152 5457.717 0.733988 11.41879 94530.13 29 71426.91894 6193.842641 11362.81104 11016.42738 70 7634.579 780.2007 8170.345 83414.88 112 5518.394 19.5747 300.354 94161.68 153 5457.53 0.676287 10.52158 94531.27 30 68992.08719 6564.060177 12291.14415 12152.70848 71 7447.447 707.2652 7613.378 84231.91 113 5513.422 18.02222 276.8435 94191.71 154 5457.358 0.623124 9.694849 94532.32 31 66448.11213 6920.015184 13250.04979 on 10 er - 2 m 2 13381.8229 72 7277.347 641.6109 7087.795 84993.25 114 5508.843 16.59388 255.1665 94219.4 155 5457.199 0.574141 8.933072 94533.29 *** 1.200 2100 212 32 63806.78974 7254.665839 14231.71654 14706.82788 73 7122.606 582.4816 6592.886 85702.03 www.ro 115 5504.626 15.2796 235.1812 94244.91 156 5457.053 0.529009 8.231145 94534.19 1 102 103 33 61082.54931 7560.684328 15226.76683 16129.99953 74 6981.73 529.1966 6127.758 86361.32 116 5500.742 14.07015 216.7563 94268.43 157 5456.918 0.487426 7.584367 94535.01 10 a 141 14 14 100 470 47 34 58292.2801 7830.725426 16224.31826 17652.67621 117 5497.165 12.95706 199.7707 94290.11 75 6853.383 481.1448 5691.381 86974.09 158 5456.794 0.449113 6.988405 94535.77 14. no.. 1 212 1 1 1040 are acco3944 35 55455.02259 8057.741131 17212.12824 19275.10804 118 5493.87 11.93256 184.1126 94310.08 76 6736.367 437.7788 5282.624 87543.23 159 5456.68 0.413811 6.439269 94536.47 ---- 30.01 102 10.12. 1 or 0740 44 36 52591.52571 8235.324302 18176.82913 20996.32086 77 6629.61 398.6097 4900.288 88071.49 119 5490.836 10.98951 169.6789 94328.5 160 5456.574 0.381285 5.933279 94537.11 2022 10. 2020 37 49723.68418 8358.05773 19104.25432 22814.00378 78 6532.149 363.2008 4543.129 88561.52 120 5488.041 10.12138 156.3742 94345.46 161 5456.477 0.351316 5.467046 94537.7 38 46873.88245 8421.840211 19979.84813 24724.42921 79 6443.12 331.1631 4209.883 89015.83 121 5485.466 9.32215 144. 1106 94361.1 162 5456.388 0.323703 5.037447 94538.25 39 44064.2833 8424.159298 20789.14339 26722.41402 80 6361.746 302.1497 3899.283 89436.82 122 5483.095 8.586307 132.8069 94375.51 163 5456.305 0.298261 4.641604 94538.75 40 41316.10718 8364.28231 21518.28215 28801.32836 81 6287.327 275.8519 3610.071 89826.75 123 5480.91 7.908783 122.3883 94388.79 164 5456.229 0.274819 4.276864 94539.22 82 6219.234 251.9943 3341.014 90187.76 165 5456.159 0.253219 3.940783 94539.65 94013.79 (2) In class, we used math to model how the number of people who are infected by an illness changes over time. As in class, we will assume that a certain illness is non-fatal and that everyone who catches it eventually recovers. The illness also confers immunity. Once a person recovers, they can never catch the illness again. In class, we used the SIR model to study an illness of this type. For this homework problem, we will improve the model to make its predictions a bit more accurate. For many illnesses, there is a period of time during which a person has contracted the illness but is not yet infectious. Such a person is called exposed. This is a poor term for it, but it's not my choice! By definition, an exposed person has definitely contracted the illness. They are just not able to spread it quite yet.) Our new SEIR model for illnesses has people moving from susceptible, to exposed, to infectious, and finally to recovered. Let's suppose that the illness is spreading through a fixed population consisting of 100,000 individuals. After a person is infected, there are three days during which the person cannot yet spread the illness to others (i.e., they are in the exposed group). The exposed person then becomes infectious for ten days. During any given day, every susceptible individual will come in contact with 0.01% of the total number of infectious individuals on that day. If a susceptible individual comes in contact with an infectious individual, then the susceptible individual has a 3% probability of catching the infection. On day t = 0, exactly 700 people are infectious, 200 are exposed (i.e., infected but not yet infectious), and 300 people have already recovered from the illness. Let S (t), E (t), 1 (t), and R (t) be the number of people on day t who are susceptible, exposed (i.e., infected but not infectious), infectious, and have recovered, respectively. Let S' (t), E' (t), I' (), and R' (t) be the change in the number of people on day t who are susceptible, exposed, infectious, and have recovered, respectively, (a) Find formulas for S' (t), E' (t), I' (t), and R' (t) based on the given assumptions and data. The example from class should be very helpful, so start with that example and adapt those answers to this situation, (b) The formulas from part (a) can be used with Excel to track the daily changes in the number of people in each category. The Excel file SEIR included in the homework link shows these results. Note. This is a great opportunity to check your answers from part (a). For example, you should be able to compute I (1) = 1 (0) + I'0). Do your equations produce the same numbers as the spreadsheet? Write a paragraph or two (with complete sentences) describing how this illness will pass through the population, according to our spreadsheet model. Also discuss the accuracy of these predictions. Be sure to include all of the following in your answer: When will the epidemic reach its peak? When will fewer than 1% of the population be infected? How many people will contract this illness at some time during the epidemic? How realistic are the assumptions of our model? What are the limitations of the model? How confident are you in the accuracy of your predictions? 44 31293.74 23583 40088 55 Susceptibl Exposed Infectious Recovered 166 5456.095 0.233317 3.631111 94540.04 167 5456.035 0.21498 3.345773 94540.4 168 5455.981 0.198084 3.082855 94540.74 169 5455.93 0.182516 2.840598 94541.05 170 5455.884 0.168172 2.617377 94541.33 171 5455.841 0.154955 2.411696 94541.59 172 5455 801 0 142777 2222178 94541 83 1/2 5455.801 0.142777 2.222178 94541.83 173 5455.765 0.131556 2.047553 94542.06 174 5455.731 0.121217 1.886649 94542.26 175 5455.701 0.11169 1.73839 94542.45 176 5455.672 0.102913 1.601781 94542.62 177 5455.646 0.094825 1.475907 94542.78 178 5455.622 0.087373 1.359925 94542.93 179 5455.599 0.080506 1.253056 94543.07 180 5455.579 0.074179 1.154586 94543.19 944227 A 97979 03220 17 00095 80126 2300.581253 105 3567.488 34.98315 530.8973 93866.63 Day Susceptible Exposed Infectious Recovered Day Susceptibl Exposed Infectious Recoverec Day Susceptibl Exposed Infectious Recoverec Day Susceptibl Exposed Infectious Recoverec Day 0 98800 200 700 300 41 38648.95 8243.343 22154.55 30953.16 83 6156.898 230.3319 3090.911 90521.86 124 5478.898 7.28492 112.7857 94401.03 1 98592.52 340.8133333 696.6666667 370 42 36080.2 8064.312 22686.87 33168.61 84 6099.807 210.6459 2858.597 90830.95 125 5477.044 6.710438 103.9355 94412.31 2 98386.46163 433.2672557 740.6044444 439.6666667 43 33624.56 7831.849 23106.29 35437.3 85 6047.496 192.7413 2642.953 91116.81 126 5475.336 6.181402 95.77873 3 98167.86528 507.4411894 810.9654186 513.7271111 7552.049 23406.28 37747.93 86 5090 547 176 1439 2442 905 013811 44 127 5473.763 5.694197 88.26132 94432.28 86 5999.547 176.4439 2442.905 91381.1 577.1266526 899.0168398 594.823753 45 29096 33 723211 87 5055 578 161 598) 2257 490 01695 45 29096.33 7232.11 87 5955.578 161.5982 2257.429 91625.4 128 5472.314 5.245496 81.33326 94441.11 5 97664.91321 648.8706504 1001.490707 684.725437 46 270378 6879 943 23635 4 47446 86 88 5915 245 148065 2085 552 01851 14 129 5470 978 4832241 74 94843 94449 24 46 27037.8 6879.943 23635.4 42446.86 88 5915.245 148.065 2085.552 91851.14 129 5470.978 4.832241 74.94843 94449.24 6 97371.4817 726.0119425 1117,631853 784.8745076 89 5878 235 135 7197 1926 357 92059 69 697371.4817 726.0119425 1117.631853 784.8745076 47 25120.65 6503.777 23565.18 44810.4 89 5878.235 135.7197 1926.352 92059.69 130 5469.748 4.451617 69.06433 94456.74 797045.00529 810.4843702 1247.872648 896.6376929 48 23344.73 6111.769 23376.59 47166.91 90 5844.264 124.4504 1778.957 92252.33 131 5468.615 4.101039 63.64177 94463.64 8 96681.70587 903.6223367 1393.24684 1021.424958 49 21707.57 5711.673 23076.18 49504.57 91 5813.074 114.157 1642.544 92430.22 132 5457.571 3.778123 58.64461 94470.01 06277 60142 1006 519335 1555 120602 1160 740642 996277.601421006.519335 1555.129602 1160.749642 50 20204.79 5310.566 22672.46 51812.19 925784.43 104.7494 1516.342 92594.48 133 5466.609 3.480679 54.03952 94475.87 10 95828.42898 1120.185334 1735.123087 1316.262602 51 18830.51 4914.654 22175.4 54079.44 93 5758.116 96.14645 1399.625 92746.11 134 5465./23 3.206b9249.7958 94481.27 94 5733.939 88.27524 1291.711 92886.08 11 95329.60662 1245.612581 1935.005889 1489.774911 52 17577.79 4529.158 21596.08 56296.98 135 5464.906 2.954304 45.88511 94486.25 12 94776.21657 1383.798438 2156.709494 1683.2755 53 16438.96 4158.273 20946.19 58456.58 95 5711.719 81.06993 1191.965 93015.25 136 5464.154 2.72181 42.28137 94490.84 2402 27459 1898 046240 06 5401 204 74 47112 1090 707 031344 137 5463.461 2507636 38 9505 0410507 15 94163.00227 1535.74659 2402.30469 1898.946449 54 15405.95 3805.182 20237.66 60551.2 137 5463.461 2.507636 38.9605 94495.07 93484 3776 1702.455726 2673.989751 2139.176918 96 5691.294 74.47112 1099.792 93134.44 12 138 5462 822 2310335 35 90033 99498 97 14 55 14470.61 3472.129 19482.29 62574.97 97 5672.517 68.42513 1014.636 93244.42 09731 MARS 188A 800287 0974 076018 2406 575893 138 5462.822 2.310335 35.90033 94498.97 15 15 92734.4488 1884.899287 2974.076018 2406.575893 56 13624.85 3160.515 18691.44 64523.2 98 5655.25 62.88338 935.981 93345.89 139 5462.234 2.128574 33.08041 94502.56 16 91907.0509 2083.997425 3304.968179 2703.983495 57 12860.85 2871.014 17875.8 66392.34 995639.37 57.80187 863.344 93439.48 140 5461.692 1.961128 30.48189 94505.87 3669.13717 3034.480313 58 12171.15 2603.703 17045.22 68179.92 100 5624.764 53.14073 796.2769 93525.82 141 5461.192 1.806867 28.08741 94508.91 19 BORA 17802 2520 240CE 18 89994.17303 2535.349065 4069.08387 3401.39403 101 5611.328 48.86376 734.3628 93605.45 59 11548.77 2358.182 16208.6 69884.44 19 38895 59152 2788 814724 4507 291838 3808 302417 142 5460.732 1.66475 25.88096 94511.72 19 88895.59152 2788.814224 4507.291838 3808.302417 60 10987.21 2133.69 15373.8 71505.3 102 5598.965 44.93809 677.2144 93678.88 143 5460.308 1.533821 23.84778 94514.31 103 5597 50 44 22202 C 270 274CC 20 87693.5564 3061.244605 4986.167396 4259.031601 61 10480.46 1929.205 14547.65 73042.68 103 5587.59 41.33383 624.4724 93746.6 144 5459.917 1.413196 21.97428 94516.7 21 86381.79214 3352.593992 5507.965525 4757.64834 62 10023.06 1743.535 13735.95 74497.45 104 5577.122 38.02377 575.8031 93809.05 145 5459.558 1.302064 20.24791 94518.89 3662 42645 6074 700303 5308444823 22 84954.42834 3662.42646 6074.700303 5308.444893 63 9610.033 1575.386 12943.54 75871.04 23 83406.21027 3989.835715 6688.039093 5915.914923 146 5459.226 1.199676 18.65714 94520.92 106 5558 621 32.1804 1804687 030107 64 9236.869 1423.421 12174.31 77165.4 106 5558.621 32.1894 489.4687 93919.72 5458.92 1.105345 17.19132 94522.78 24 81732 73828 2333 362461 7340 181422 5584 718832 24 81732.73828 4333.362461 7349.180422 6584.718832 107 5550.459 29.62191 451.2516 93968.67 65 8899.512 1286.305 11431.35 78382.83 148 5458.639 1.018435 15.84064 945245 2579930.73236 4690.914228 8058.716533 7319.636874 66 8594.311 1162.737 10716.99 79525.96 108 5542.945 27.2619 416.0004 149 5458.379 0.938362 14.59605 94526.09 2677998.31502 5059.693495 8816.482956 8125.508528 67 8317.996 1051.473 10032.87 80597.66 109 5536.027 25.0922 383.4877 94055.39 150 5458.14 0.864587 13.44923 94527.55 27 75935.30258 5436.141442 9621.399159 9007.156823 68 8067.636 951.3422 9380.072 81600.95 110 5529.658 23.09713 353.503 94093.74 151 5457.92 0.796615 12.39251 94528.89 28 73743.49101 5815.905863 10471.30639 9969.296739 69 7840.611 861.2532 8759.179 82538.96 111 5523.794 21.26234 325.8517 94129.09 152 5457.717 0.733988 11.41879 94530.13 29 71426.91894 6193.842641 11362.81104 11016.42738 70 7634.579 780.2007 8170.345 83414.88 112 5518.394 19.5747 300.354 94161.68 153 5457.53 0.676287 10.52158 94531.27 30 68992.08719 6564.060177 12291.14415 12152.70848 71 7447.447 707.2652 7613.378 84231.91 113 5513.422 18.02222 276.8435 94191.71 154 5457.358 0.623124 9.694849 94532.32 31 66448.11213 6920.015184 13250.04979 on 10 er - 2 m 2 13381.8229 72 7277.347 641.6109 7087.795 84993.25 114 5508.843 16.59388 255.1665 94219.4 155 5457.199 0.574141 8.933072 94533.29 *** 1.200 2100 212 32 63806.78974 7254.665839 14231.71654 14706.82788 73 7122.606 582.4816 6592.886 85702.03 www.ro 115 5504.626 15.2796 235.1812 94244.91 156 5457.053 0.529009 8.231145 94534.19 1 102 103 33 61082.54931 7560.684328 15226.76683 16129.99953 74 6981.73 529.1966 6127.758 86361.32 116 5500.742 14.07015 216.7563 94268.43 157 5456.918 0.487426 7.584367 94535.01 10 a 141 14 14 100 470 47 34 58292.2801 7830.725426 16224.31826 17652.67621 117 5497.165 12.95706 199.7707 94290.11 75 6853.383 481.1448 5691.381 86974.09 158 5456.794 0.449113 6.988405 94535.77 14. no.. 1 212 1 1 1040 are acco3944 35 55455.02259 8057.741131 17212.12824 19275.10804 118 5493.87 11.93256 184.1126 94310.08 76 6736.367 437.7788 5282.624 87543.23 159 5456.68 0.413811 6.439269 94536.47 ---- 30.01 102 10.12. 1 or 0740 44 36 52591.52571 8235.324302 18176.82913 20996.32086 77 6629.61 398.6097 4900.288 88071.49 119 5490.836 10.98951 169.6789 94328.5 160 5456.574 0.381285 5.933279 94537.11 2022 10. 2020 37 49723.68418 8358.05773 19104.25432 22814.00378 78 6532.149 363.2008 4543.129 88561.52 120 5488.041 10.12138 156.3742 94345.46 161 5456.477 0.351316 5.467046 94537.7 38 46873.88245 8421.840211 19979.84813 24724.42921 79 6443.12 331.1631 4209.883 89015.83 121 5485.466 9.32215 144. 1106 94361.1 162 5456.388 0.323703 5.037447 94538.25 39 44064.2833 8424.159298 20789.14339 26722.41402 80 6361.746 302.1497 3899.283 89436.82 122 5483.095 8.586307 132.8069 94375.51 163 5456.305 0.298261 4.641604 94538.75 40 41316.10718 8364.28231 21518.28215 28801.32836 81 6287.327 275.8519 3610.071 89826.75 123 5480.91 7.908783 122.3883 94388.79 164 5456.229 0.274819 4.276864 94539.22 82 6219.234 251.9943 3341.014 90187.76 165 5456.159 0.253219 3.940783 94539.65 94013.79