Hi course hero! May you please break down so I may understand the material. In clear text please and thank you!

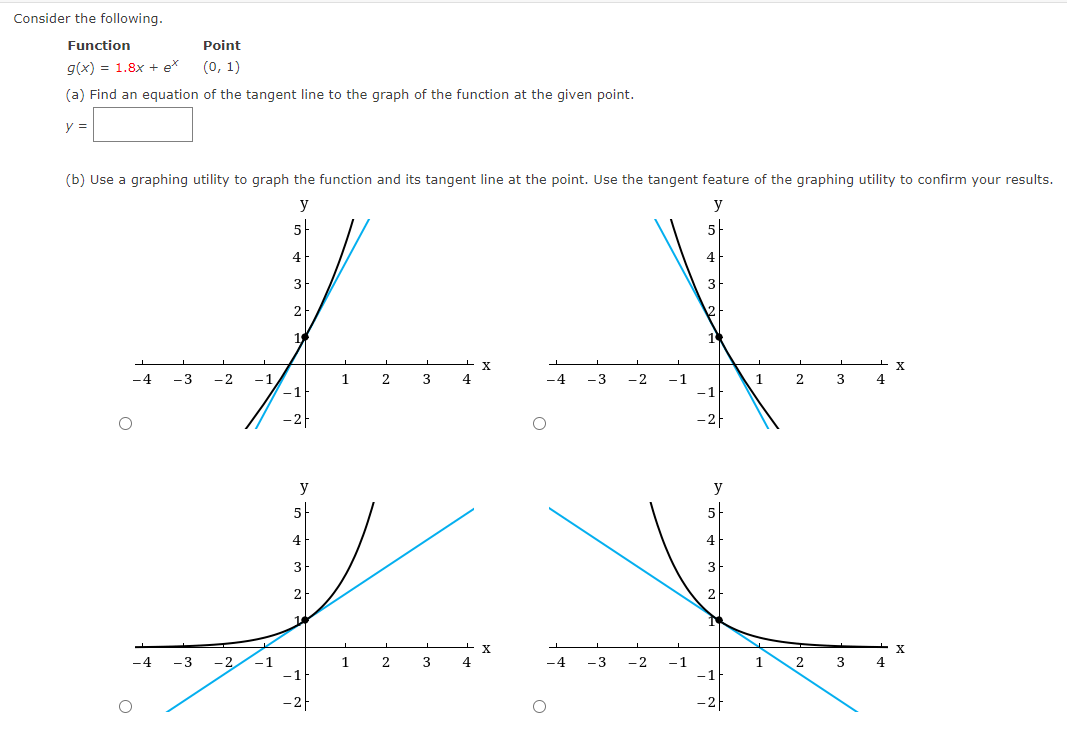
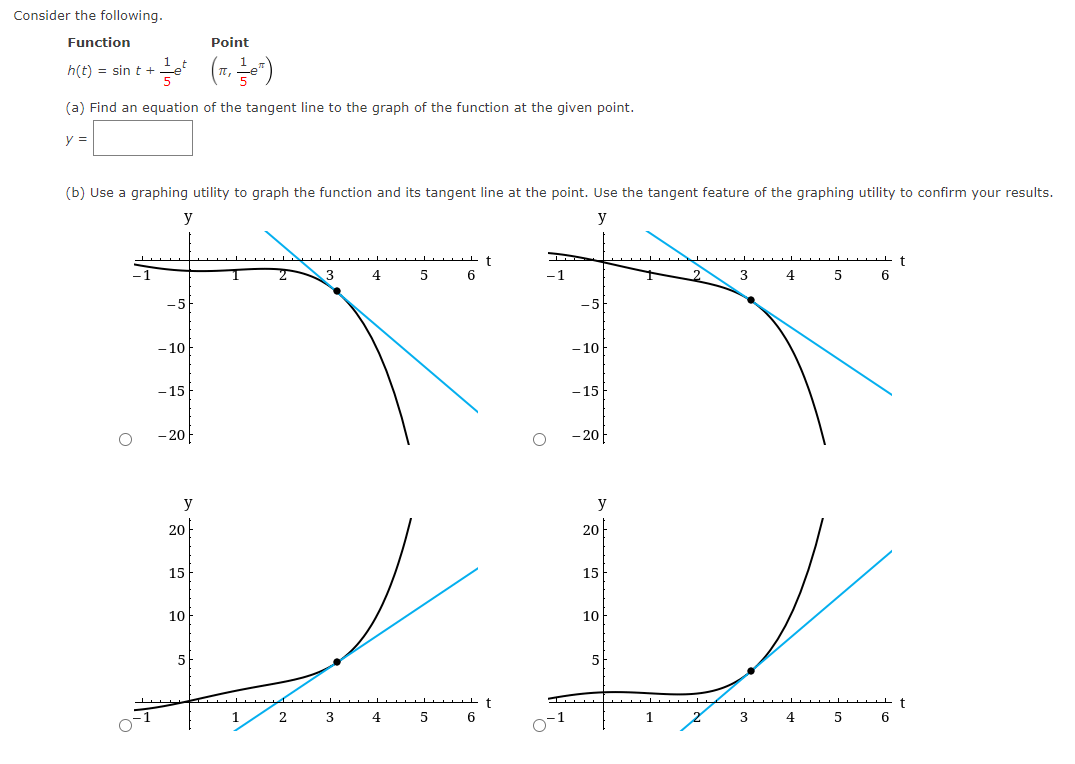
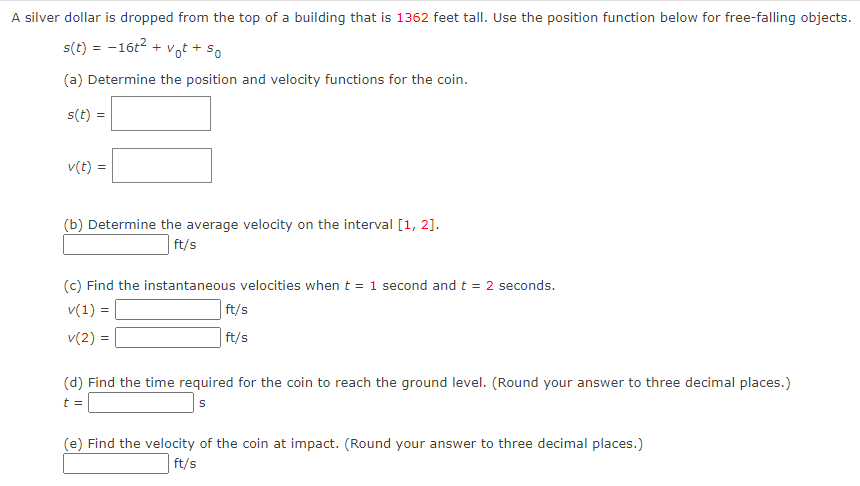
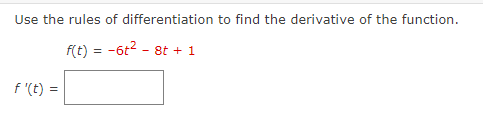
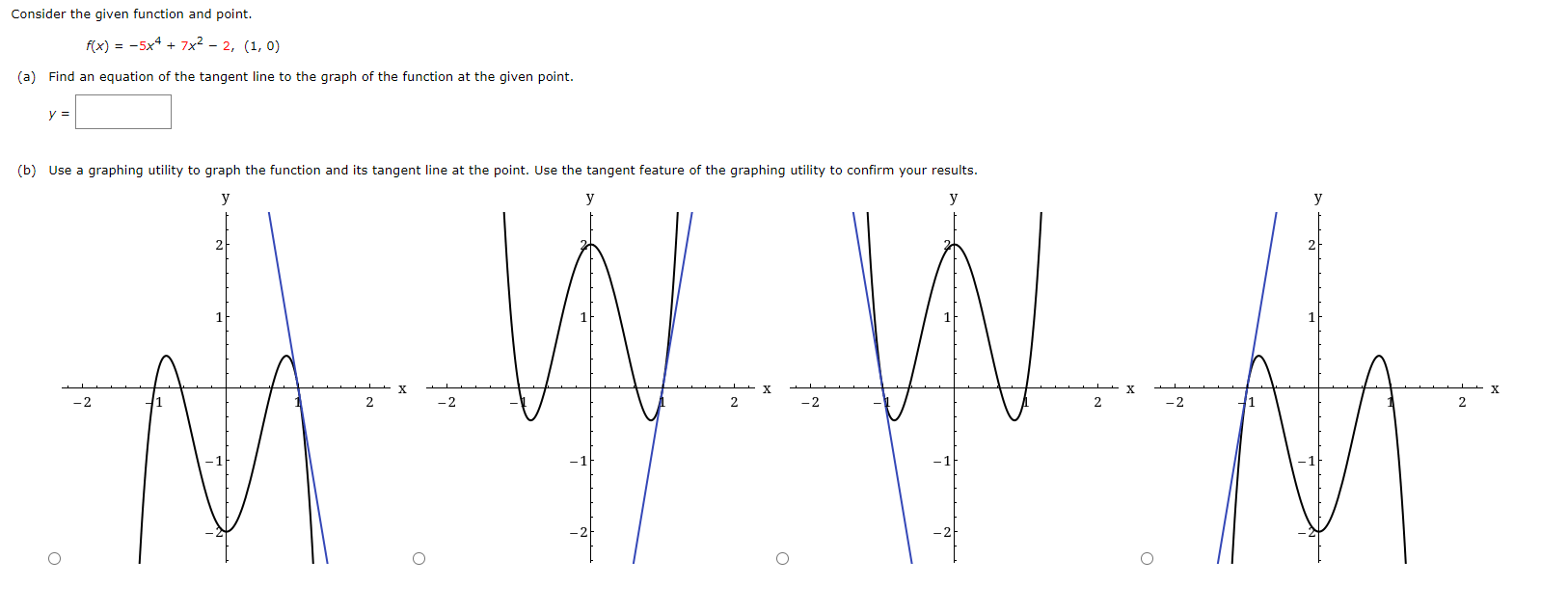
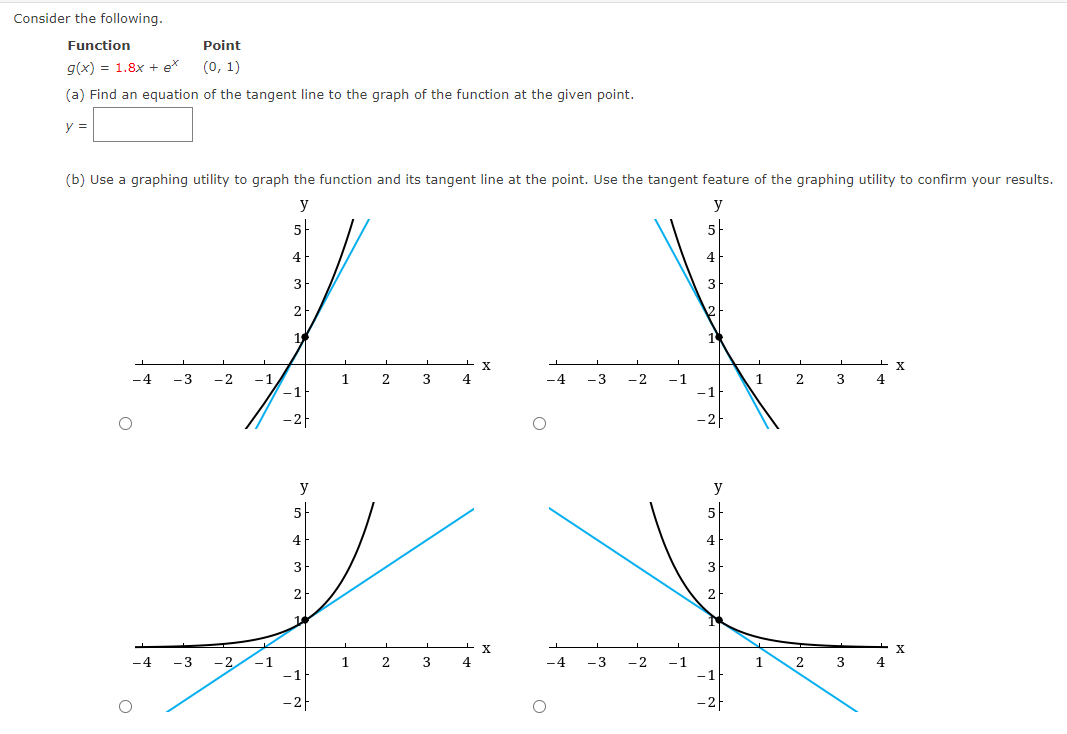
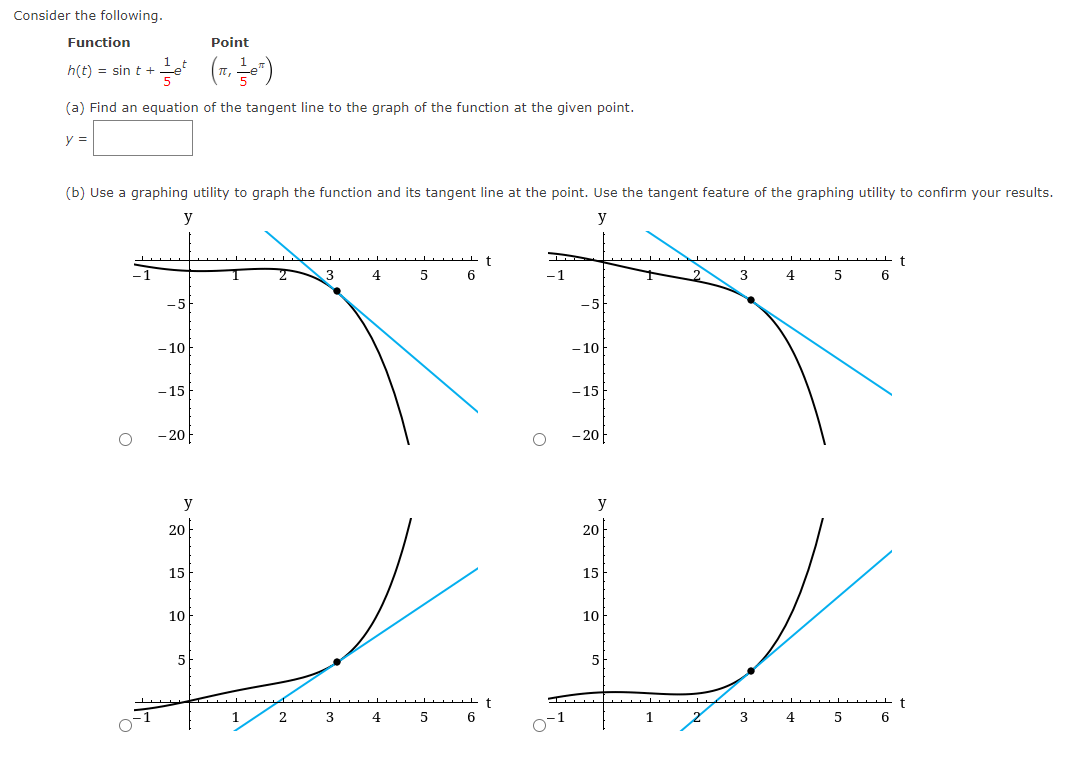
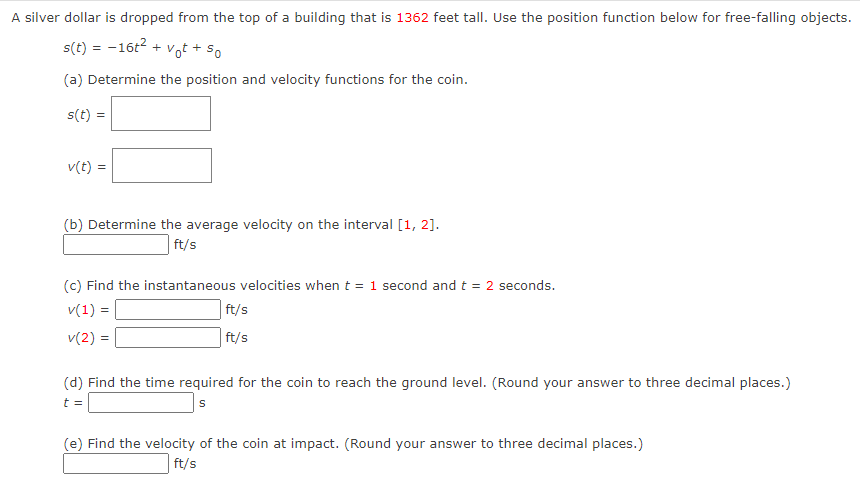
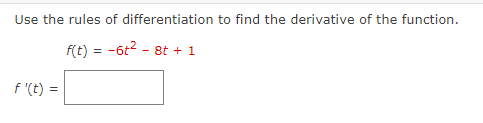
Use the rules of differentiation to find the derivative of the function. 4 5Find the derivative of the function 4x- + 3 A( x ) F '( x) Find the derivative of the function. 3 F(x ) x 4 X F(X) = Consider the following. Function Point 90:} = 1.8x + e" {0, 1) (a) Find an equation of the tangent line to the graph of the function at the given point. y: (b) Use a graphing utility to graph the function and its tangent line at the point. Use the tangent feature of the graphing utility to confirm your results. Y Y Co n5ider the following. Function Point Mt] = sin t + ie'L (:7, ie") 5 5 {a} Find an equation of the tangent line to the graph of the function at the given point. J' (b) Use a graphing utilitg.r to graph the function and its tangent line at the point. Use the tangent feature of the graphing utilitg.r to confirm your results. Determine the point at which the graph of the function below has a horizontal tangent line. [If the function has no horizontal tangent line, enter NONE.) y=x3+3x (HHS) Use the rules of differentiation to nd the derivative of the function. Determine the point at which the graph of the function below has a horizontal tangent line. [If the function has no horizontal tangent line, enter NONE.) _i YXz (HHS) Determine the point(s] (ifany) at which the graph of the function has a horizontal tangent line. (If the function has no horizontal tangent line, enter NONE.) y=x2+3 (w)=(:) Determine the point(s] (ifany) at which the graph of the function has a horizontal tangent line. (If the function has no horizontal tangent line, enter NONE.) 3x+ex y: (x,y)=( ) Determine the point(s] (ifany) at which the graph of the function has a horizontal tangent line. (If the function has no horizontal tangent line, enter NONE.) y=X+5ex (x,y)=( ) A silver dollar is dropped from the top of a building that is 1362 feet tall. Use the position function below for free-falling objects. s(t) = -16tz + Vat + 50 (a) Determine the position and velocity functions for the coin. s(t) = V(t) = (b) Determine the average velocity on the interval [1, 2]. ft/5 (c) Find the instantaneous velocities when t = 1 second and t = 2 seconds. V(1) = ft/s V(2) = ft/s (d) Find the time required for the coin to reach the ground level. (Round your answer to three decimal places.) t = S (e) Find the velocity of the coin at impact. (Round your answer to three decimal places.) ft/sA ball is thrown straight down from the top of a 476-foot building with an initial velocityr of -19 feet per second. Use the position function below for free-falling objects. __ 2 s(t) 16: +v0t+so What is its velocity after 3 seconds? 3) =Em What is its velocity after falling 332 feet? v=:m Use the rules of differentiation to find the derivative of the function. g(x) = 9x + 3 g'(x) =Use the rules of differentiation to find the derivative of the function. f(t) = -6t2 - 8t + 1 F ' (t ) =Use the rules of differentiation to nd the derivative of the function. s(f)=t3+8t27t+5 Use the rules of differentiation to nd the derivative of the function. 1': . =_5In|9 y 5 () Use the rules of differentiation to find the derivative of the function. 2 coS(X) =