Hi i need help with the following question please answer all the question is an extension im looking for 2.2 answers please

The fist question and answer

Thank you

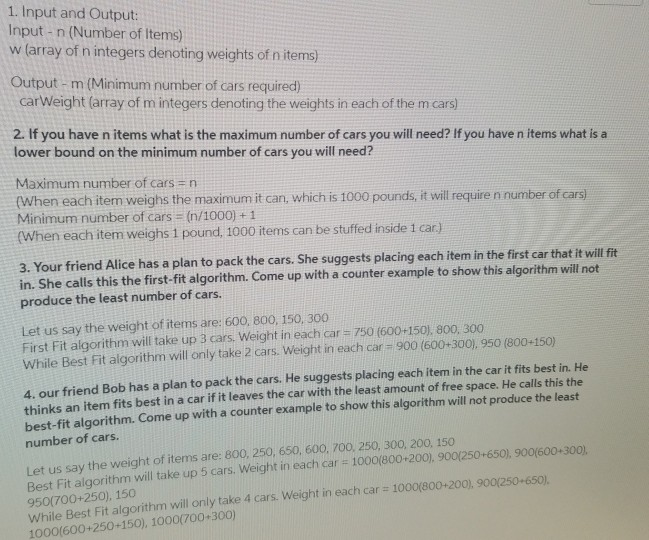
2.2 EXPLORE Consider the Job Selection problem from lecture. You will modify the solution to this problem to work for a related problem. In lecture we had the rule that if you work one day you can't work the next (or previous). In the modified problem you are allowed to work two days in a row but not three days in a row (so if you work 2 days in a row you can't work the day before these 2 days or the day after). 1. (2 point) Express the modified problem formally with input and output conditions. 2 2. (4 points) State a self-reduction for your problem. Use the self-reduction from lecture as inspiration 3. (4 points) Give pseudocode for a dynamic programming algorithm based off of your self reduction that computes the maximum earnings. 4. (4 points) Design a function that recovers the days that must be worked to achieve the maximum earnings. 5. (4 point) Compute the maximum earnings and the days to work for this input (same as above). P = 15,9,12,7,5, 13,7,5,4,9,8.7,5,8,4,3,5,10,4,6,8,12,5,6,3,7,16,2,2, 16 6. (2 points) What are the worst case time and space requirements of your complete solution? 2.1 UNDERSTAND 1. (3 points) Let F; be the ith Fibonacci number such that Fo = 0 and Fi = 1. Use the dynamic programming solution to compute F20. Show your work. 2. (3 points) Consider the Job Selection problem from lecture. Compute the optimal set of jobs and the maximum earnings for the following input. P = [5,9,12,7,5,13,7,5,4,9,8,7,5,8,4,3,5,10,4,6,8,12,5,6,3,7,16,2,2,16] 3. You and your friends are driving to Tijuana for spring break. You discover that you are bringing a lot of gear, luggage, and people and may have to take multiple cars. You have n items you want to bring. Each item weighs between 1 pound and 1000 pounds. Each car can hold at most 1000 pounds. You want to determine how to assign items to cars so that you use the minimum number of cars. a) (3 points) State the input and output conditions for this problem as precisely as possible. b) (3 points) If you have n items what is the maximum number of cars you will need? If you have n items what is a lower bound on the minimum number of cars you will need? c) (4 points) Your friend Alice has a plan to pack the cars. She suggests placing each item in the first car that it will fit in. She calls this the first-fit algorithm. Come up with a counter example to show this algorithm will not produce the least number of cars. (4 points) Your friend Bob has a plan to pack the cars. He suggests placing each item in the car it fits best in. He thinks an item fits best in a car if it leaves the car with the least amount of free space. He calls this the best-fit algorithm. Come up with a counter example to show this algorithm will not produce the least number of cars. 1. Input and Output: Input - n (Number of Items) w (array of n integers denoting weights of n items) Output - m (Minimum number of cars required) car Weight (array of m integers denoting the weights in each of the m cars) 2. If you have n items what is the maximum number of cars you will need? If you have n items what is a lower bound on the minimum number of cars you will need? Maximum number of cars = n (When each item weighs the maximum it can, which is 1000 pounds, it will require n number of cars) Minimum number of cars = (n/1000) + 1 (When each item weighs 1 pound, 1000 items can be stuffed inside 1 car) 3. Your friend Alice has a plan to pack the cars. She suggests placing each item in the first car that it will fit in. She calls this the first-fit algorithm. Come up with a counter example to show this algorithm will not produce the least number of cars. Let us say the weight of items are: 600, 800, 150, 300 First Fit algorithm will take up 3 cars. Weight in each car = 750 (600+150). 800, 300 While Best Fit algorithm will only take 2 cars. Weight in each car = 900 (600+300), 950 (800+150) 4. our friend Bob has a plan to pack the cars. He suggests placing each item in the car it fits best in. He thinks an item fits best in a car if it leaves the car with the least amount of free space. He calls this the best-fit algorithm. Come up with a counter example to show this algorithm will not produce the least number of cars. Let us say the weight of items are: 800, 250, 650, 600, 700, 250, 300, 200, 150 Best Fit algorithm will take up 5 cars. Weight in each car = 1000(800+200), 900(250-650), 900(600-300). 950(700+250), 150 While Best Fit algorithm will only take 4 cars. Weight in each car = 1000(800+200), 900(250-650). 1000(600+250-150), 1000(700-300) 2.2 EXPLORE Consider the Job Selection problem from lecture. You will modify the solution to this problem to work for a related problem. In lecture we had the rule that if you work one day you can't work the next (or previous). In the modified problem you are allowed to work two days in a row but not three days in a row (so if you work 2 days in a row you can't work the day before these 2 days or the day after). 1. (2 point) Express the modified problem formally with input and output conditions. 2 2. (4 points) State a self-reduction for your problem. Use the self-reduction from lecture as inspiration 3. (4 points) Give pseudocode for a dynamic programming algorithm based off of your self reduction that computes the maximum earnings. 4. (4 points) Design a function that recovers the days that must be worked to achieve the maximum earnings. 5. (4 point) Compute the maximum earnings and the days to work for this input (same as above). P = 15,9,12,7,5, 13,7,5,4,9,8.7,5,8,4,3,5,10,4,6,8,12,5,6,3,7,16,2,2, 16 6. (2 points) What are the worst case time and space requirements of your complete solution? 2.1 UNDERSTAND 1. (3 points) Let F; be the ith Fibonacci number such that Fo = 0 and Fi = 1. Use the dynamic programming solution to compute F20. Show your work. 2. (3 points) Consider the Job Selection problem from lecture. Compute the optimal set of jobs and the maximum earnings for the following input. P = [5,9,12,7,5,13,7,5,4,9,8,7,5,8,4,3,5,10,4,6,8,12,5,6,3,7,16,2,2,16] 3. You and your friends are driving to Tijuana for spring break. You discover that you are bringing a lot of gear, luggage, and people and may have to take multiple cars. You have n items you want to bring. Each item weighs between 1 pound and 1000 pounds. Each car can hold at most 1000 pounds. You want to determine how to assign items to cars so that you use the minimum number of cars. a) (3 points) State the input and output conditions for this problem as precisely as possible. b) (3 points) If you have n items what is the maximum number of cars you will need? If you have n items what is a lower bound on the minimum number of cars you will need? c) (4 points) Your friend Alice has a plan to pack the cars. She suggests placing each item in the first car that it will fit in. She calls this the first-fit algorithm. Come up with a counter example to show this algorithm will not produce the least number of cars. (4 points) Your friend Bob has a plan to pack the cars. He suggests placing each item in the car it fits best in. He thinks an item fits best in a car if it leaves the car with the least amount of free space. He calls this the best-fit algorithm. Come up with a counter example to show this algorithm will not produce the least number of cars. 1. Input and Output: Input - n (Number of Items) w (array of n integers denoting weights of n items) Output - m (Minimum number of cars required) car Weight (array of m integers denoting the weights in each of the m cars) 2. If you have n items what is the maximum number of cars you will need? If you have n items what is a lower bound on the minimum number of cars you will need? Maximum number of cars = n (When each item weighs the maximum it can, which is 1000 pounds, it will require n number of cars) Minimum number of cars = (n/1000) + 1 (When each item weighs 1 pound, 1000 items can be stuffed inside 1 car) 3. Your friend Alice has a plan to pack the cars. She suggests placing each item in the first car that it will fit in. She calls this the first-fit algorithm. Come up with a counter example to show this algorithm will not produce the least number of cars. Let us say the weight of items are: 600, 800, 150, 300 First Fit algorithm will take up 3 cars. Weight in each car = 750 (600+150). 800, 300 While Best Fit algorithm will only take 2 cars. Weight in each car = 900 (600+300), 950 (800+150) 4. our friend Bob has a plan to pack the cars. He suggests placing each item in the car it fits best in. He thinks an item fits best in a car if it leaves the car with the least amount of free space. He calls this the best-fit algorithm. Come up with a counter example to show this algorithm will not produce the least number of cars. Let us say the weight of items are: 800, 250, 650, 600, 700, 250, 300, 200, 150 Best Fit algorithm will take up 5 cars. Weight in each car = 1000(800+200), 900(250-650), 900(600-300). 950(700+250), 150 While Best Fit algorithm will only take 4 cars. Weight in each car = 1000(800+200), 900(250-650). 1000(600+250-150), 1000(700-300)