Hi, need help for the statistics. It will be very appreciated if you are able to show the calculation!!! Thank you so much!!

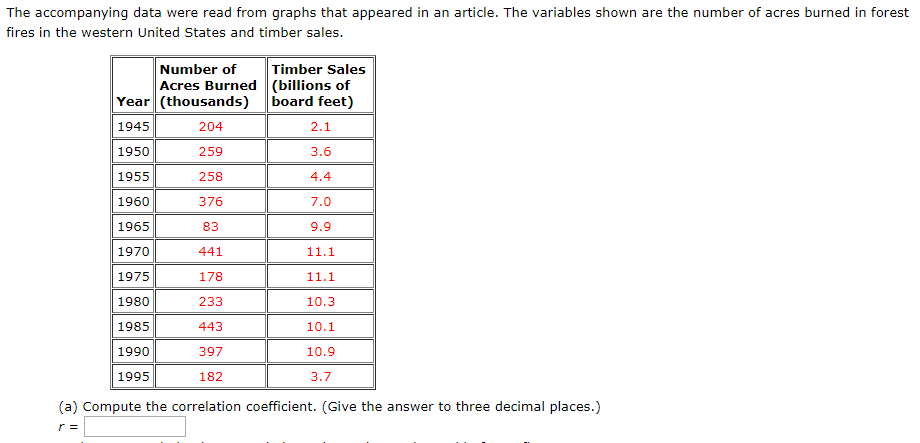
A store sells two different brands of dishwasher soap, and each brand comes in three different sizes: small {5), medium {M}, and large {L}. The proportions of the two brands and of the three sizes purchased are displayed as marginal totals in the table. Suppose that any event involving brand is independent of any event involving size. I.\"u'hat is the probability of the event that a randomly selected purchaser buys the small size of Brand B] {the event 8105}? What are the probabilities of the other brandsize combinations? (Fill up the table.) BrandiE E VIIHf ml || 0.?0 || 0.10 W 0.20 A friend who works in a big city owns two cars, one small and one large. One-quarter of the time he drives the small car to work, and three-quarters of the time he takes the large car. If he takes the small car, he usually has little trouble parking and so is at work on time with probability 0.8. If he takes the large car, he is on time to work with probability 0.5. Given that he was at work on time on a particular morning, what is the probability that he drove the small car? (Give the answer to three decimal places.) |:| There are two traffic lights on the route used by a certain individual to go from home to work. Let E denote the event that the individual must stop at the first light, and define the event F in a similar manner for the second light. Suppose that P(E) = 0.3, P(F) = 0.2, and P(E n F) = 0.15. (a) What is the probability that the individual must stop at at least one light; that is, what is the probability of the event P(E U F)? (b) What is the probability that the individual doesn't have to stop at either light? (c) What is the probability that the individual must stop at exactly one of the two lights? (d) What is the probability that the individual must stop just at the first light? (Hint: How is the probability of this event related to P(E) and P(E () F)? A Venn diagram might help.)A construction firm bids on two different contracts. Let E1 be the event that the bid on the first contract is successful, and define E2 analogously for the second contract. Suppose that P(61) = 0.2 and P(62) = 0.3 and that E1 and Ez are independent events. (a) Calculate the probability that both bids are successful (the probability of the event E1 and E2). (b) Calculate the probability that neither bid is successful (the probability of the event (not E1) and (not E2)). (c) What is the probability that the firm is successful in at least one of the two bids?The accompanying data were read from graphs that appeared in an article. The variables shown are the number of acres burned in forest fires in the western United States and timber sales. Number of Timber Sales Acres Burned (billions of Year (thousands) board feet) 1945 204 2.1 1950 259 3.6 1955 258 4.4 1960 376 7.0 1965 83 9.9 1970 441 11.1 1975 178 11.1 1980 233 10.3 1985 443 10.1 1990 397 10.9 1995 182 3.7 (a) Compute the correlation coefficient. (Give the answer to three decimal places.) r=