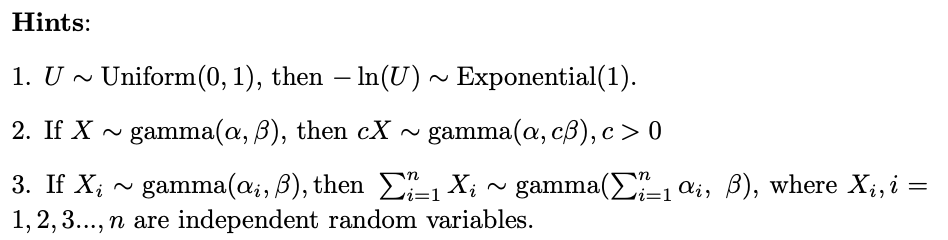
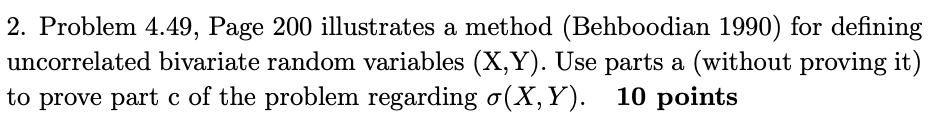
Hints: 1. U N Uniform(0,1), then 111(U) ~ Exponential). 2. If X N gamma.(a, )8), then (:X N gamma(a, 0,8), (3 > 0 3. If Xi ~ gamma(a,,8),then 2:\":1 X,; N gamma(z?=l (11;, [3), where Xhi = 1, 2, 3..., n are independent random variables. 2. Problem 4.49, Page 200 illustrates a method (Behboodian 1990) for defining uncorrelated bivariate random variables (X,Y). Use parts a (without proving it) to prove part c of the problem regarding o (X, Y). 10 pointsBehboodian (1990) illustrates how to construct bivariate random variables that are uncorrelated but dependent. Suppose that f1, f2, 91, 92 are univariate densities with means /1, /2, $1, $2, respectively, and the bivariate random variable (X, Y ) has density (X, Y) ~afi(x)gi(y) + (1 -a) f2(2) 92(y), where 0