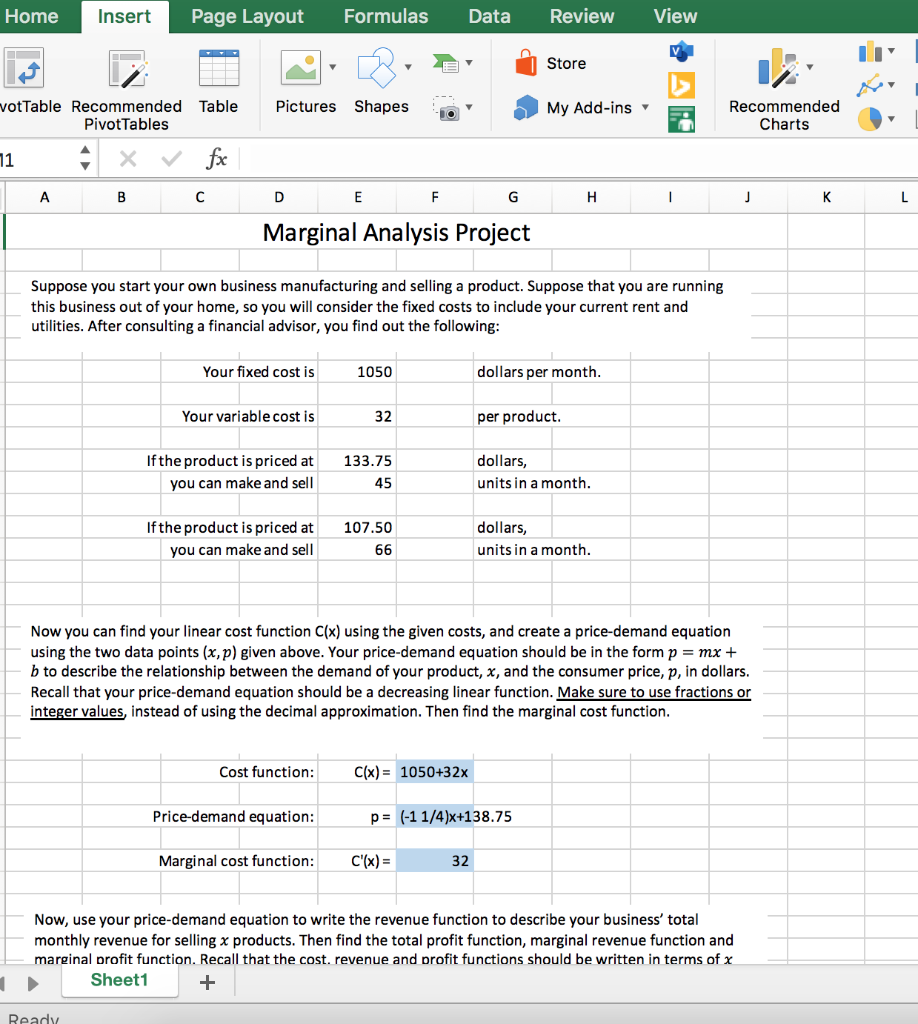
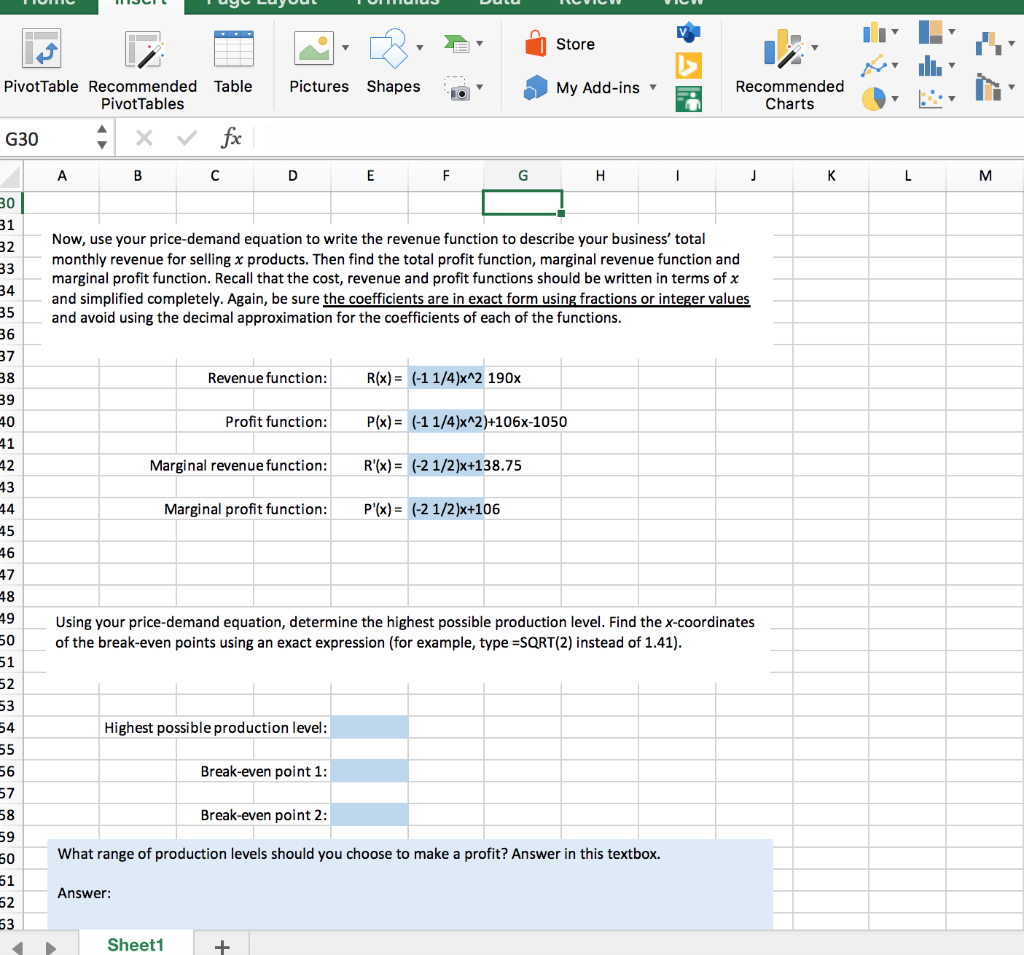
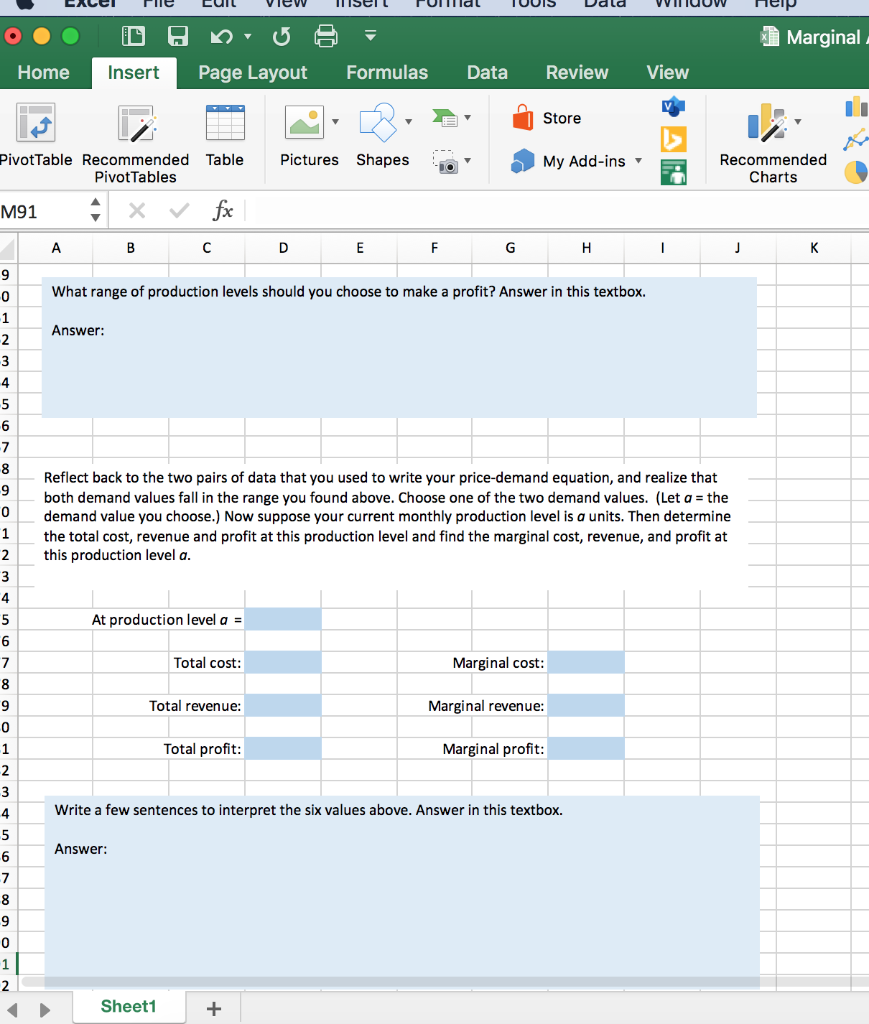
Home Insert Page Layout Formulas Data Review View Store v Pictures Shapes votTable Recommended Table Pivot Tables My Add-ins Recommended Charts 11 A x fx B D E F G H 1 J K L Marginal Analysis Project Suppose you start your own business manufacturing and selling a product. Suppose that you are running this business out of your home, so you will consider the fixed costs to include your current rent and utilities. After consulting a financial advisor, you find out the following: Your fixed cost is 1050 dollars per month. Your variable cost is 32 per product. If the product is priced at 133.75 dollars, you can make and sell 45 units in a month. 107.50 If the product is priced at you can make and sell dollars, units in a month. 66 Now you can find your linear cost function C(x) using the given costs, and create a price-demand equation using the two data points (x,p) given above. Your price-demand equation should be in the form p = mx + b to describe the relationship between the demand of your product, x, and the consumer price, p, in dollars. Recall that your price-demand equation should be a decreasing linear function. Make sure to use fractions or integer values instead of using the decimal approximation. Then find the marginal cost function. Cost function: C(x)= 1050+32x Price-demand equation: p= (-1 1/4)x+138.75 Marginal cost function: C'(x) = 32 Now, use your price-demand equation to write the revenue function to describe your business' total monthly revenue for selling x products. Then find the total profit function, marginal revenue function and marginal profit function. Recall that the cost. revenue and profit functions should be written in terms of x Sheet1 + Ready Store Pictures Shapes PivotTable Recommended Table Pivot Tables My Add-ins Recommended Charts G30 fox A B D E F G H 1 J L M 30 31 32 33 Now, use your price-demand equation to write the revenue function to describe your business' total monthly revenue for selling x products. Then find the total profit function, marginal revenue function and marginal profit function. Recall that the cost, revenue and profit functions should be written in terms of x and simplified completely. Again, be sure the coefficients are in exact form using fractions or integer values and avoid using the decimal approximation for the coefficients of each of the functions. 34 35 36 37 38 Revenue function: R(x)= (-1 1/4)x^2 190x 39 40 Profit function: P(x) = (-1 1/4)x^2)+106X-1050 41 42 Marginal revenue function: R'(x)= (-2 1/2)x+138.75 13 44 Marginal profit function: P'(x) = (-2 1/2)x+106 45 46 47 48 49 Using your price-demand equation, determine the highest possible production level. Find the x-coordinates of the break-even points using an exact expression (for example, type=SQRT(2) instead of 1.41). 50 51 52 53 54 Highest possible production level: 55 56 Break-even point 1: 57 58 Break-even point 2: 59 50 What range of production levels should you choose to make a profit? Answer in this textbox. 51 Answer: 52 63 Sheet1 + File CUIL View MISE Marginal Home Insert Page Layout Formulas Data Review View TE Store Pictures Shapes Pivot Table Recommended Table Pivot Tables My Add-ins TO Recommended Charts M91 fx A B D E F G H 1 j K 9 0 What range of production levels should you choose to make a profit? Answer in this textbox. 1 Answer: 2 3 4 5 6 7 8 9 0 Reflect back to the two pairs of data that you used to write your price-demand equation, and realize that both demand values fall in the range you found above. Choose one of the two demand values. (Let a = the demand value you choose.) Now suppose your current monthly production level is a units. Then determine the total cost, revenue and profit at this production level and find the marginal cost, revenue, and profit at this production level a. 1 2 3 4 5 At production level a = 6 7 Total cost: Marginal cost: 8 9 Total revenue: Marginal revenue: 0 1 Total profit: Marginal profit: 2 3 4 Write a few sentences to interpret the six values above. Answer in this textbox. 5 Answer: 6 7 8 9 0 1 2 Sheet1 + Home Insert Page Layout Formulas Data Review View Store v Pictures Shapes votTable Recommended Table Pivot Tables My Add-ins Recommended Charts 11 A x fx B D E F G H 1 J K L Marginal Analysis Project Suppose you start your own business manufacturing and selling a product. Suppose that you are running this business out of your home, so you will consider the fixed costs to include your current rent and utilities. After consulting a financial advisor, you find out the following: Your fixed cost is 1050 dollars per month. Your variable cost is 32 per product. If the product is priced at 133.75 dollars, you can make and sell 45 units in a month. 107.50 If the product is priced at you can make and sell dollars, units in a month. 66 Now you can find your linear cost function C(x) using the given costs, and create a price-demand equation using the two data points (x,p) given above. Your price-demand equation should be in the form p = mx + b to describe the relationship between the demand of your product, x, and the consumer price, p, in dollars. Recall that your price-demand equation should be a decreasing linear function. Make sure to use fractions or integer values instead of using the decimal approximation. Then find the marginal cost function. Cost function: C(x)= 1050+32x Price-demand equation: p= (-1 1/4)x+138.75 Marginal cost function: C'(x) = 32 Now, use your price-demand equation to write the revenue function to describe your business' total monthly revenue for selling x products. Then find the total profit function, marginal revenue function and marginal profit function. Recall that the cost. revenue and profit functions should be written in terms of x Sheet1 + Ready Store Pictures Shapes PivotTable Recommended Table Pivot Tables My Add-ins Recommended Charts G30 fox A B D E F G H 1 J L M 30 31 32 33 Now, use your price-demand equation to write the revenue function to describe your business' total monthly revenue for selling x products. Then find the total profit function, marginal revenue function and marginal profit function. Recall that the cost, revenue and profit functions should be written in terms of x and simplified completely. Again, be sure the coefficients are in exact form using fractions or integer values and avoid using the decimal approximation for the coefficients of each of the functions. 34 35 36 37 38 Revenue function: R(x)= (-1 1/4)x^2 190x 39 40 Profit function: P(x) = (-1 1/4)x^2)+106X-1050 41 42 Marginal revenue function: R'(x)= (-2 1/2)x+138.75 13 44 Marginal profit function: P'(x) = (-2 1/2)x+106 45 46 47 48 49 Using your price-demand equation, determine the highest possible production level. Find the x-coordinates of the break-even points using an exact expression (for example, type=SQRT(2) instead of 1.41). 50 51 52 53 54 Highest possible production level: 55 56 Break-even point 1: 57 58 Break-even point 2: 59 50 What range of production levels should you choose to make a profit? Answer in this textbox. 51 Answer: 52 63 Sheet1 + File CUIL View MISE Marginal Home Insert Page Layout Formulas Data Review View TE Store Pictures Shapes Pivot Table Recommended Table Pivot Tables My Add-ins TO Recommended Charts M91 fx A B D E F G H 1 j K 9 0 What range of production levels should you choose to make a profit? Answer in this textbox. 1 Answer: 2 3 4 5 6 7 8 9 0 Reflect back to the two pairs of data that you used to write your price-demand equation, and realize that both demand values fall in the range you found above. Choose one of the two demand values. (Let a = the demand value you choose.) Now suppose your current monthly production level is a units. Then determine the total cost, revenue and profit at this production level and find the marginal cost, revenue, and profit at this production level a. 1 2 3 4 5 At production level a = 6 7 Total cost: Marginal cost: 8 9 Total revenue: Marginal revenue: 0 1 Total profit: Marginal profit: 2 3 4 Write a few sentences to interpret the six values above. Answer in this textbox. 5 Answer: 6 7 8 9 0 1 2 Sheet1 +