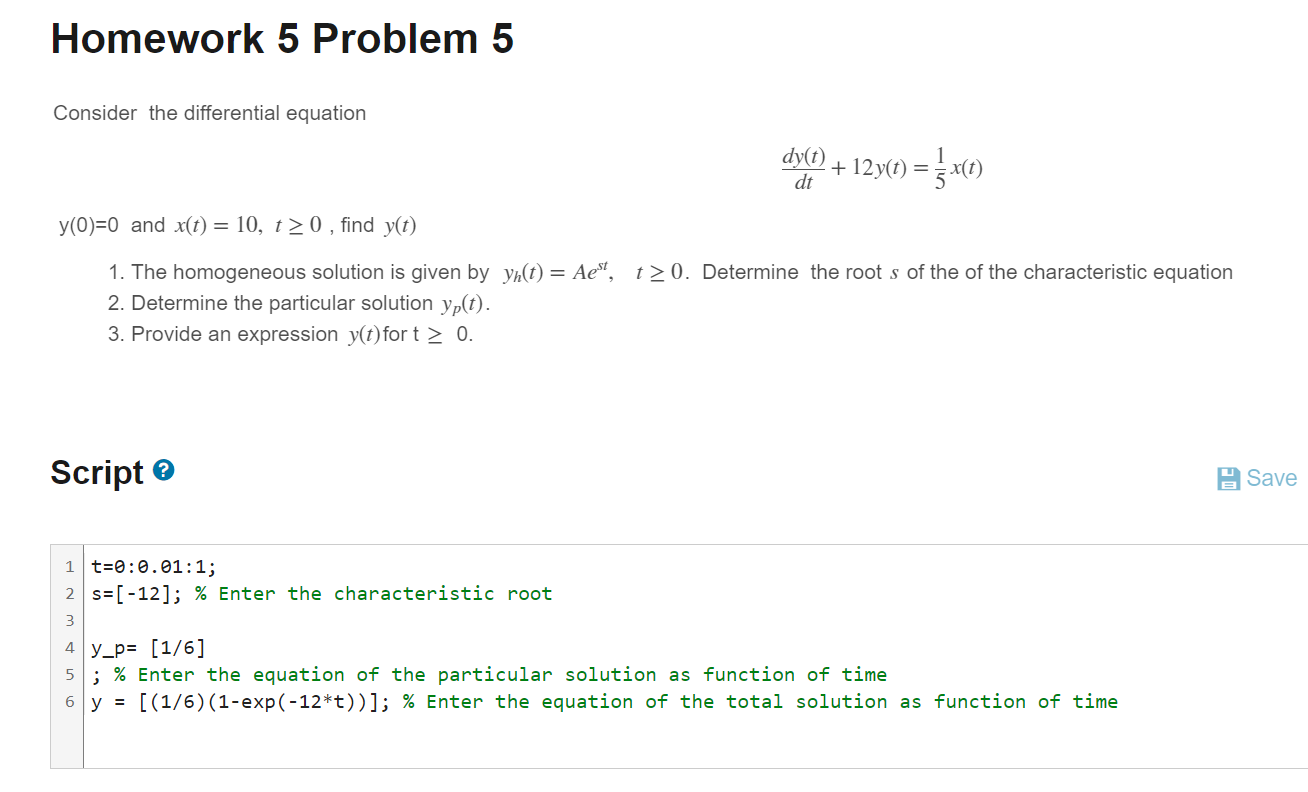
Homework 5 Problem 5 Consider the differential equation dy(t) dt 1 + 12y(r) = z x(1) | y(0)=0 and x(z) = 10, t > 0, find y(r) 1. The homogeneous solution is given by y, (1) = Ae\". > 0. Determine the root s of the of the characteristic equation 2. Determine the particular solution y,(7). 3. Provide an expression y(f)fort > 0. Script 1/t=0:0.01:1; 2 |s=[-12]; % Enter the characteristic root 3 4ly_p= [1/6] 5|; % Enter the equation of the particular solution as function of time 6|y = [(1/6)(1-exp(-12*t))]; % Enter the equation of the total solution as function of time