Homework: Modeling Applications

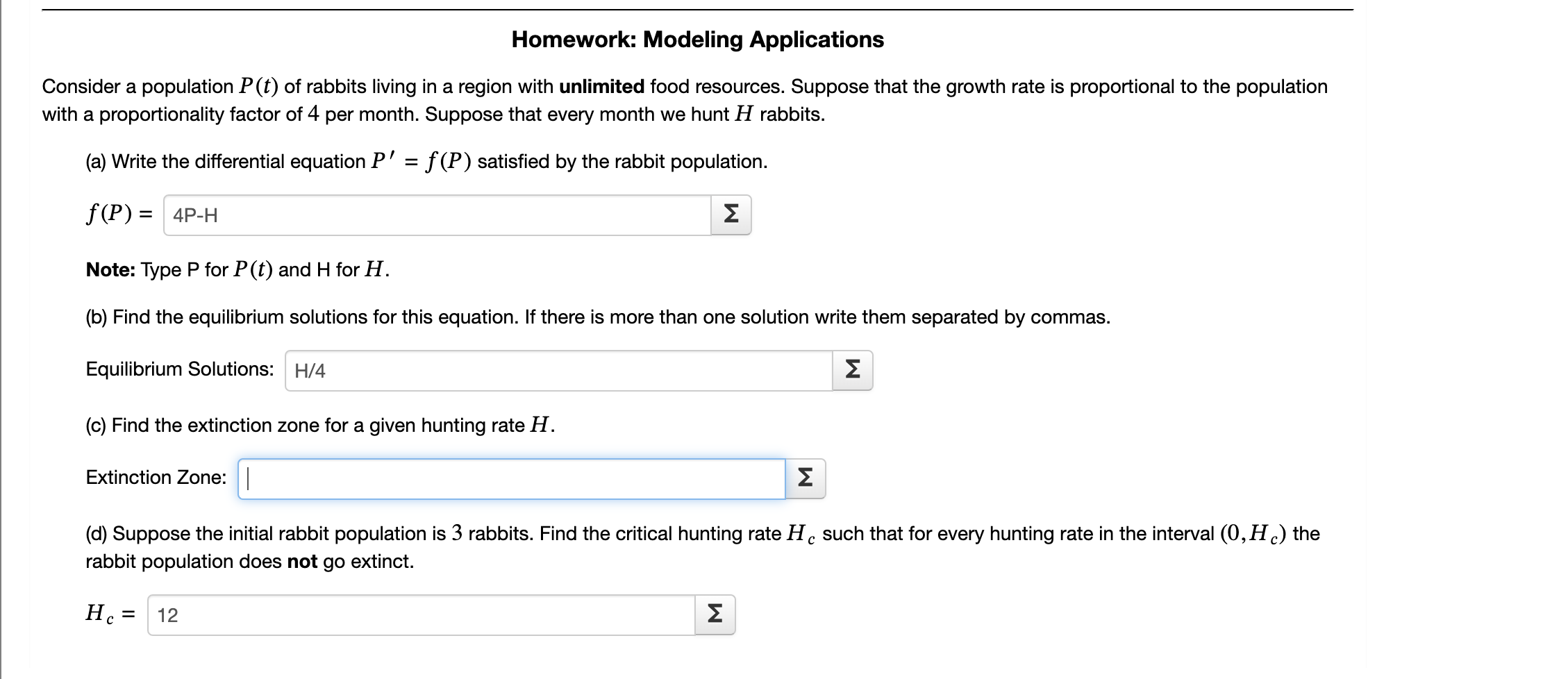
Consider a population $\backslash ($ P$($t$)\backslash )$ of rabbits living in a region with unlimited food resources. Suppose that the growth rate is proportional to the population with a proportionality factor of $4$ per month. Suppose that every month we hunt $\backslash ($ H $\backslash )$ rabbits.

$($a$)$ Write the differential equation $\backslash ($ P$^\{\backslash$prime$\}=$f$($P$)\backslash )$ satisfied by the rabbit population.

$\backslash [$

f$($P$)=$

$\backslash ]$

Note: Type P for $\backslash ($ P$($t$)\backslash )$ and H for $\backslash ($ H $\backslash ).$

$($b$)$ Find the equilibrium solutions for this equation. If there is more than one solution write them separated by commas.

Equilibrium Solutions:

$($c$)$ Find the extinction zone for a given hunting rate $\backslash ($ H $\backslash ).$

Extinction Zone:

$($d$)$ Suppose the initial rabbit population is $3$ rabbits. Find the critical hunting rate $\backslash ($ H$\_\{$c$\}\backslash )$ such that for every hunting rate in the interval $\backslash (\backslash$left$(0,$ H$\_\{$c$\}\backslash$right$)\backslash )$ the rabbit population does not go extinct.

$\backslash [$

H$\_\{$c$\}=$

$\backslash ]$