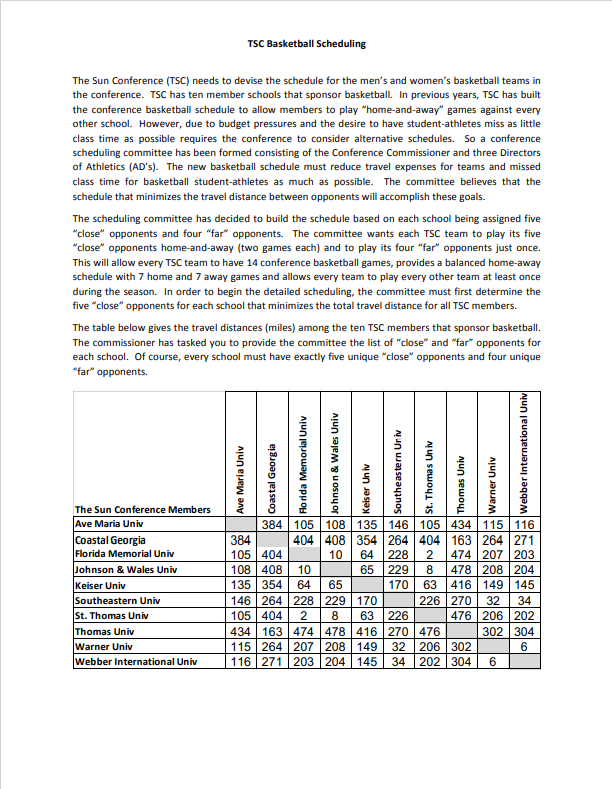
Question: How can this be solved using Linear Programming and Excel's Solver add-in? TSC Basketball Scheduling The Sun Conference (TSC) needs to devise the schedule for
How can this be solved using Linear Programming and Excel's Solver add-in?

Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


