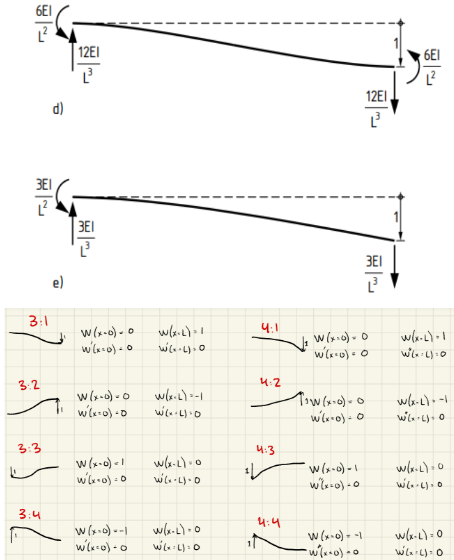
How do I derive the elementary cases for the displacement method? There are $4$ different solutions per case $(4$ different boundary conditions, se figure$).$

I have figured out the boundary conditions and the equations that are needed, but don't know how to get the results that are asked for $($including what the result even is for the other six boundary conditions where the directions should change, the ones that don't have the answer in the figure$).$

$(1)$EIw$=$Ax$+$B

$(2)$EIw$=(($Ax$^2)/2)+$Bx$+$C

$(3)$EIw$=(($Ax$^3)/6)+(($Bx$^2)/2)+$Cx$+$D

$(4)-$V$=$A

$(5)-$M$=$Ax$+$B