how do i fix it

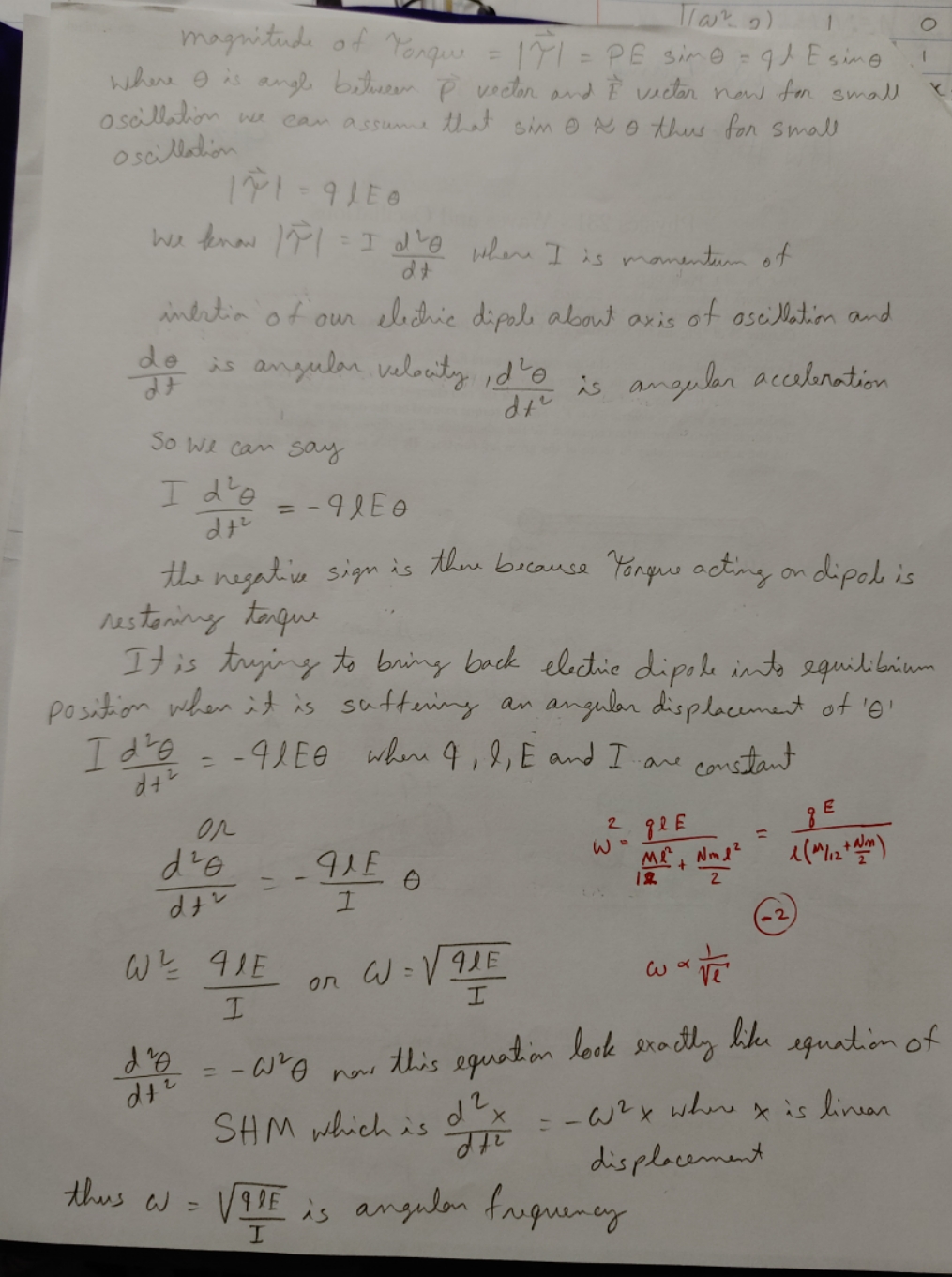
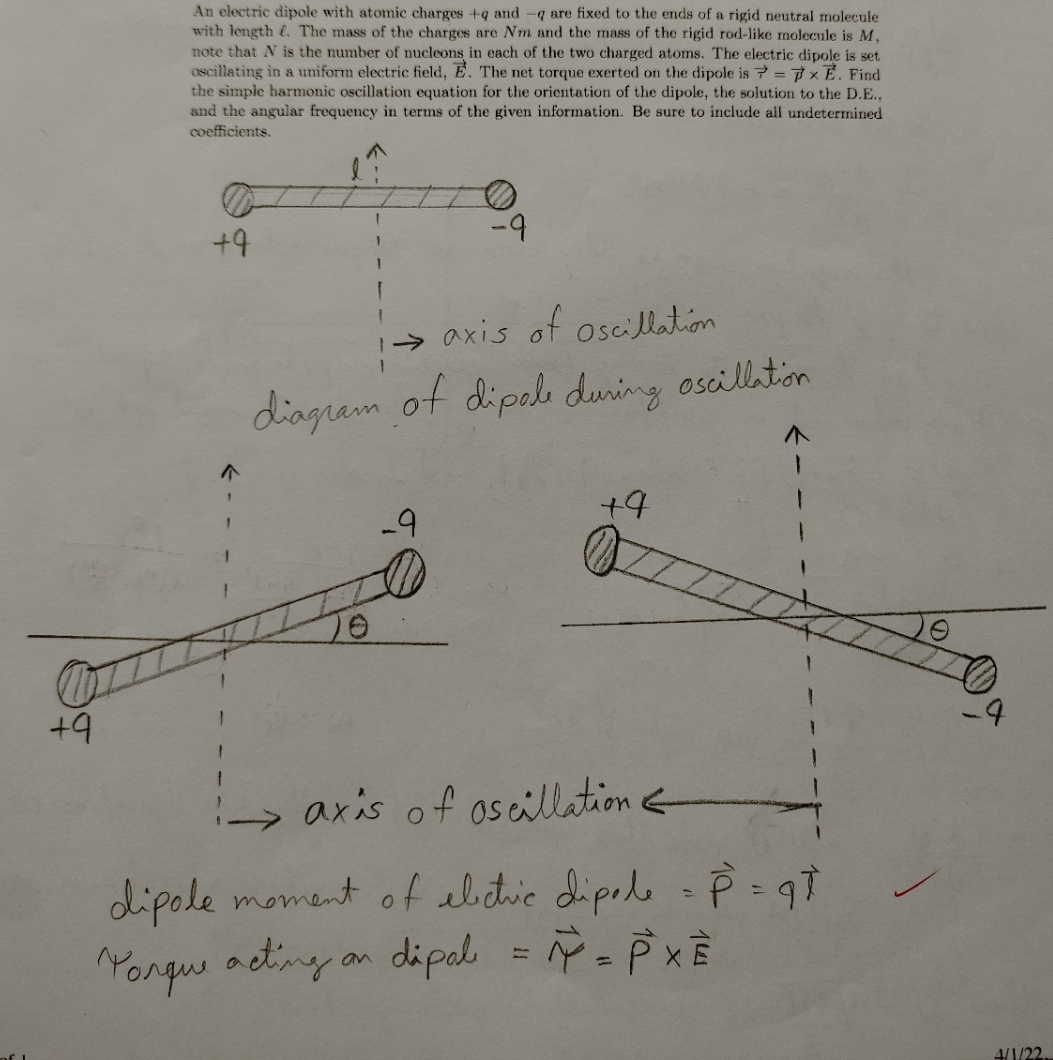
and the angular frequency coefficients. +4 - axis of oscillation into ase Nation . diagram of dipole during oscillation I ned = MLY Value of Omar and i depends on india I pay by mog roy Mon 4 9 about a aris passing through center of mass is So moment of invention of a particl of mass Am which is ble distance away from axis of notation is moment of imention of a nod of length lotmass M So moment of imention of two particles of mass Non and WIN 1-> axis of oscillation E dipole moment of electric dipole = P = 97 displacement of shootin Porque acting on dipal = 17 = PXE I de where I is momentum of inertia of our electric dipale about axis of oscillation and do is angular velocity ,d' is angular acceleration const - So we can say my MIOS Ide = - 91ED the negation sign is there because tongues acting on dipole is restoring tanque given old ) ( the value ) 6 ( 1 1 / w cos( utter ) ( 1 + q m ) wis = (710 It is trying to bring back elective dipole into equilibrium act ) - Emmy Sin( wit + ( ) 12 ( ~ / CH1 8 ) + (H8 = Wax position when it is stuttering an angular displacement of 's I die =- 91EQ when 4, 9, E and I are constant On armin + 1 w I : pimp to promout myof of OH ) = 0 mamy sin (out ter ) + 0mm cos ? ( wit the ) (-2) = fand if teo or Like o(t .. ) I one can solve even if t to . dit =- GO now this equation look exactly like equation of SHM which is d 2 x : - wax where &is linean displacement theis a = VIDE is angular frequencymagnitude of Yongw = 171 = PE sime = 91 Esing where I is and between P vector and E victor new for small oscillation we can assume that sim A thus for small oscillation 171 - 91 EO we kenaw /71 : I d' when I is momentum of inertia of our electric dipole about axis of oscillation and do is angular velocity, die die is angular acceleration so we can say I d's dic = - 9lE0 the negative sign is there because torque acting on dipole is restoring teague It is trying to bring back elective dipole into equilibrium position when it is suffering an angular displacement of 's I dro JAr = - TREG when 9, 9, E and I are constant Or 2 gRE 8 E W . MR" * Nm 1 2 1 ( M / 12 + Wm ) 18 2 I - 2 I I die 142 = - W'D now this equation look exactly like equation of SHM which is d2 x dic = - wax where x is linear displacement this w = VAPE is angular frequency IAn electric dipole with atomic charges +q and -q are fixed to the ends of a rigid neutral molecule with length . The mass of the charges are Am and the mass of the rigid rod-like molecule is M, note that N is the number of nucleons in each of the two charged atoms. The electric dipole is set oscillating in a uniform electric field, E. The net torque exerted on the dipole is ? = # x E. Find the simple harmonic oscillation equation for the orientation of the dipole, the solution to the D.E., coefficients. and the angular frequency in terms of the given information. Be sure to include all undetermined +9 1 -> axis of oscillation diagram of dipole during oscillation - 7 9 +4 - - +9 - 4 i-> axis of oscillationE dipole moment of electric dipole = P = 97 Porque acting on dipali = ry = PXEand the general solution of this abow equation do - - who will be. TOmax = maximum angular displacement of electric O = 0 max sim ( WA + s ) dipole 8 = phase of aldie dipole Value of Away and I depends on initial conditions. It depends on how we are setting dipole into oscillation. Now we have to find I June Nm - - W 1 / 2 moment of inertia of a red of length lotmass M about an axis passing through center of mass is I ned = ML" Not INda 2 12 So moment of inertia of a particle of mass Nm which is I/2 distance away from axis of notation is Ip = Nm / 1 / 2 ) 2 : Null J So moment of inertia of two particles of mass NM and both of them are 1/2 away from axis of notation will be 4/1/22 1:21 PIA = Ip + Ip - 2 Nmill _ Null N J So total moment of imention = I MIL N N Solve for Amman al ... ingeneral given Olt ) ( The value ) Oct ) - Emax sin ( wit + u ) Like B (t :. ) @ (t =0 ) dole ) = w emmy cos ( art tu ) do ( t ) ( a value ) sin ( wt + 4 ) - + 0 a cos ( wt the )