How do I solve for this?

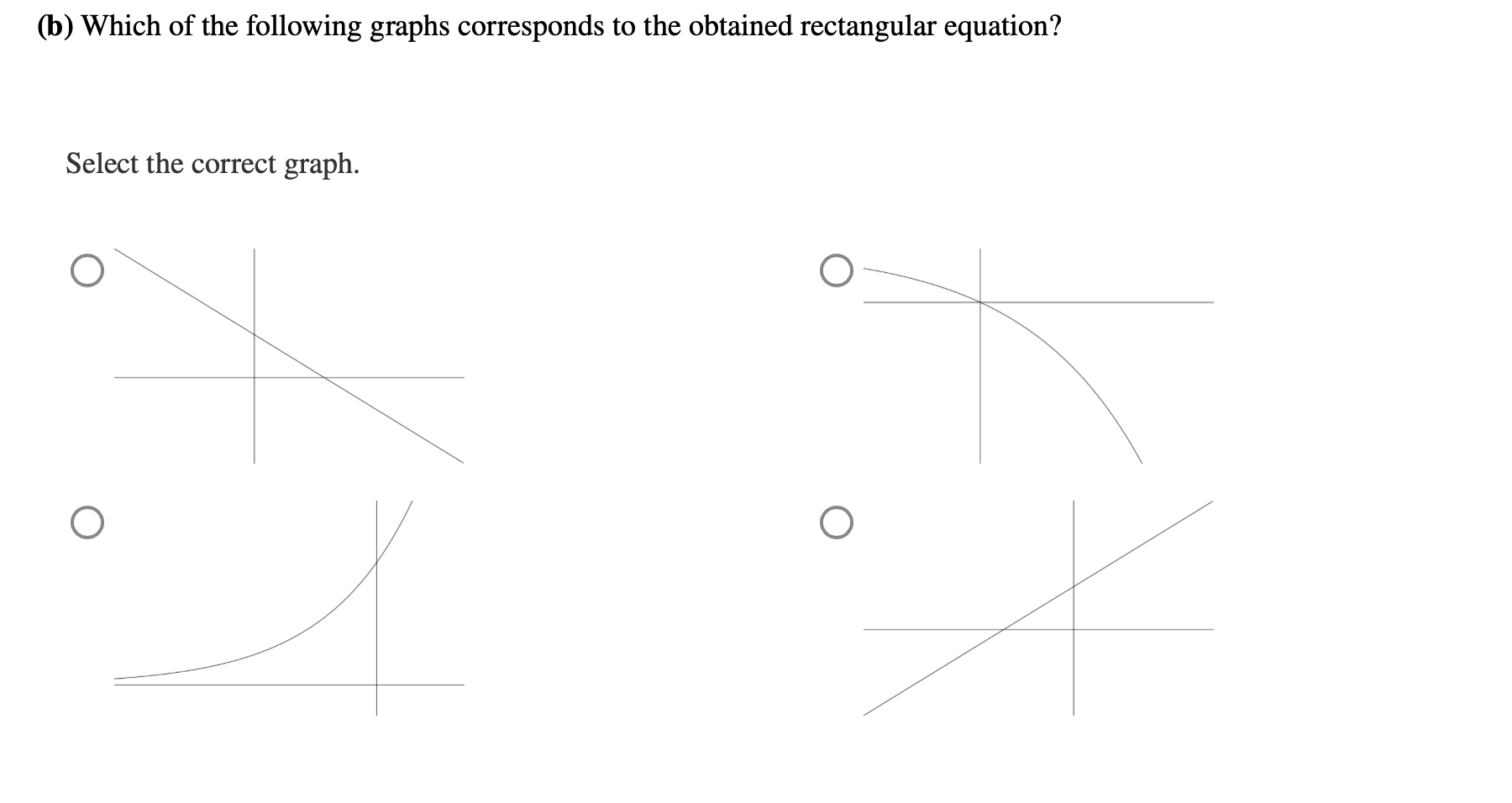
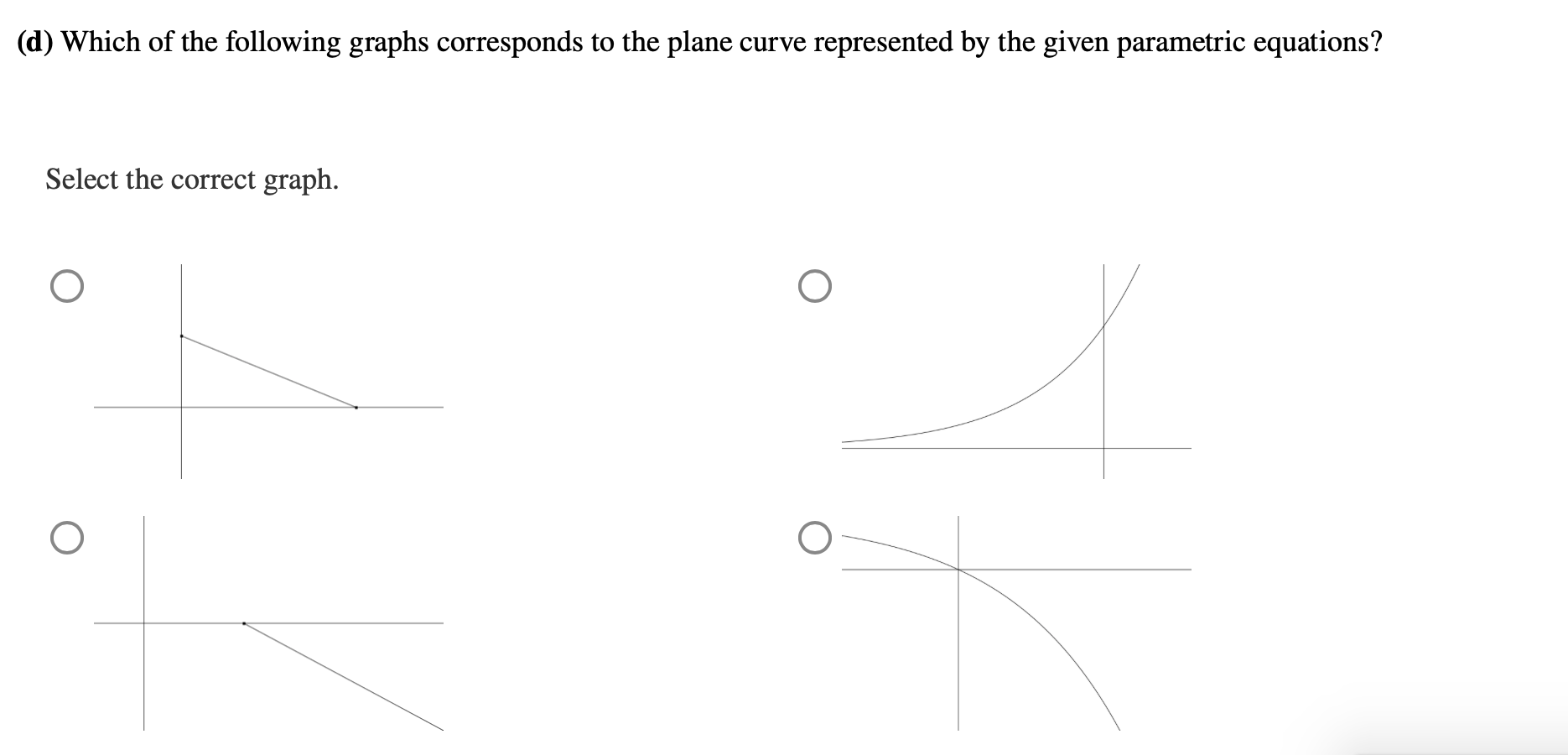
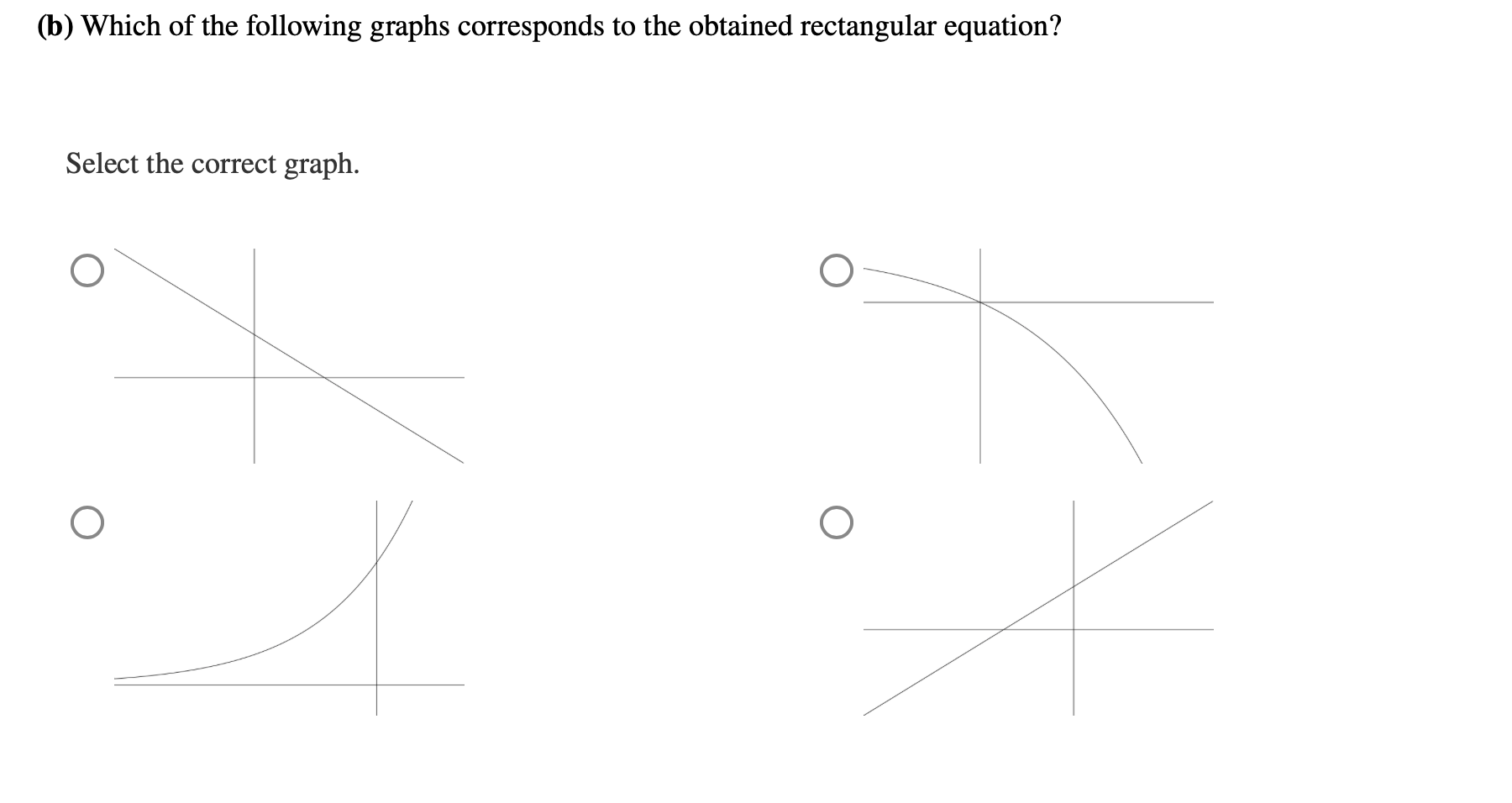
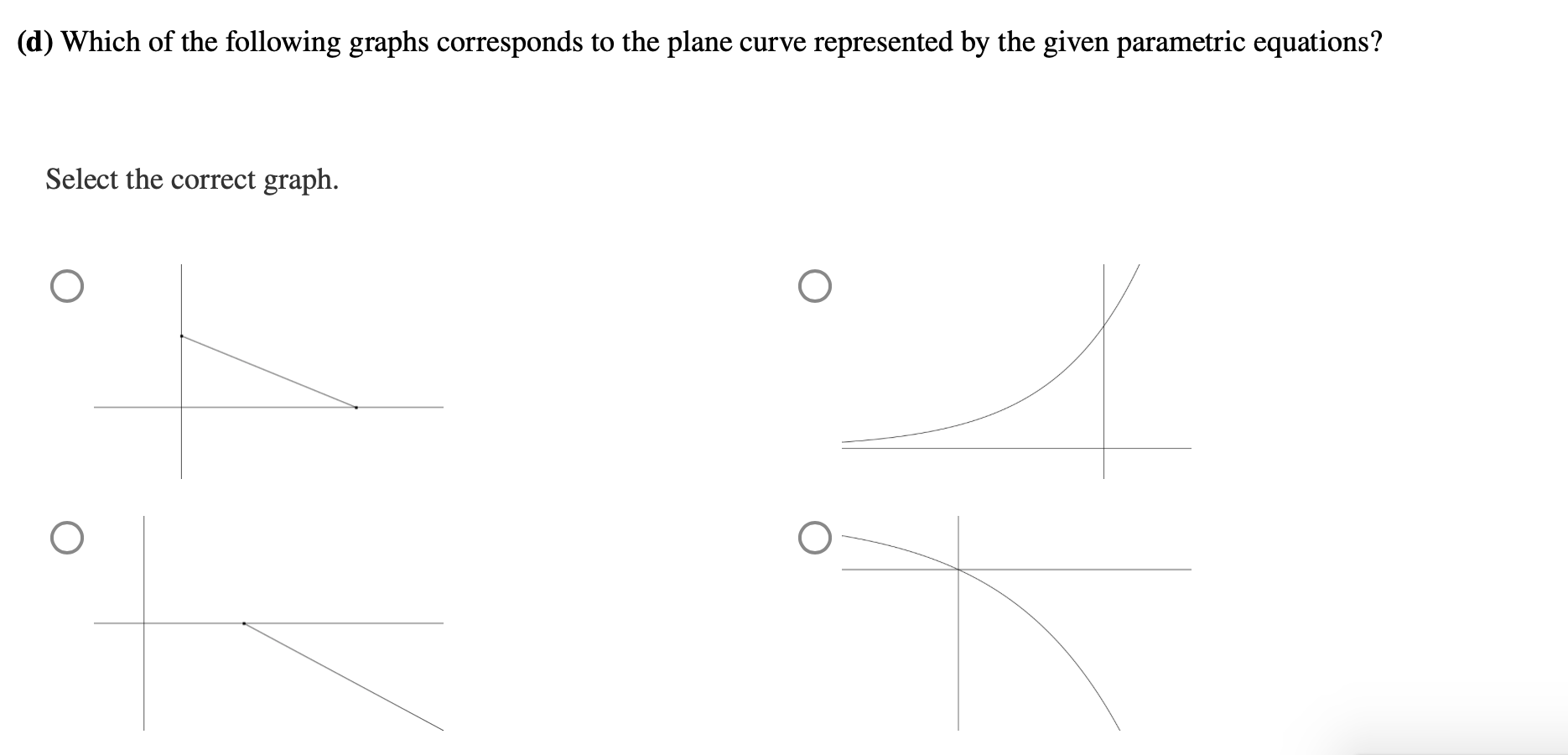
Consider the given parametric equations x(t) = Ze', y(t)=1 er; t2 0 (a) Find the rectangular equation of the plane curve with the given parametric equations. (Use symbolic notation and fractions where needed. Solve the rectangular equation for y in terms of x.) (b) Which of the following graphs corresponds to the obtained rectangular equation? Select the correct graph. 0 \\\\ O (c) Determine the restrictions on x and y so that the graph corresponding to the rectangular equation is identical to the plane curve. (Use symbolic notation and fractions Where needed. Give your answer as an interval in the form (*, *)_ Use the symbol 00 for innity, U for combining intervals, and an appropriate type of parentheses "(", ")", " ", or "]" depending on whether the interval is open or closed.) ((1) Which of the following graphs corresponds to the plane curve represented by the given parametric equations? Select the correct graph. 0 O Let x(t) = cos8 (7t), y(t) = sin8 (71'). Find ji. Assume dx 0. (Express numbers in exact form. Use symbolic notation and fractions where needed.) dx