How do I solve for this?

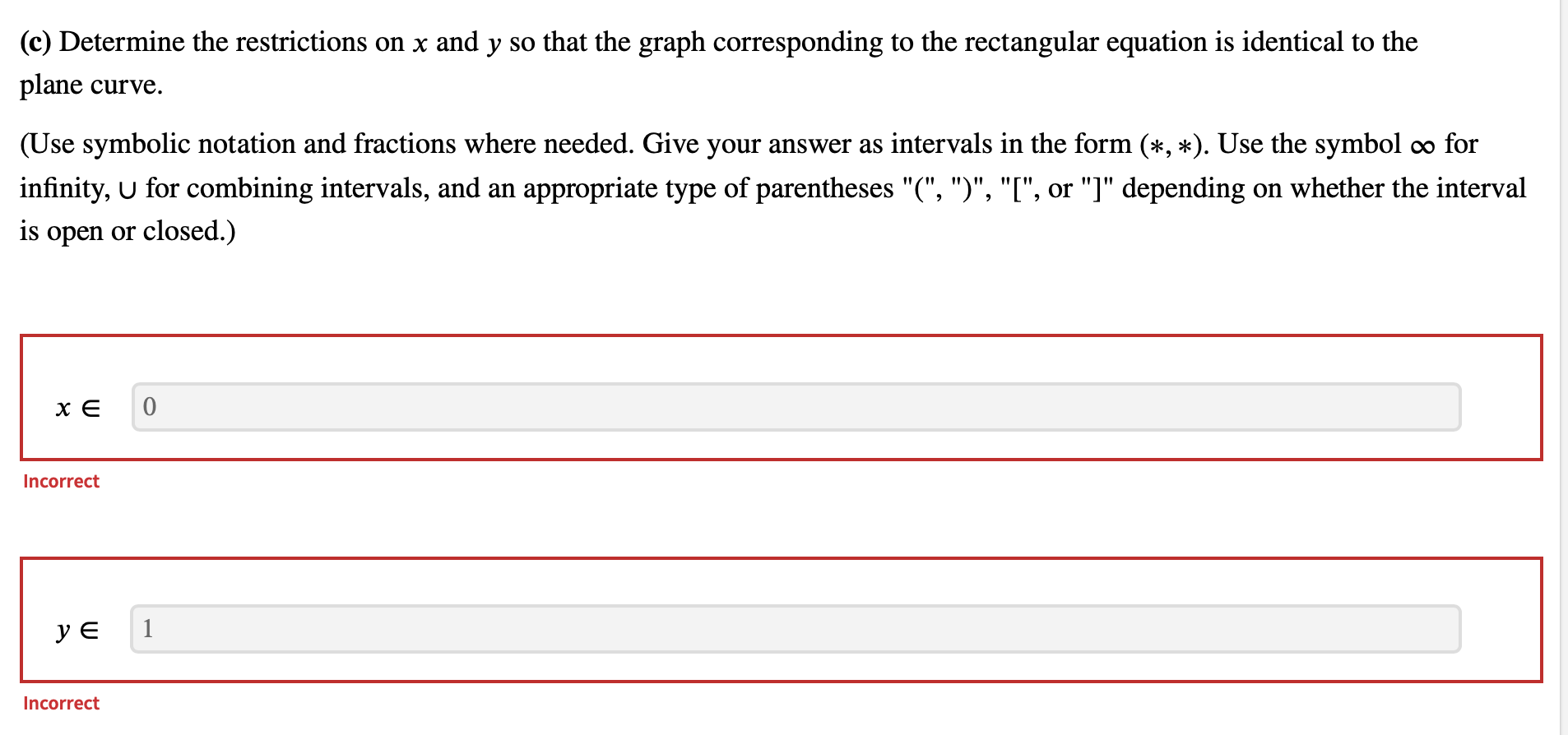
Consider the given parametric equations x(t) = 21,310) = t2+ 1; t > 0 (3) Find the rectangular equation of the plane curve with the given parametric equations. (Use symbolic notation and fractions where needed. Solve the rectangular equation for y in terms of x.) l 2 rectangular equation: Ex + 1 | n correct (b) Which of the following graphs corresponds to the rectangular equation? Select the correct graph. (c) Determine the restrictions on x and y so that the graph corresponding to the rectangular equation is identical to the plane curve. (Use symbolic notation and fractions where needed. Give your answer as intervals in the form (*, *). Use the symbol 00 for innity, U for combining intervals, and an appropriate type of parentheses "(", ")", " [", or "]" depending on Whether the interval is open or closed.) (c) Determine the restrictions on x and y so that the graph corresponding to the rectangular equation is identical to the plane curve. (Use symbolic notation and fractions where needed. Give your answer as intervals in the form (as, 21:). Use the symbol 00 for innity, U for combining intervals, and an appropriate type of parentheses "(", ")", " [", or "]" depending on whether the interval is open or closed.) x6 0 l n co rrect ye 1 | n co rrect