How do I solve the second part to this question?

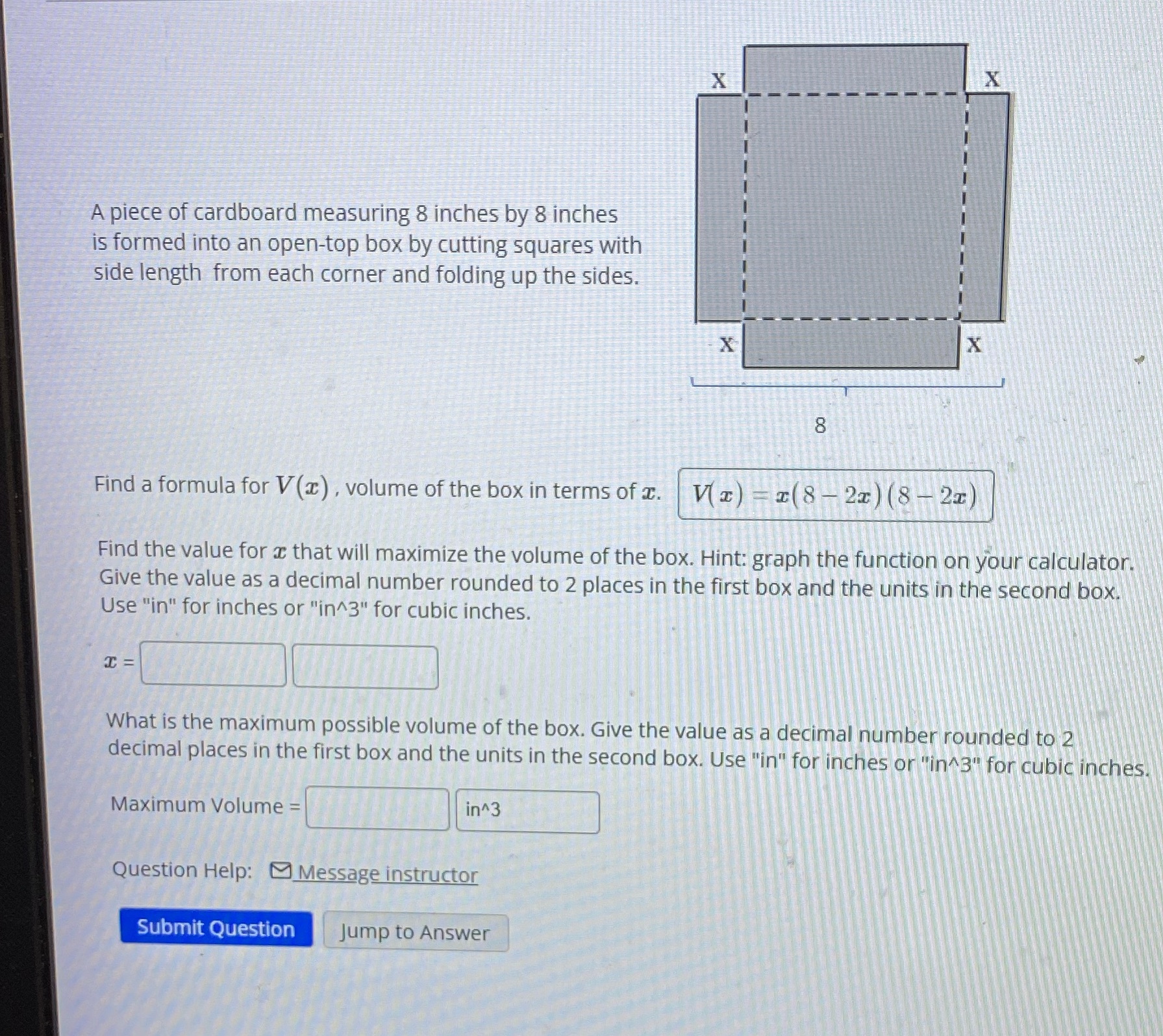
A piece of cardboard measuring 8 inches by 8 inches is formed into an open-top box by cutting squares with side length from each corner and folding up the sides. X DO Find a formula for V(x) , volume of the box in terms of I. VI) = 1(8 - 21) (8- 21) Find the value for a that will maximize the volume of the box. Hint: graph the function on your calculator. Give the value as a decimal number rounded to 2 places in the first box and the units in the second box. Use "in" for inches or "in^3" for cubic inches. What is the maximum possible volume of the box. Give the value as a decimal number rounded to 2 decimal places in the first box and the units in the second box. Use "in" for inches or "in 3" for cubic inches. Maximum Volume in^3 Question Help: Message instructor Submit Question Jump to