Question: How do I solve these? Select the big-Oh characterization, in terms of n, for the following loop. s=0fori=1ton2doforj=1toidos=s+i O(n2) O(nlogn) O(n4) O(n3) O(2n) O(1) O(n)
How do I solve these?
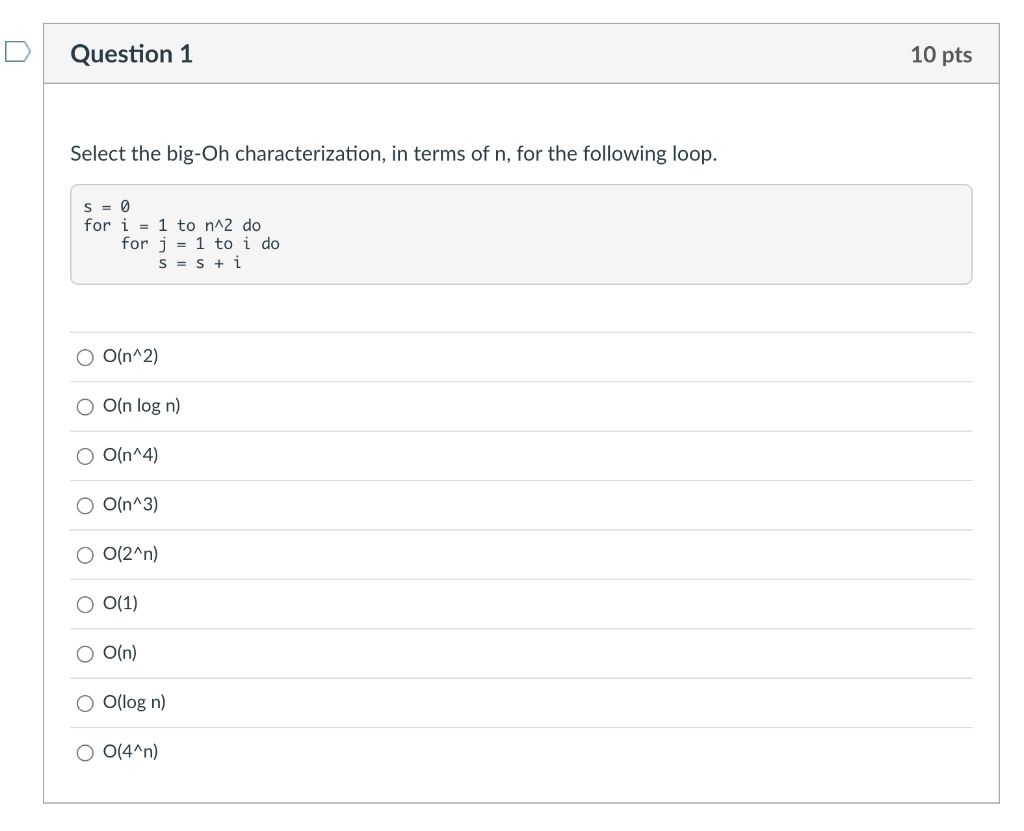
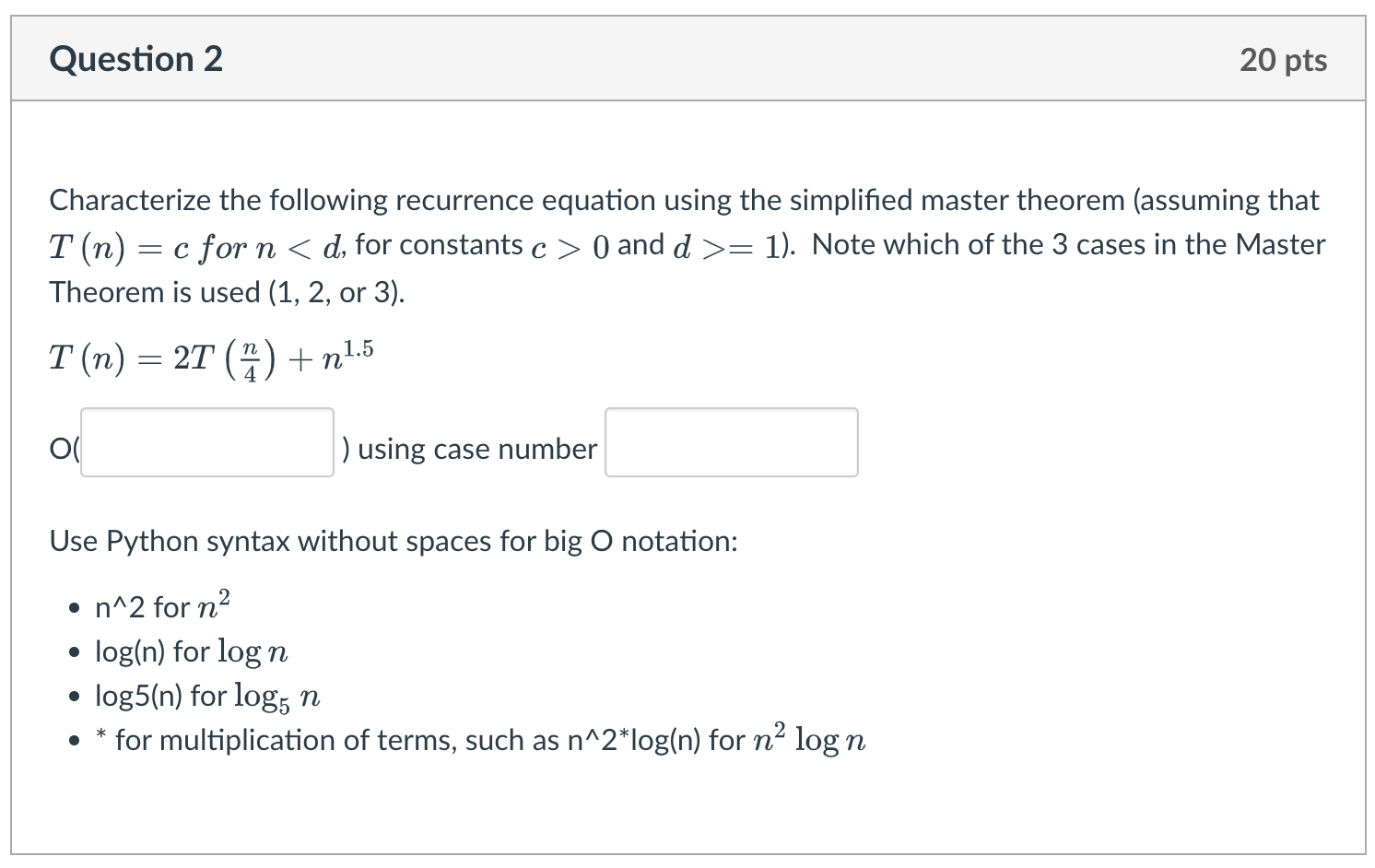
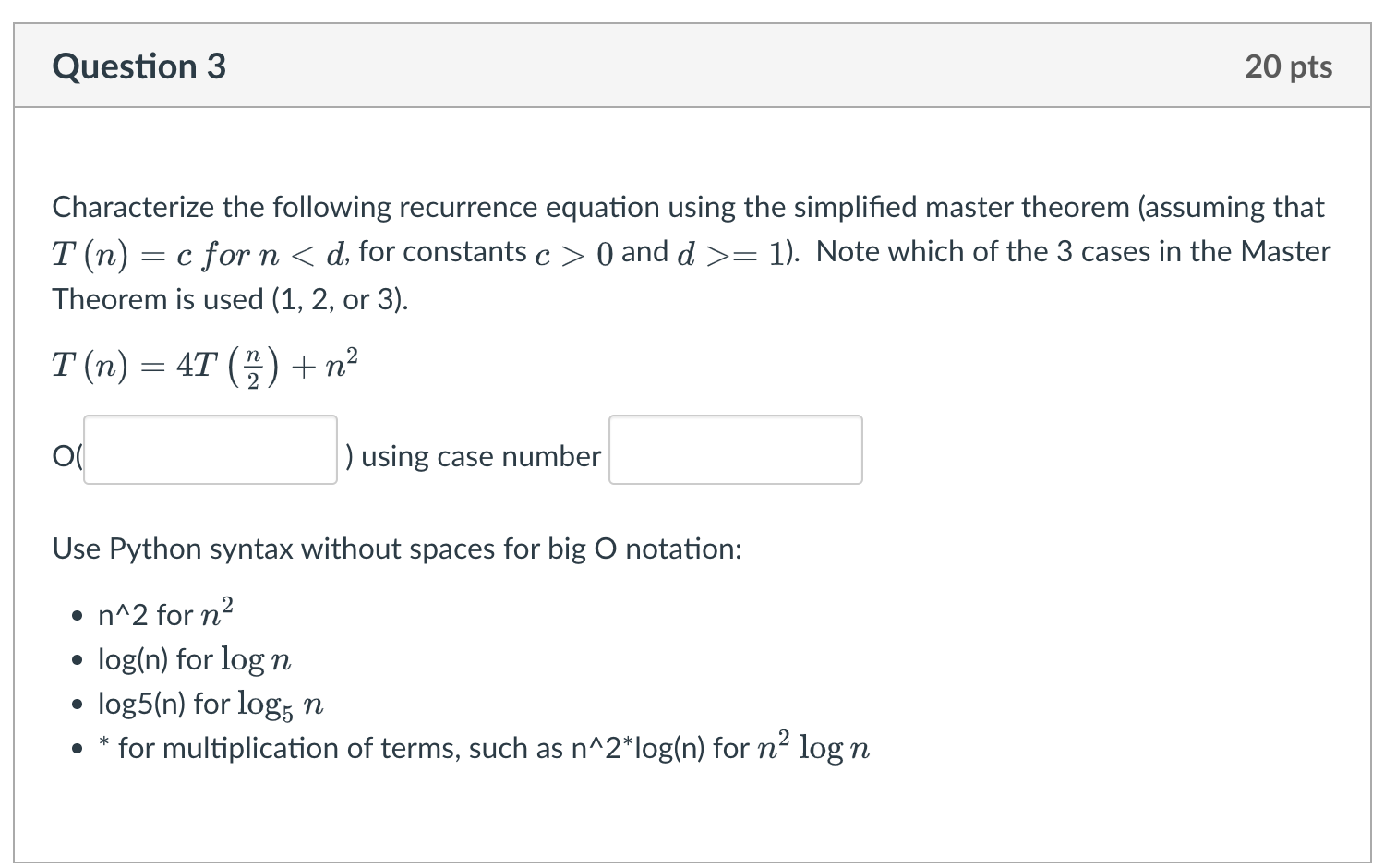
Select the big-Oh characterization, in terms of n, for the following loop. s=0fori=1ton2doforj=1toidos=s+i O(n2) O(nlogn) O(n4) O(n3) O(2n) O(1) O(n) O(logn) O(4n) Characterize the following recurrence equation using the simplified master theorem (assuming that T(n)=c for n
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


