how long does it take ?!

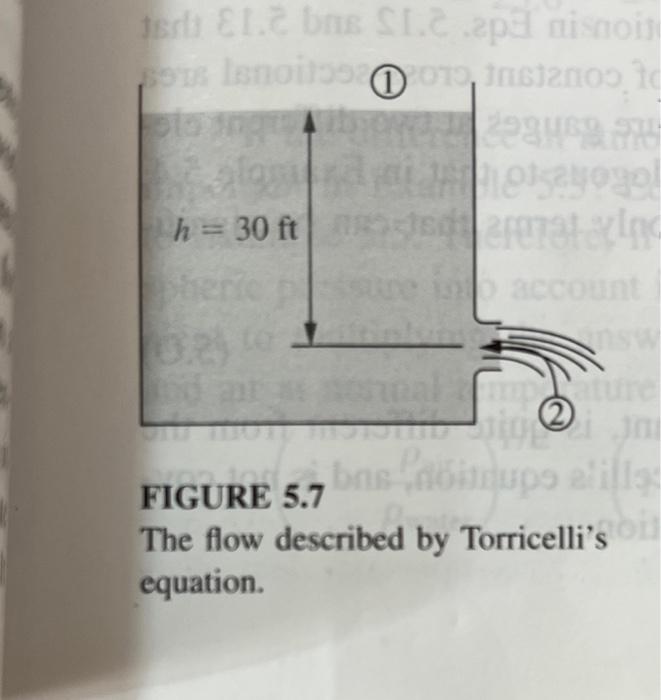
FIGURE 5.7 The flow described by Torricelli's equation. Example 5.14. If the tank in Fig. 5.7 is cylindrical with a diameter of 10m, and if the outlet nozzle is 1m in diameter, how long does it take the fluid level to drop from 30m above the tank outlet to 1m above the tank outlet? Here we assume that the (V/t)x,y,z is small; we will check that assumption later. The instantaneous flow rate is assumed to be given by B.E., which here takes the form of Torricelli's equation: V2=(2gh)1/2 But, by the mass balance for an incompressible fluid, V2=V1A2A1 where V1 is the rate at which the free surface of the tank is moving downward, which is equal to dh/dt; so V2=dtdhA2A1=(2gh)1/2:h1/2dh=A1A2(2g)1/2dth1h2h1/2dh=2h1/2]h1h2=A1A2(2g)1/2t1t2dt=A1A2(2g)1/2t]t11/2 Therefore, t=t2t1=(A2/A1)(2g)1/22(h21/2h11/2)[frictionlesstankdraining] Inserting numbers, we find t=[(/4)(1m)2/(/4)(10m)2](29.81m/s2)1/22[(1m)1/2(30m)1/2]=2.02102s=3.37min FIGURE 5.19 The maximum velocity in this tank is at the outlet, and Opening the valve all other velocities are proportional to it; therefore, the maxiproduces a flow not mum value of (V/t)x,y,z must occur at the outlet. Differentidescribed by Bernoulli's ating Torricelli's equation with respect to time, we find equation. tV2=2h1/2dt(2g)1/2dh Substituting for dh/dt, we find tV2=(2hg)1/2V2A1A2=(2hg)1/2(2gh)1/2A1A2=gA1A2 Thus, in this example the maximum value of (V/t)x,y,z is 1001 the acceleration of gravity, and the unsteady-flow aspect of the problem can safely be neglected