How might I address practice 5.13 from Bayesian information Analysis from Andrew Gelman utilizing stan and 'noninformative' hyperprior utilizing stan? I don't know to the correct method to make the stan model.

The 5.13 inquiry is (remember that I need to tackle utilizing Stan and noninformative hyperpriors - the book is free and accessible at: https://users.aalto.fi/~ave/BDA3.pdf) :

"Exercise 3.8 portrayed a study of bike traffic in Berkeley, California, with information showed in Table 3.3. For this issue, confine your consideration regarding the initial two lines of the table: private roads marked as 'bicycle courses,' which we will use to outline this computational exercise.

(a) Set up a model for the information in Table3.3so that, for j= 1,...,10, the noticed number of bikes at area j is binomial with obscure likelihood ?j and test size equivalent to the complete number of vehicles (bikes remembered) around there. The boundary ?j can be deciphered as the hidden or 'genuine' extent of traffic at area j that is bikes. (See Exercise3.8.) Assign a beta populace dissemination for the boundaries ?j and a noninformative hyperprior circulation as in the rodent tumor illustration of Section 5.3. Record the joint back appropriation.

(b) Compute the minor back thickness of the hyperparameters and draw recreations from the joint back dispersion of the boundaries and hyperparameters, as in Section 5.3.

(c) Compare the back circulations of the boundaries ?j to the crude extents, (number of bikes/complete number of vehicles) in area j. How do the inductions from the back dispersion vary from the crude extents?

(d) Give a 95% back stretch for the normal hidden extent of traffic that is bikes.

(e) another city block is inspected aimlessly and is a private road with a bicycle course. In an hour of perception, 100 vehicles of different types pass by. Give a 95% back stretch for the quantity of those vehicles that are bikes. Examine the amount you confide in this span in application.

(f) Was the beta dissemination for the ?j's sensible?

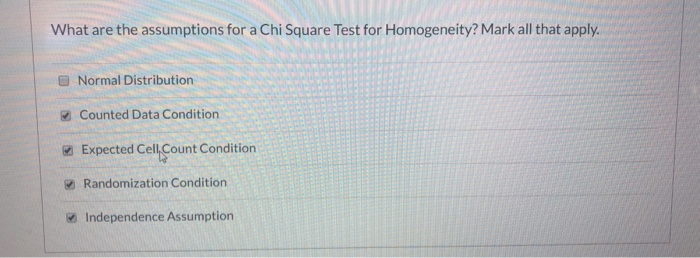
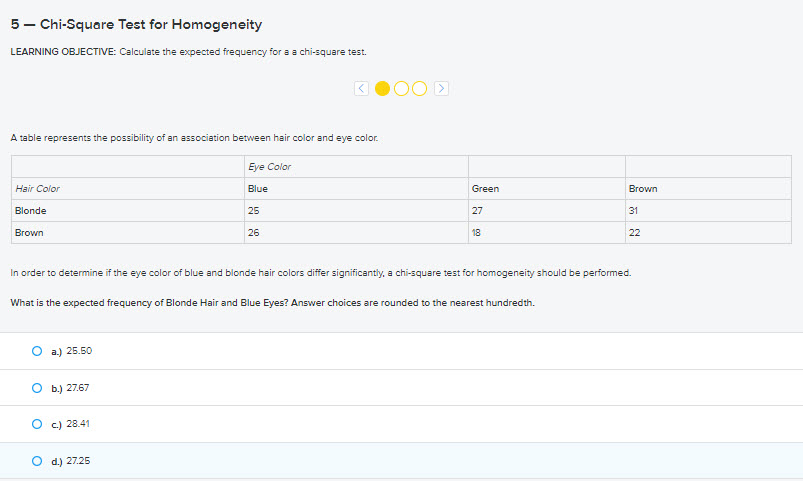
What are the assumptions for a Chi Square Test for Homogeneity? Mark all that apply. Normal Distribution Counted Data Condition Expected Cell Count Condition Randomization Condition Independence Assumption5 - Chi-Square Test for Homogeneity LEARNING OBJECTIVE: Calculate the expected frequency for a a chi-square test. K OOO D A table represents the possibility of an association between hair color and eye color. Eye Color Hair Color Blue Green Brown Blonde 26 27 31 Brown 26 18 22 In order to determine if the eye color of blue and blonde hair colors differ significantly, a chi-square test for homogeneity should be performed. What is the expected frequency of Blonde Hair and Blue Eyes? Answer choices are rounded to the nearest hundredth. a.) 25.50 O b.) 27.67 O c.) 28.41 O d.) 27.25A realtor wants to compare the mean sales-to-appraisal ratios of residential properties sold in four neighborhoods (A, B. C, and D). Four properties are randomly selected from each neighborhood and the ratios recorded for each, as shown below. A: 1.2, 1.1, 0.9, 0.4 C: 1.0, 1.5, 1.1, 1.3 B: 2.5, 2.1, 1.9, 1.6 D: 0.8, 1.3, 1.1, 0.7 Interpret the results of the analysis summarized in the following table: Source df SS MS F PR > F Neighborhoods 3.1819 1.0606 10.76 0.001 Error 12 Total 4.3644 1. Which of the following is correct? a. at the 0.05 level of significance, the mean ratios for the 4 neighborhoods are not all the same. b. at the 0.01 level of significance, the mean ratios for the 4 neighborhoods are all the same. c. at the 0.10 level of significance, the mean ratios for the 4 neighborhoods are not significantly different. d. at the 0.05 level of significance, the mean ratios for the 4 neighborhoods are not significantly different from 0. 2. What are the among group degrees of freedom, within group sum of squares and within group mean squares? 3. Please define the hypothesis for Levene's test for homogeneity of variances 4. Calculate the value of the test statistic for Levene's test for homogeneity of variances 5. Find the critical value of Levene's test for homogeneity of variances at a 5% level of significance is 6. What should be the decision for the Levene's test for homogeneity of variances at a 5% level of significance? 7. What is the conclusion for the Levene's test for homogeneity of variances at a 5% level of significance