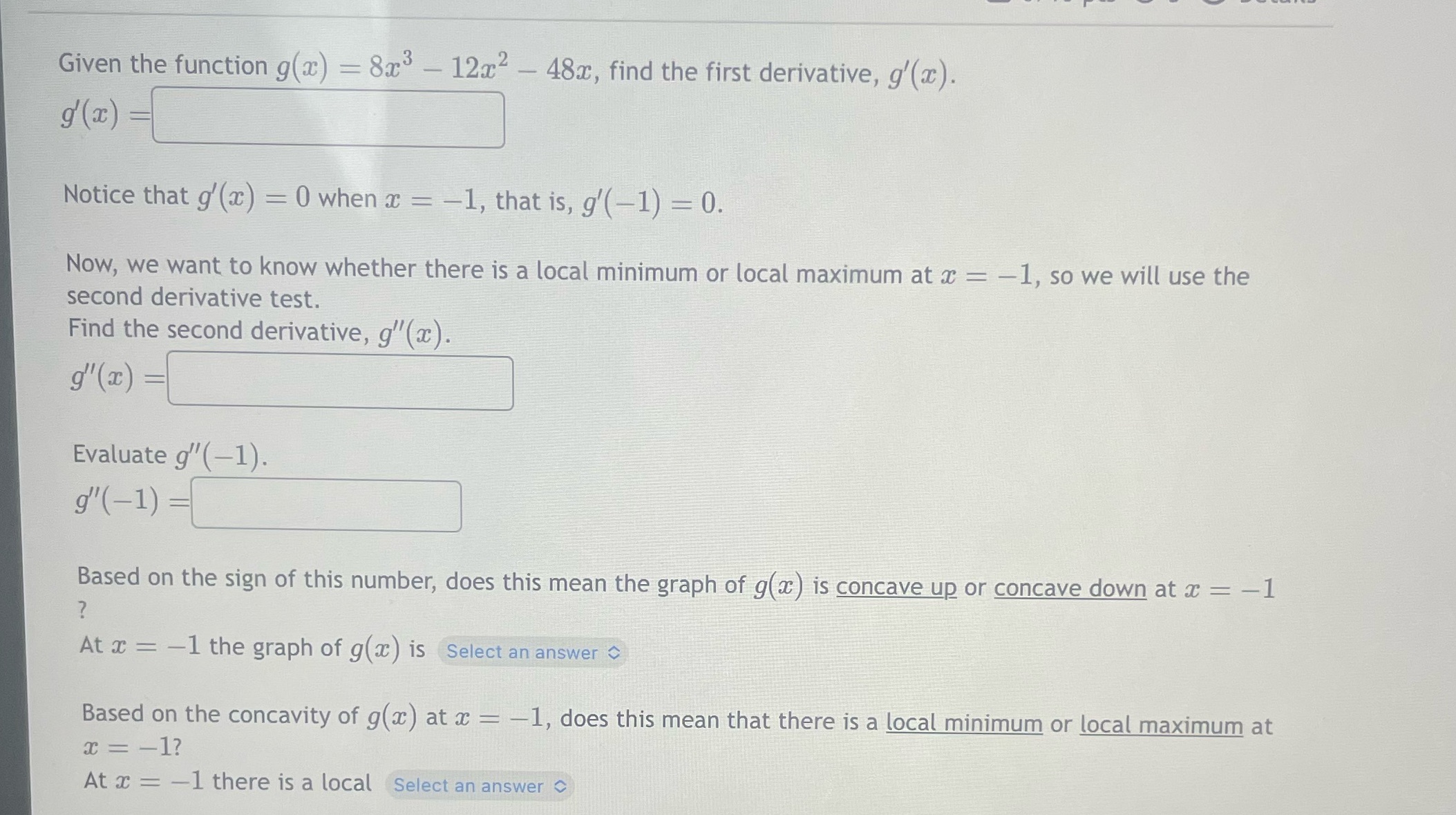
How to solve?

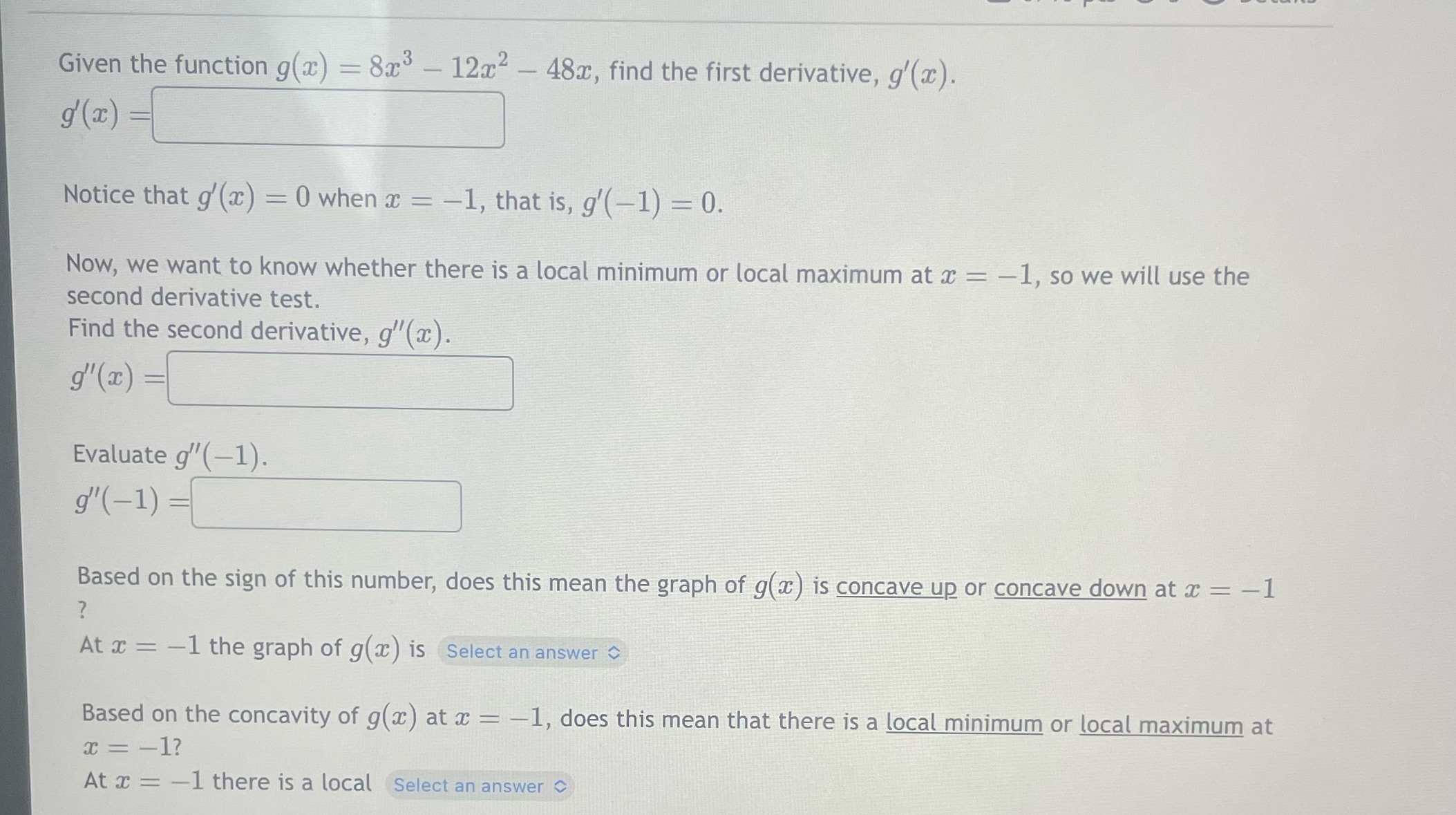
Given the function g(x) = 8x3 - 12x2 - 48x, find the first derivative, g'(x). g (x) Notice that g'(x) = 0 when x = -1, that is, g'( -1) = 0. Now, we want to know whether there is a local minimum or local maximum at a = -1, so we will use the second derivative test. Find the second derivative, g"(x). g" (x) Evaluate g"(-1). g ( - 1 ) Based on the sign of this number, does this mean the graph of g(a) is concave up or concave down at x = -1 ? At x = -1 the graph of g(x) is Select an answer Based on the concavity of g(x ) at x - -1, does this mean that there is a local minimum or local maximum at a = -1? At x = -1 there is a local Select an answer C