Question: how to: write a number in a base other than ten Add two or three numbers in a base other than ten Subtract two numbers

how to:
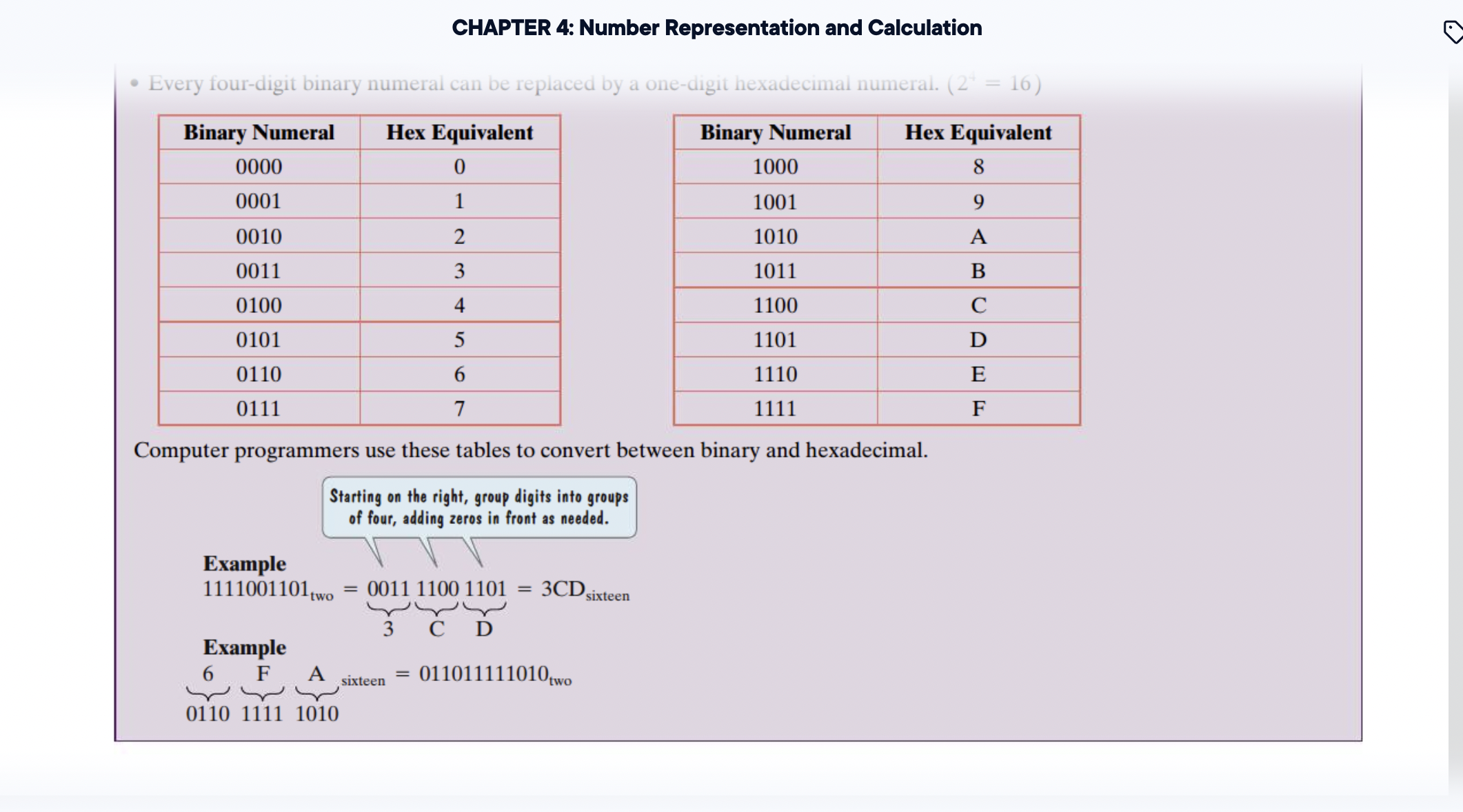
- write a number in a base other than ten
- Add two or three numbers in a base other than ten
- Subtract two numbers in a base other than ten
- Why do we learn to work with numbers in different bases?
Please provide detailed explanation and numerical examples for each answer.

WHAT AM I SUPPOSED TO LEARN? After studying this section, you should be able to: 1 Change numerals in bases other than ten to base ten. 2 Change base ten numerals t0 numerals in other bases. CHAPTER 4: Number Representation and Calculation Number Bases in Positional Systems YOU ARE BEING DRAWN DEEPER into cyberspace, spending more time online each week. With constantly improving high-resolution images, cyberspace is reshaping your life by nourishing shared enthusiasms. The people who built your computer talk of bandwidth that will give _ J .3 .. ' you the visual experience, in ' 2 .. . .35 o' high-definition 3-D format, of J a: e ' being in the same room with a person who is actually in another city. Because of our ten ngers and ten toes, the base ten Hindu-Arabic system seems to be an obvious choice. However, it is not base ten that computers use to process information and communicate with one another. Your experiences in cyberspace are sustained with a binary, or base two, system. In this section, we study numeration systems with bases other than ten. An understanding of such systems will help you to appreciate the nature of a positional system. You will also attain a better understanding of the computations you have used all of your life. You will even met tn (PP how the \\x'nrl lnnL'C frnni ('rnmltofc nint of view Change numerals in bases other than ten to base ten. TABLE 4.3 CHAPTER 4: Number Representation and Calculation Changing Numerals in Bases Other Than Ten to Base Ten The base of a positional numeration system refers to the number of individual digit symbols that can be used in that system as well as to the number whose powers define the place values. For example, the digit symbols in a base two system are 0 and 1. The place values in a base two system are powers of 2: ....24,23,22,21, 1 or...,2 X2X2X2,2 X 2X2,2>

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

Write this by C# Create a console application which does the following: 1. Ask the user to enter six numbers, two digits each. 2. Save each number into six separate double variables. 3. Add the first...

1. Please explain to the class Tovy o Rewrite a number in a base other than ten o Add two or three numbers in a base other than ten o Subtract two numbers in a base other than ten o Why do we learn...

Write a script that enables the user to enter mathematical word problems like "Add two and three" and "Divide nine by three", then use string processing to break apart the string into the numbers and...

Write a MIPS calculator for floating point numbers. First, write four procedures: addCalc: This procedure will add two floating point numbers (in Sf12 and Sf13) and return the result in SfO. subCalc:...

please complete the answer sheet using 2016 annual report Financial Statement Analysis Project ANSWER SHEET Name(s): No. Question 1. Who is responsible for the financial statements and maintaining...

At this time we have a task for you to do . You are to write several functions that do binary math on character strings of ' T ' s and ' F ' s . The functions you will fill in are: WRITE USING THE...

If someone could help me out on this I would appreciat it. I have been struggling with some of this and I need it as soon as possible. Thanks. At this time we have a task for you to do. You are to...

I have less idea working on it, can anyone teach me it? Thanks. At this time we have a task for you to do. You are to write several functions that do binary math on character strings of '1's and...

Must use Scheme language to solve the question. Thank you! 1. Write a function updown which takes a list of numbers as a parameter and returns the list with each number changed according to the...

In a study, on the effect of caffeine on myocardial blood flow, 10 subjects had their blood flow measured before and after consuming caffeine.21 For this setting the differences do not follow a...

Statement of activities for the year ended December 31, 2020. (Amounts to be deducted should be indicated with a minus sign. Round the intermediate and final answers to the nearest dollar amount.)...

An inventory loss from a market decline of $ 1 , 8 0 0 , 0 0 0 occurred in May 2 0 2 6 , after its March 3 1 , 2 0 2 6 quarterly report was issued. None of this loss was recovered by the end of the...

can you change this too If the standard deviation is 8 thousand miles, the number of miles that will be traveled by at least 90% of the trucks is enter your response here miles. (Round to the nearest...