How would I answer these questions?

1.

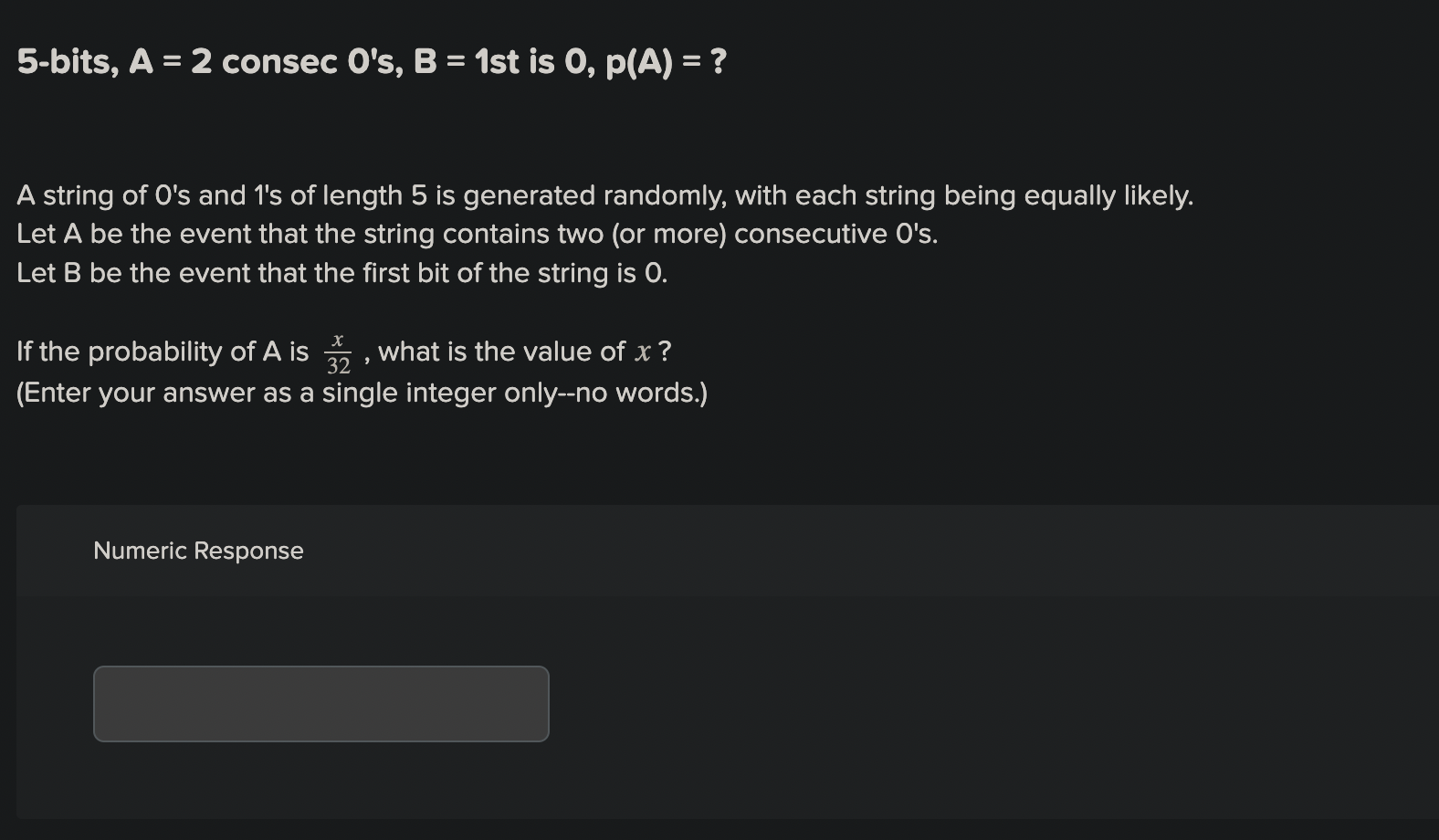
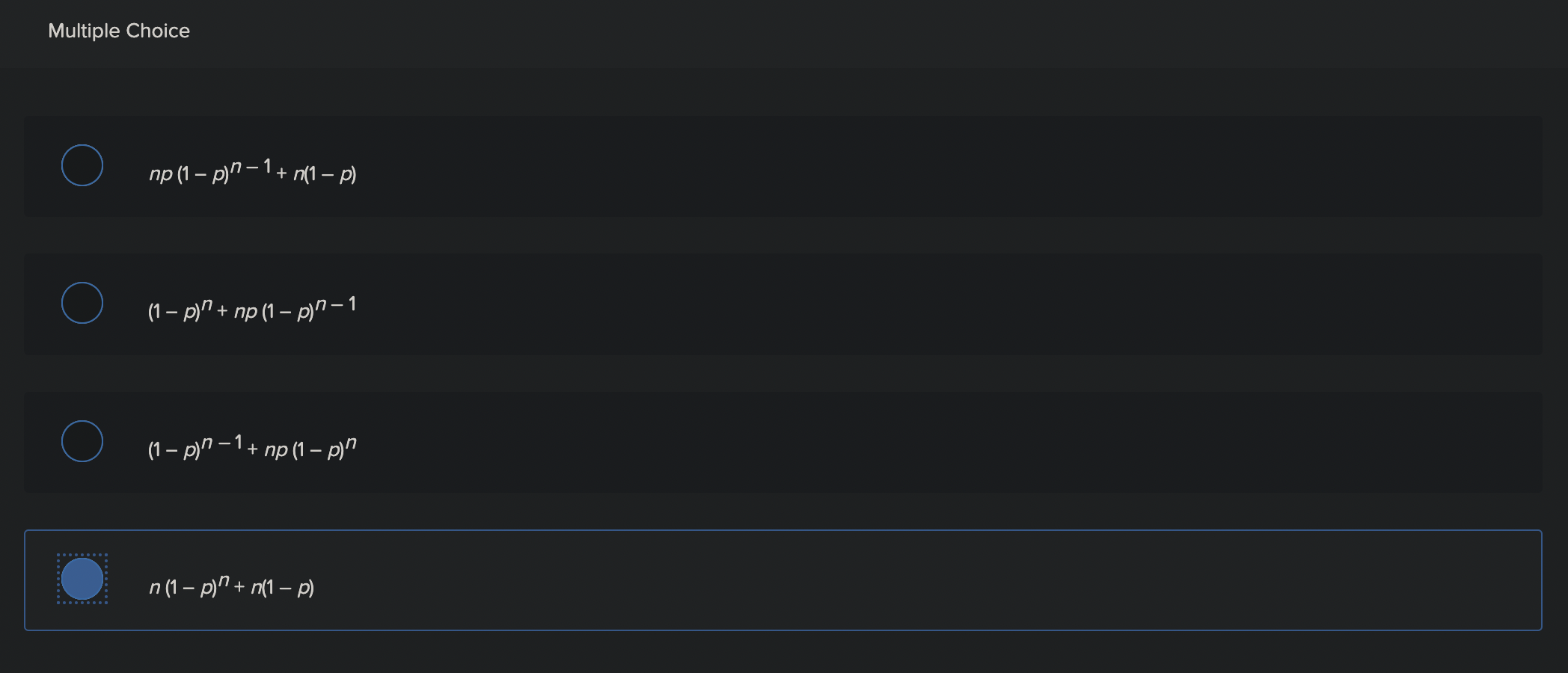
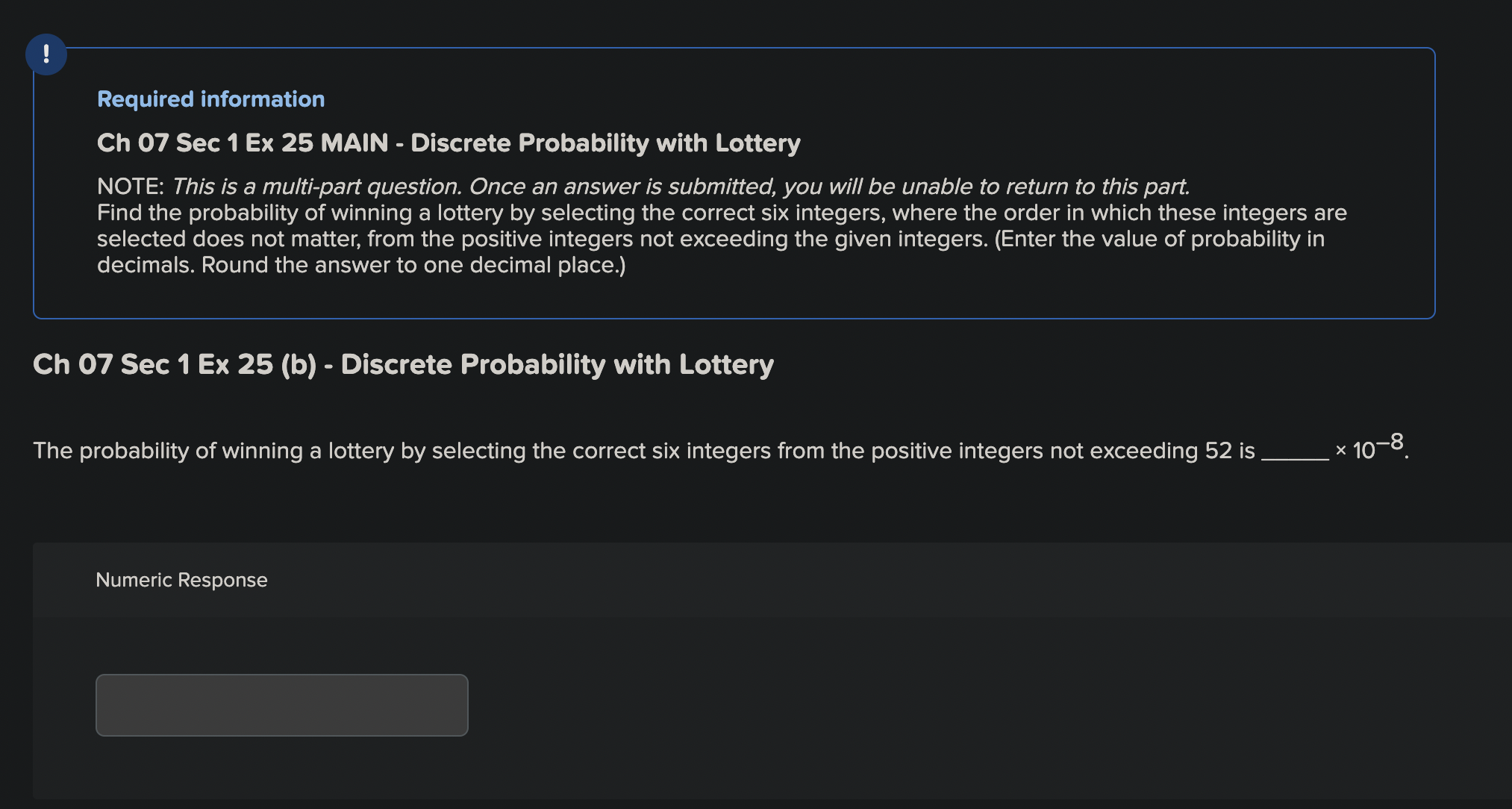
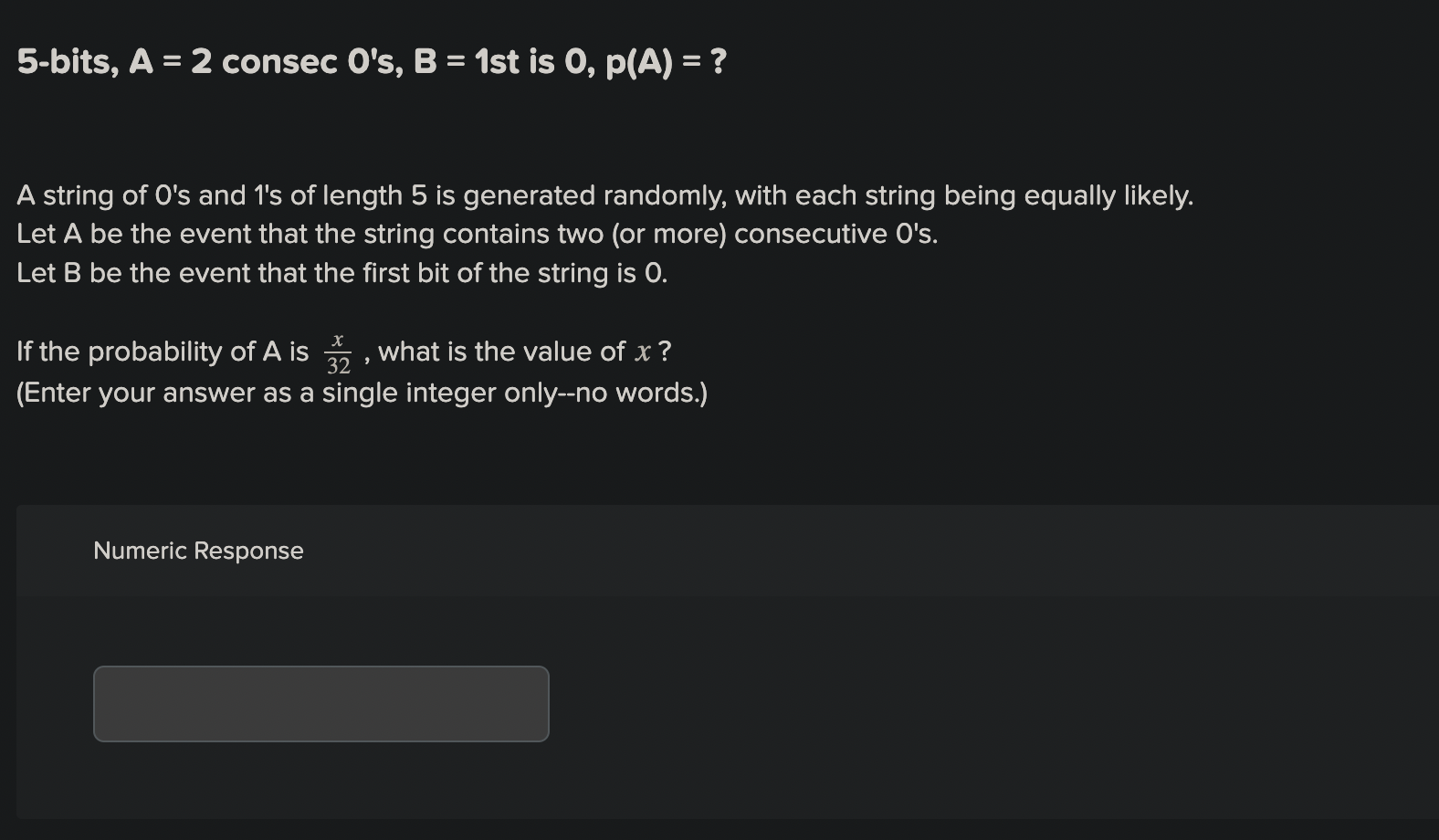
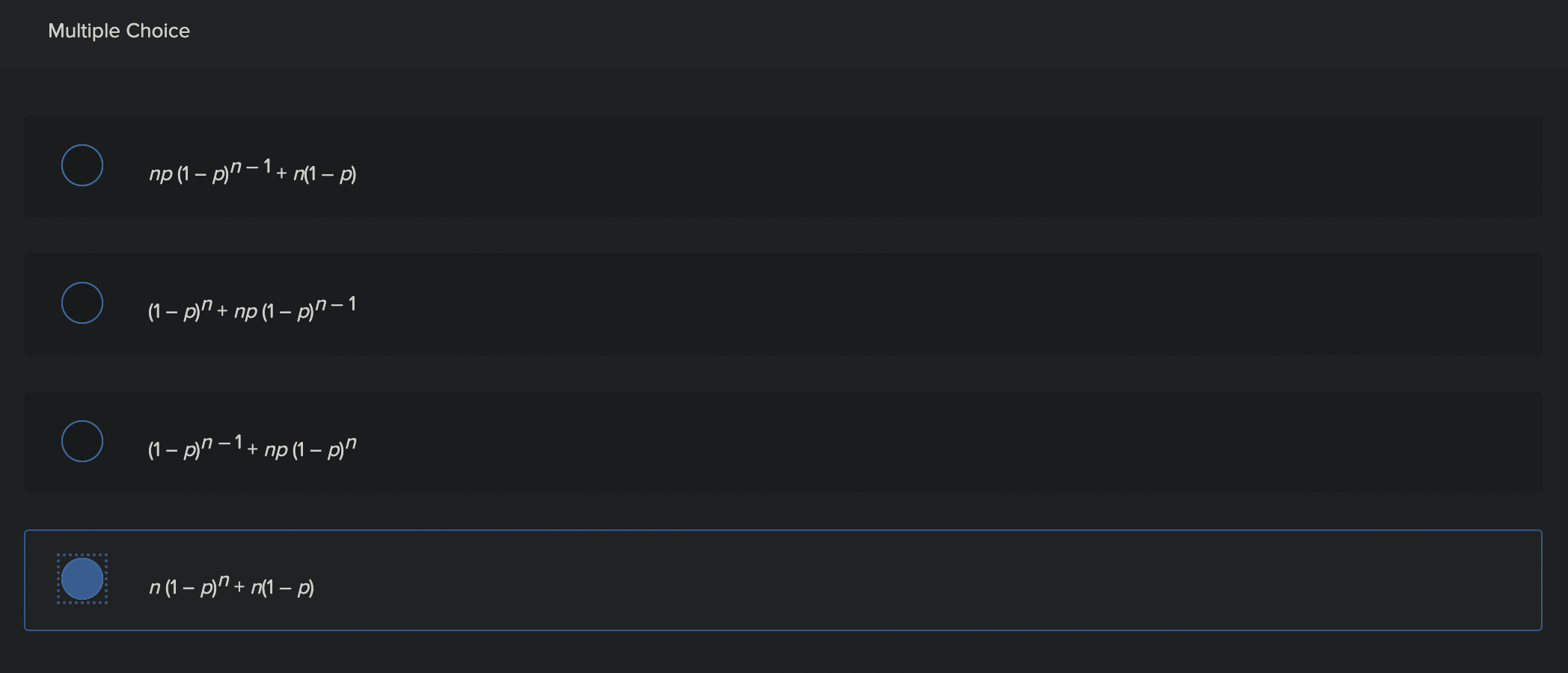
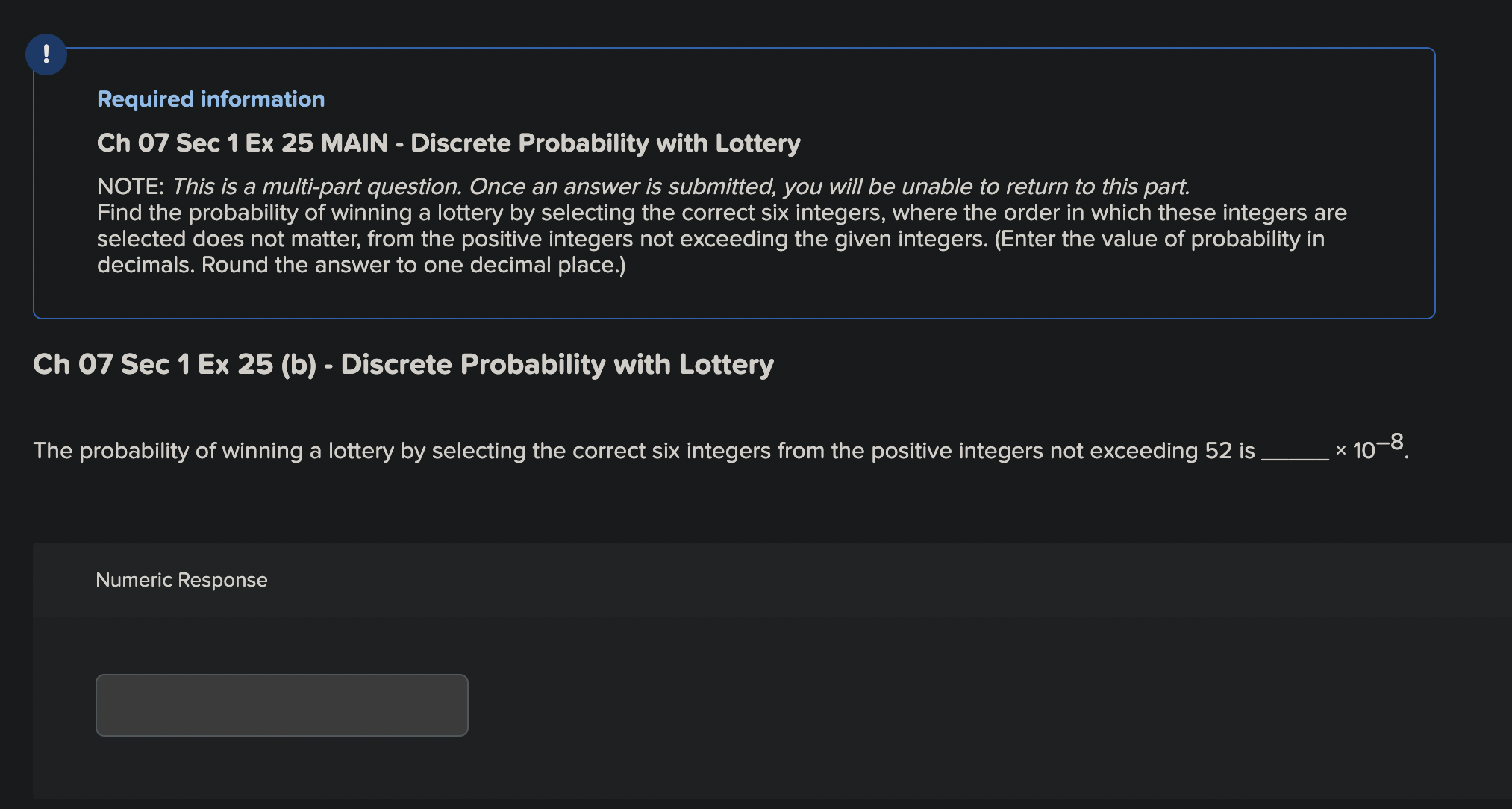
5-bits, A = 2 consec O's, B = 1st is 0, p(A) = ? A string of O's and 1's of length 5 is generated randomly, with each string being equally likely. Let A be the event that the string contains two (or more) consecutive O's. Let B be the event that the first bit of the string is 0. If the probability of A is 37 , what is the value of x ? (Enter your answer as a single integer only--no words.)5-bits, A = 2 consec O's, B = 1st is 0, p(A) = ? A string of O's and 1's of length 5 is generated randomly, with each string being equally likely. Let A be the event that the string contains two (or more) consecutive O's. Let B be the event that the first bit of the string is O. If the probability of A is 32 , what is the value of x? (Enter your answer as a single integer only--no words.) Numeric ResponseRequired information Ch 07 Sec 2 Ex 34 MAIN - Probabilty Theory using Bernoulli Trials - Theorem 2 NOTE: This is a multipart question Once an answer is submitted, you will be unable to return to this part. Find each of the following probabilities when n independent Bernoulli trials are carried out with probability of success p. Ch 07 Sec 2 Ex 34 (c) - Probabilty Theory using Bernoulli Trials - Theorem 2 the probability of at most one success \fRequired information Ch 07 Sec 1 Ex 25 MAIN - Discrete Probability with Lottery NOTE: This is a multipart question. Once an answer is submitted, you will be unable to return to this part. Find the probability of winning a lottery by selecting the correct six integers, where the order in which these integers are selected does not matter, from the positive integers not exceeding the given integers. (Enter the value of probability in decimals. Round the answerto one decimal place.) Ch 07 Sec 1 Ex 25 (b) - Discrete Probability with Lottery The probability of winning a lottery by selecting the correct six integers from the positive integers not exceeding 52 is X 108. Numeric Response