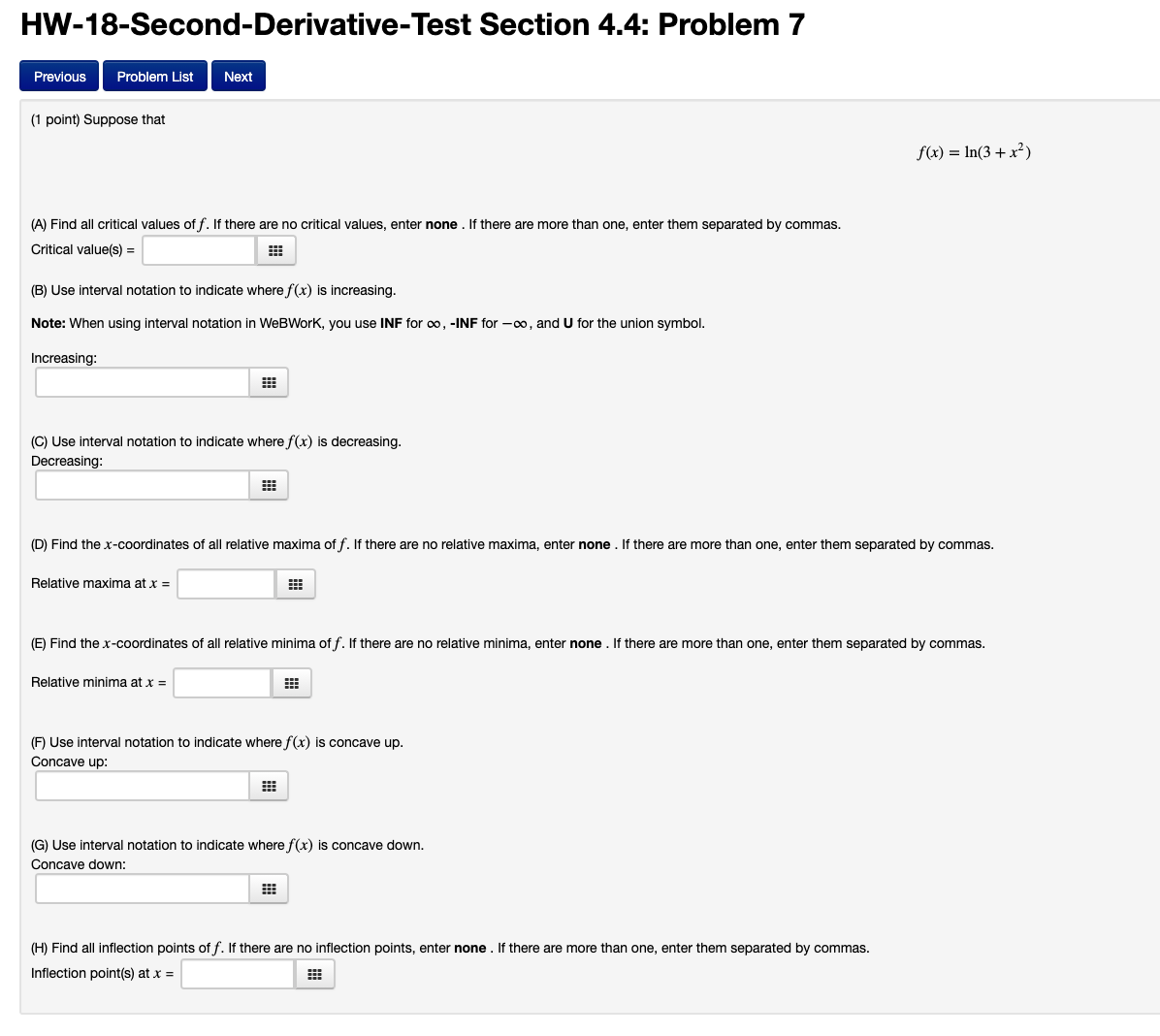
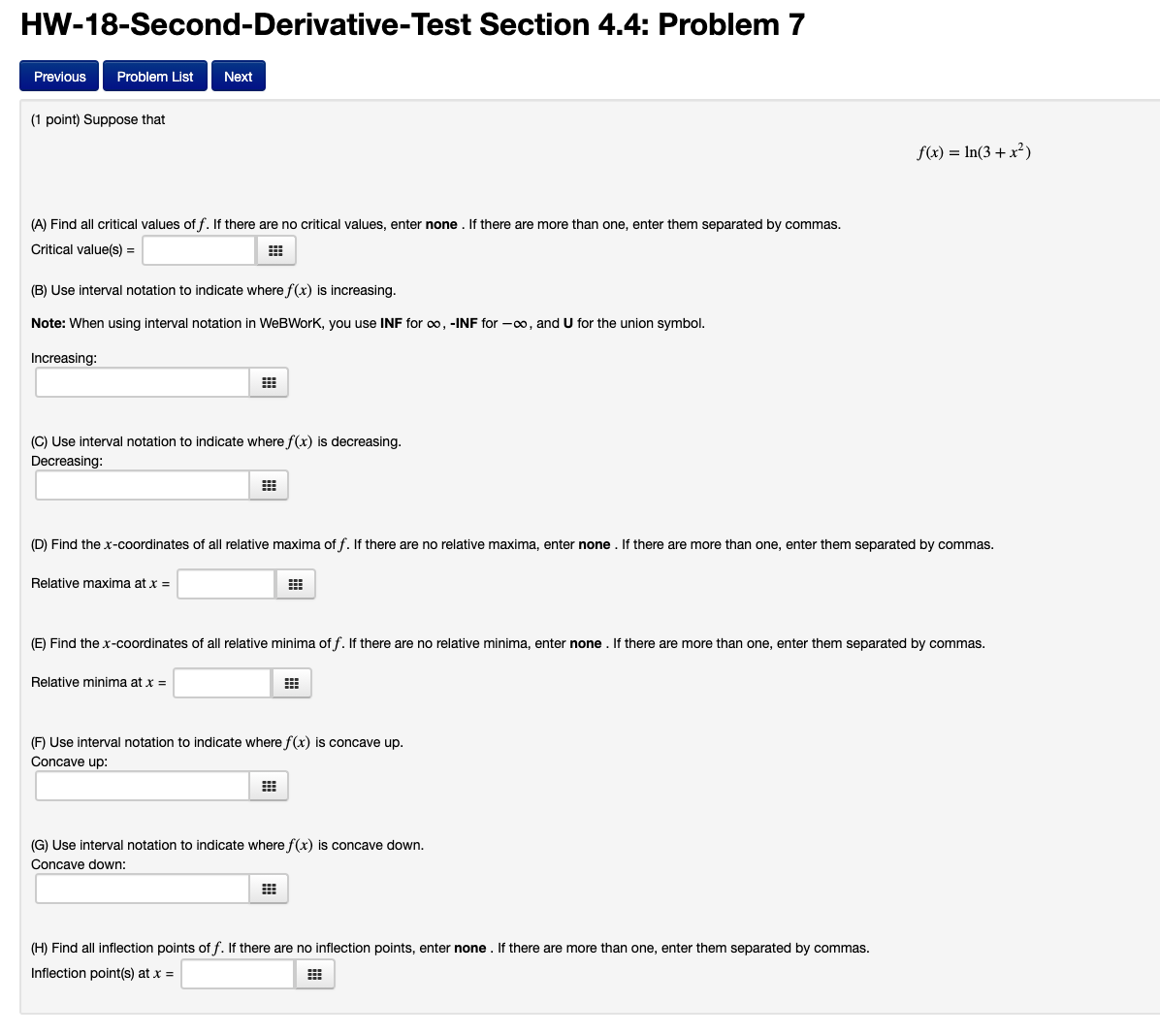
HW-18-Second-Derivative-Test Section 4.4: Problem 7 Previous Problem List Next (1 point) Suppose that f(x) = In(3 + x2) (A) Find all critical values of f. If there are no critical values, enter none . If there are more than one, enter them separated by commas. Critical value(s) = (B) Use interval notation to indicate where f(x) is increasing. Note: When using interval notation in WeBWork, you use INF for co, -INF for -co, and U for the union symbol. Increasing: C) Use interval notation to indicate where f(x) is decreasing. Decreasing (D) Find the x-coordinates of all relative maxima of f. If there are no relative maxima, enter none . If there are more than one, enter them separated by commas. Relative maxima at x = (E) Find the x-coordinates of all relative minima of f. If there are no relative minima, enter none . If there are more than one, enter them separated by commas. Relative minima at x = (F) Use interval notation to indicate where f(x) is concave up. Concave up: (G) Use interval notation to indicate where f (x) is concave down. Concave down: (H) Find all inflection points of f. If there are no inflection points, enter none . If there are more than one, enter them separated by commas. Inflection point(s) at x =