Question: HW-18-Second-Derivative-Test Section 4.4: Problem 6 Previous Problem List Next (1 point) Suppose that f(x ) =x4 -5x3. (A) Find all critical values of f. If

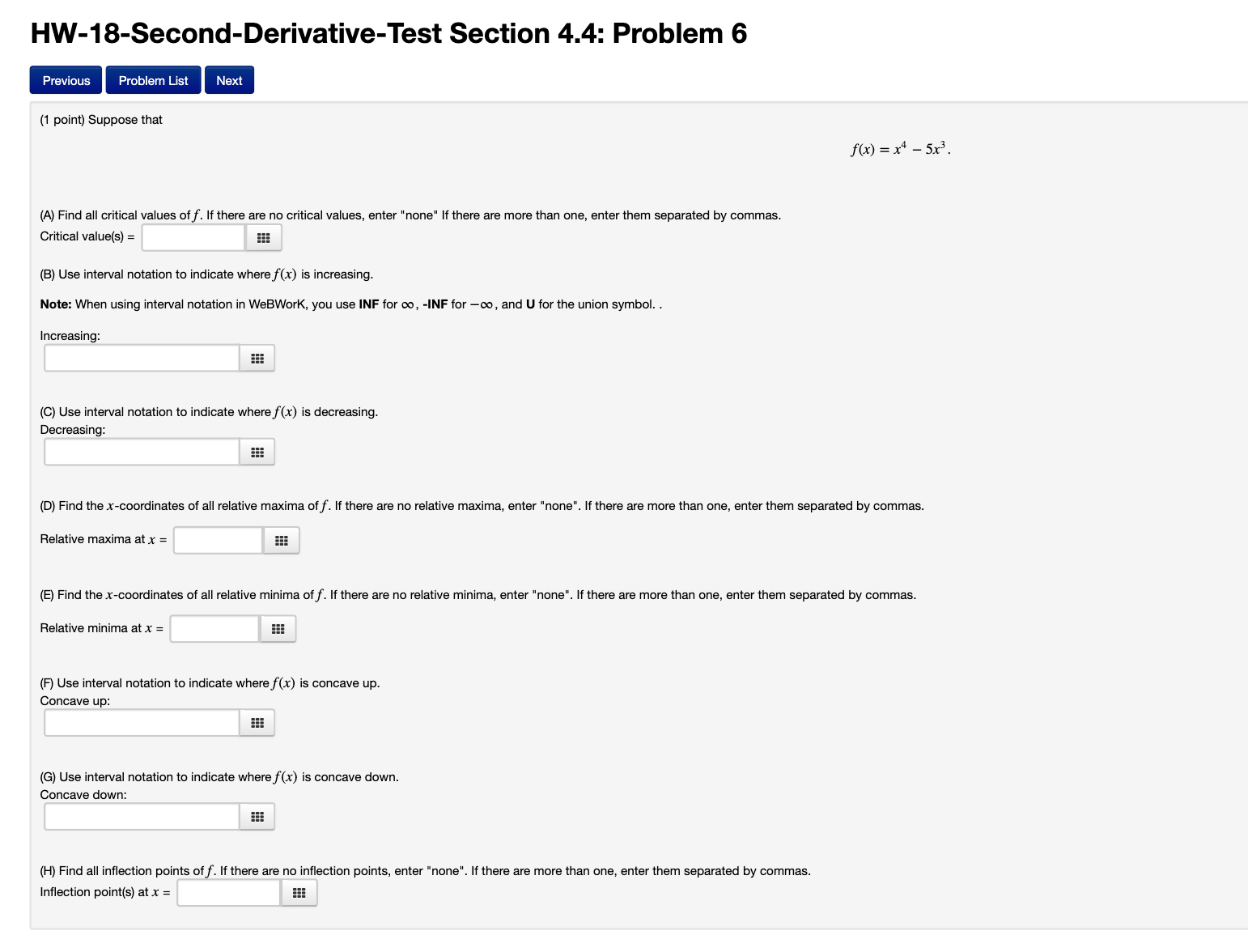
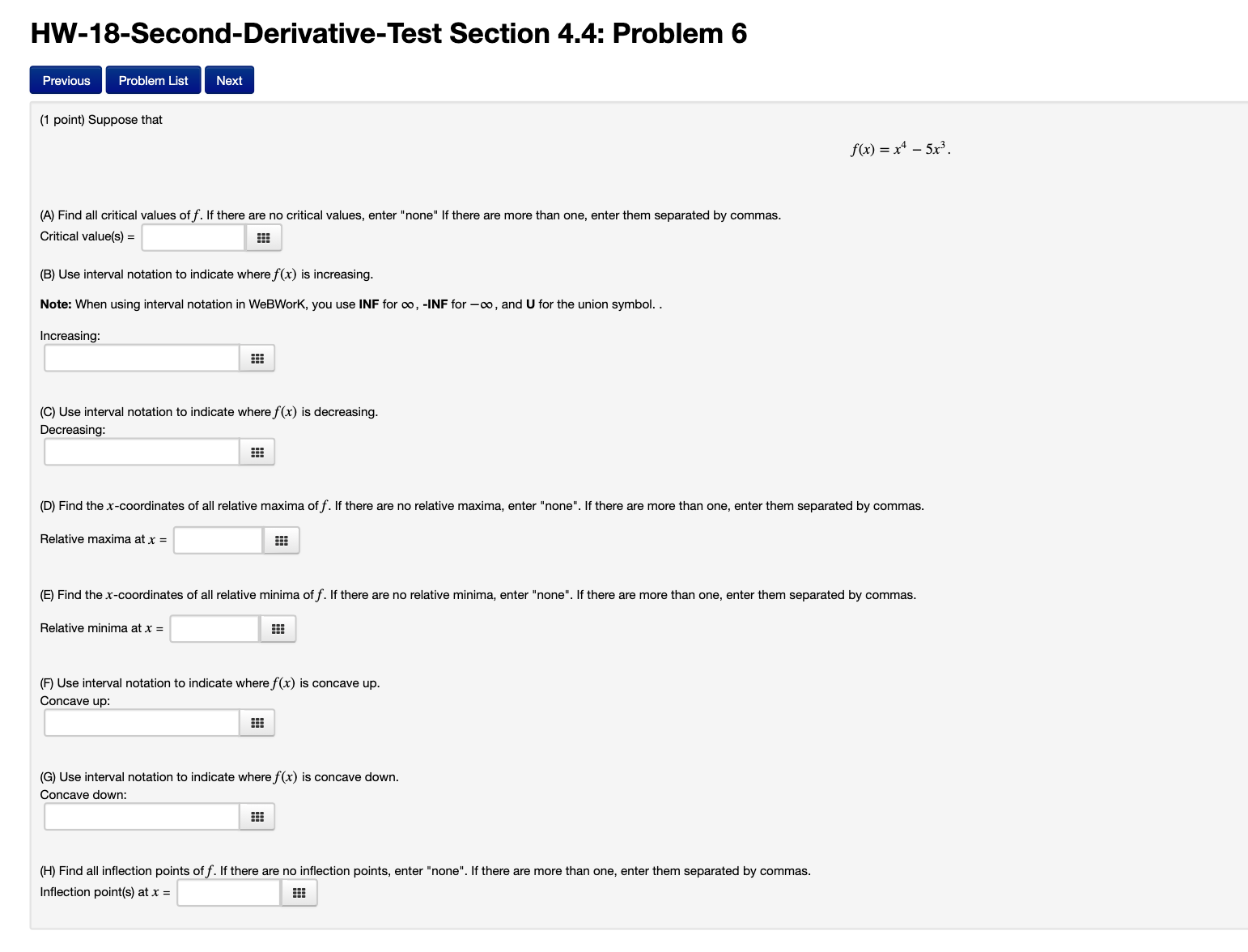
HW-18-Second-Derivative-Test Section 4.4: Problem 6 Previous Problem List Next (1 point) Suppose that f(x ) =x4 -5x3. (A) Find all critical values of f. If there are no critical values, enter "none" If there are more than one, enter them separated by commas. Critical value(s) = (B) Use interval notation to indicate where f(x) is increasing. Note: When using interval notation in WeBWork, you use INF for co, -INF for -co, and U for the union symbol. . Increasing: (C) Use interval notation to indicate where f(x) is decreasing. Decreasing: (D) Find the x-coordinates of all relative maxima of f. If there are no relative maxima, enter "none". If there are more than one, enter them separated by commas. Relative maxim (E) Find the x-coordinates of all relative minima of f. If there are no relative minima, enter "none". If there are more than one, enter them separated by commas. Relative minima at X = (F) Use interval notation to indicate where f(x) is concave up. Concave up (G) Use interval notation to indicate where f(x) is concave down. Concave down: (H) Find all inflection points of f. If there are no inflection points, enter "none". If there are more than one, enter them separated by commas. Inflection point(s) at x =

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

HW-18-Second-Derivative-Test Section 4.4: Problem 7 Previous Problem List Next (1 point) Suppose that f(x) = In(3 + x2) (A) Find all critical values of f. If there are no critical values, enter none...

HW-18-Second-Derivative-Test Section 4.4: Problem 8 Previous Problem List Next (1 point) Suppose that f(x) = 7xe-0.2x (A) Find all critical values of f. If there are no critical values, enter "none"...

Week 3b - Section 2 1 Definition of the Derivative: Problem Previous Problem List Next (1 point) Suppose that f is given for x in the interval [0, 12] by x = 0 2 4 6 8 10 12 f(x) = -10-14 -18...

Section 6.3: Problem 6 Previous Problem Problem List Next Problem (1 point) Evaluate the integral. 4x + 14 x2 + 4x + 8 dx 2In((2x+2)^2+4)+3arctan((x+2)/2) +C Preview My Answers Submit AnswersSection...

Section 14.4: Problem 6 Previous Problem Problem List Next Problem Ow ow of (1 point) Assume that w = f ( 4ts2, 6s (x, y) = Tay, and of dy (x, y) = Find and 5 at Ow at asSection 14.4: Problem 7...

Hi, Can someone help me with these two problems? I cannot find the right answers. Thank you (H) Find all inflection points of f. If there are no inflection points, enter 1000. If there are more than...

Math 1152 Project #4 Solving Initial Value Problems using Power Series and the Laplace Transform Due: Tuesday, April 11 Name(s): - - - - - - - - - - - - - - - - - - - - Description - - - - - - - - -...

Calculus 3 (Math-UA-123) Fall 2016 Homework 6 Due: Thursday, October 27 at the start of class Please give complete, well-written solutions to the following exercises. 1. Consider the function f (x,...

Activity 4 Full Assignment General Instructions: Please place your name above, then complete the following questions. NOTE: Read the entire document below to geta feel for the activity before...

Math\t107-6381\t-\tQuiz\t#4\t-\tSchultz\t-\tDue\tFebruary\t21,\t2016\t-\tpage\t1\tof 3 Follow\tthese\tdirections\tcarefully. This\tquiz\tis\tdue\tby\t11:59\tEastern\ttime\ton\tFebruary\t21,\t2016. o...

Many companies have potential pollution or environmental-disposal problems-not only for electronic gadgets, but also for the lead paint or asbestos they sold. How do we fit these issues into the...

"Swix is considering launching a mid-range athletic wear collection to target Millennials and Gen Z consumers, but they have many questions as to the expected quality of the merchandise, in which...

Case Study - Business Process Improvement A government department undertook a national programme to refresh technology and services across all its offices. Its programme finance team relied on...

Apply the VRIO framework to explain if the actions described in the statements below be a source of 1) competitive disadvantage, 2) parity of performance, 3) temporary advantage or 4) a sustained...

3. Imagine a communication situation at work or at home where you felt that you were locked (inflexible). Reflect on three alternative strategies that could have led to you becoming more flexible,...

4. In the next communication situation you are in, already think through three different communication strategies, which will make you achieve greater flexibility. Then practice on these as soon as...

2. Now imagine a real situation in your workplace or home situation where someone gives you feedback. a. Did you perceive the feedback as a hidden criticism? b. Did you perceive the feedback as a...