Question: Hyperbolic Functions Certain combinations of the exponential functions e x and e x arise so frequently in mathematics and its applications that they deserve

Hyperbolic Functions

Certain combinations of the exponential functions e^x and e^−x arise so frequently in mathematics and its applications that they deserve to be given special names. This project explores the properties of functions called hyperbolic functions. The hyperbolic sine hyperbolic cosine, hyperbolic tangent, and hyperbolic secant functions are defined as follows:

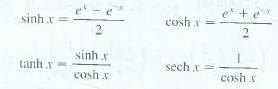
sinh x= tinh rem 2 e sinh r cosh x cosh x

The reason for the names of these functions is that they are related to the hyperbola in much the same way that the trigonometric functions are related to the circle.

The differentiation formulas for the hyperbolic functions are analogous to those for the trigonometric functions, but the signs are sometimes different.

(a) Show that (b) Discover formulas for the derivatives of y = cosh x and y = tanh x.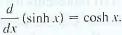 = sech x = et ti +e 2 cosh x

sinh x= tinh rem 2 e sinh r cosh x cosh x = sech x = et ti +e 2 cosh x

Step by Step Solution

★★★★★

3.43 Rating (159 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

To prove cosh xsinh x1 Consider left hand s... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Accounting Questions!

The complex hyperbolic functions are defined as (a) Write out the formulas for their real and imaginary parts in terms of z = x + iy. (b) Prove that cos i z = cos I z and sin i z = i sinhz. e e-2 ,...

The sine functions are defined as while Sj(x) = S0(x - j h) whenever h > 0 and j is an integer. We will interpolate a function /(x) at the mesh points Xj = jh, j = 0,... ,«, by a linear...

The tangent line to a circle may be defined as the line that intersects the circle in a single point, called the point of tangency. See the figure. If the equation of the circle is and the equation...

Match each trigonometric function with its right triangle definition. (a) sine (b) Cosine (c) Tangent (d) Cosecant (e) Secant (f ) Cotangent 1. Hypotenuse / adjacent 2. Adjacent / opposite 3....

2. (a) Use the Taylor series representation of complex exponentials e = E with z = ix (with x a real number and / = v-1) to derive Euler's formula out = cos(x) + isin(x). Hint. P = -1. (b) Show using...

Strategy balanced scorecard. Meredith Corporation makes a special-purpose machine, D4H, used in the textile industry. Meredith has designed the D4H machine for 2009 to be distinct from its...

Knowledge of the rules of conduct, interpretations thereof, and related rulings on independence, integrity, and objectivity will help you respond to the following cases. Required: For each case,...

a. Calculate the possible price/quantity combinations within the relevant range of production and the permissible pricing range and determine the optimum level of sales that will maximize...

According to quantum mechanics, only one of the following combinations of the principal quantum number n and the orbital quantum number, is possible for the electron in a hydrogen atom. Which...

Refer to Exercise 12-25. Stanmore Corporation makes a special-purpose machine, D4H, used in the textile industry. Stanmore has designed the D4H machine for 2017 to be distinct from its competitors....

Comprehensive Piedmont Manufacturing produces metal products with the following standard quantity and cost information: Direct Material Aluminum 4 sheets @ $4 $16 Copper 3 sheets @ $8 24 Direct labor...

Here is an interesting game presented and discussed by psychologists, mathematicians, philosophers, and people in business, risk management, and gambling. You start with $1, and a die is rolled. You...

Poh has just started working at a new manufacturing plant and she is struggling to remain motivated at work. At her old workplace, she created insulin pumps for patients with diabetes and assembled...

Find the amount (in $) of interest on the loan. Principal Rate (%) Time Interest $50,000 73 9 months tA $ 4

7. Make a table of values and graph each function. a) g(x) =-3x+5 for the domain (-3, -2, -1, 0, 1, 2, 3} b) h(x) = for the domain {x | -10 x 10, x = R} Apply 8. Mike currently has $200 and saves $20...

An important factor in choosing the best communication channel is its media richness. What does this concept meant, why it is useful to manager and briefly state how technology has contributed in...

Myers Company uses a flexible budget for manufacturing overhead based on direct labor hours. Variable manufacturing overhead costs per direct labor hour are as follows: Fixed overhead costs per month...

Uniform electric field in Figure a uniform electric field is directed out of the page within a circular region of radius R = 3.00 cm. The magnitude of the electric field is given by E = (4.50 x 10-3...

Dr. Ivan I. Incisor and his wife Irene are married and file a joint return for 2012. Ivan's Social Security number is 477-34-4321 and he is 48 years old. Irene I. Incisor's Social Security number is...

John Fuji (age 37) moved from California to Washington in December 2011. He lives at 468 Cameo Street, Yakima, WA 98901. John's Social Security number is 571-78-5974 and he is single. His earnings...

Dr. George E. Beeper is a single taxpayer. He lives at 45 Mountain View Dr., Apt. 321, Spokane, WA 99210. Dr. Beeper's Social Security number is 775-88-9531. Dr. Beeper works for the Pine Medical...

A random sample of 25 sport utility vehicles (SUVs) of the same year and model revealed the following miles per gallon (mpg) values: Assume that the population for mpg for this model year is normally...

According to an investigative reporter (Jim Drinkard, Legislators Want to Ground Fact-Finding Trips, USA Today, January 19, 2006), members of Congress are coming under scrutiny for fact-finding...

A random sample of 64 bicycle-riding adults in Portland indicated that 24 always wore a helmet while riding. Use the sample information to develop a 95% confidence interval estimate for the true...