I already have the files mentioned in section 2 (preparation). Those will be provided at the end for clarification. Please help with sections 3 and 4.

Files

function HT = HTrotx(alpha)

% Computes the homogeneous transformation matrix for a rotation around x-axis by angle alpha.

HT = [1 0 0 0;

0 cos(alpha) -sin(alpha) 0;

0 sin(alpha) cos(alpha) 0;

0 0 0 1];

end

function T = DHF(param)

% Extract DH parameters

alpha = param(1);

a = param(2);

d = param(3);

theta = param(4);

% Calculate DH transformation matrix

T = HTrotx(alpha) * HTtranx(a) * HTtranz(d) * HTrotz(theta);

end

function HT = HTrotz(theta)

% Computes the homogeneous transformation matrix for a rotation around z-axis b angle theta.

HT = [cos(theta) -sin(theta) 0 0;

sin(theta) cos(theta) 0 0;

0 0 1 0;

0 0 0 1];

end

function HT = HTtranx(a)

% Computes the homogeneous transformation matrix for a translation along x-axis by distance a.

HT = [1 0 0 a;

0 1 0 0;

0 0 1 0;

0 0 0 1];

end

function HT = HTtranz(d)

% Computes the homogeneous transformation matrix for a translation along z-axis by distance d.

HT = [1 0 0 0;

0 1 0 0;

0 0 1 d;

0 0 0 1];

end

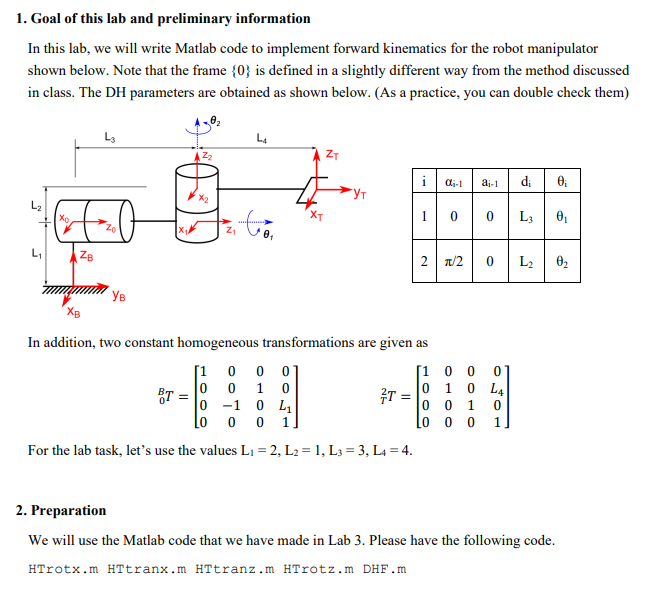
1. Goal of this lab and preliminary information In this lab, we will write Matlab code to implement forward kinematics for the robot manipulator shown below. Note that the frame {0} is defined in a slightly different way from the method discussed in class. The DH parameters are obtained as shown below. (As a practice, you can double check them) In addition, two constant homogeneous transformations are given as 0BT=10000010010000L11T2T=1000010000100L401 For the lab task, let's use the values L1=2,L2=1,L3=3,L4=4. 2. Preparation We will use the Matlab code that we have made in Lab 3. Please have the following code. HTrotx.m HTtranx.m HTtranz.m HTrotz.m DHF.m 3. Finding positions Write an m-file (test_lab4_1.m) that finds the following positions. (a) Find the positions of the origins of the frame {1},{2}, and {T} when 1=0 (rad) and 2=0 (rad) (b) Find the positions of the origins of the frame {1},{2}, and {T} when 1=4 (rad) and 2= 4(rad) Note: These positions should be defined using the base frame {B}. For example, the origin of {2} can be found in the homogeneous transformation matrix 2BT. This can be simply obtained using the equation 2BT=0BT10T21T 4. Drawing stick figures for a robot manipulator. Write an m-file entitled DrawRobot.m containing a function DrawRobot (th1, th2) that accepts two radian angles th1 and th2 and draw a stick figure of the robot that we are considering above. The stick figure consists of four lines as follows. Line 1 : between the origins of the frames {B} and {0} Line 2 : between the origins of the frames {0} and {1} Line 3 : between the origins of the frames {1} and {2} Line 4 : between the origins of the frames {2} and {T} Write an m-file (test_lab4_2.m) that draws stick figures using DrawRobot.m with the following angles. (a) Stick figure when 1=0(rad) and 2=0(rad) (b) Stick figure when 1=4(rad) and 2=4(rad) See the appendix to get familiar with Matlab built-in function plot3( )