I am learning about sparse matrices and the two level algorithm and PCG algorithm. Below are instructions on a project I am working on. I need help implementing this project in python. I want a step by step explanation and a running code. I am not turning this in I just need help because I don't have python experience. Notes and instructions to the project are provided in the screenshots. For the graph to use, use the one i provided in text format called karate club.

Here are some supporting documents:

the two-level algorithm:

PCG algorithm:

graph adjacency matrices in Coo format:

karate_club_graph-1-1.txt :

0 1 1
0 2 1
0 3 1
0 4 1
0 5 1
0 6 1
0 7 1
0 8 1
0 10 1
0 11 1
0 12 1
0 13 1
0 17 1
0 19 1
0 21 1
0 31 1
1 0 1
1 2 1
1 3 1
1 7 1
1 13 1
1 17 1
1 19 1
1 21 1
1 30 1
2 0 1
2 1 1
2 3 1
2 7 1
2 8 1
2 9 1
2 13 1
2 27 1
2 28 1
2 32 1
3 0 1
3 1 1
3 2 1
3 7 1
3 12 1
3 13 1
4 0 1
4 6 1
4 10 1
5 0 1
5 6 1
5 10 1
5 16 1
6 0 1
6 4 1
6 5 1
6 16 1
7 0 1
7 1 1

7 2 1
7 3 1
8 0 1
8 2 1
8 30 1
8 32 1
8 33 1
9 2 1
9 33 1
10 0 1
10 4 1
10 5 1
11 0 1
12 0 1
12 3 1
13 0 1
13 1 1
13 2 1
13 3 1
13 33 1
14 32 1
14 33 1
15 32 1
15 33 1
16 5 1
16 6 1
17 0 1
17 1 1
18 32 1
18 33 1
19 0 1
19 1 1
19 33 1
20 32 1
20 33 1
21 0 1
21 1 1
22 32 1
22 33 1
23 25 1
23 27 1
23 29 1
23 32 1
23 33 1
24 25 1
24 27 1
24 31 1
25 23 1
25 24 1
25 31 1
26 29 1
26 33 1
27 2 1
27 23 1

27 24 1
27 33 1
28 2 1
28 31 1
28 33 1
29 23 1
29 26 1
29 32 1
29 33 1
30 1 1
30 8 1
30 32 1
30 33 1
31 0 1
31 24 1
31 25 1
31 28 1
31 32 1
31 33 1
32 2 1
32 8 1
32 14 1
32 15 1
32 18 1
32 20 1
32 22 1
32 23 1
32 29 1
32 30 1
32 31 1
32 33 1
33 8 1
33 9 1
33 13 1
33 14 1
33 15 1
33 18 1
33 19 1
33 20 1
33 22 1
33 23 1
33 26 1
33 27 1
33 28 1
33 29 1
33 30 1
33 31 1
33 32 1

 

notes about NetworkX in python

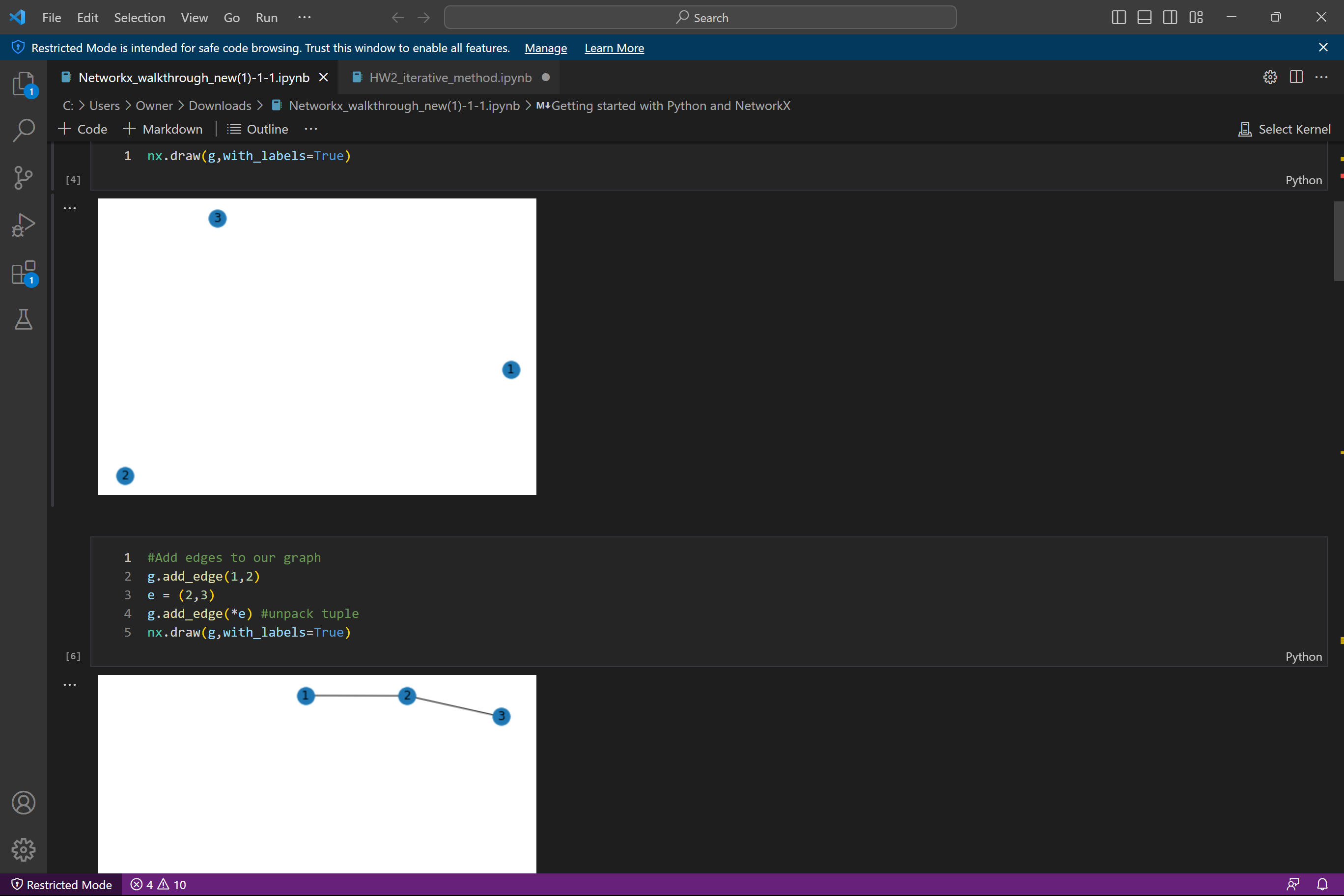
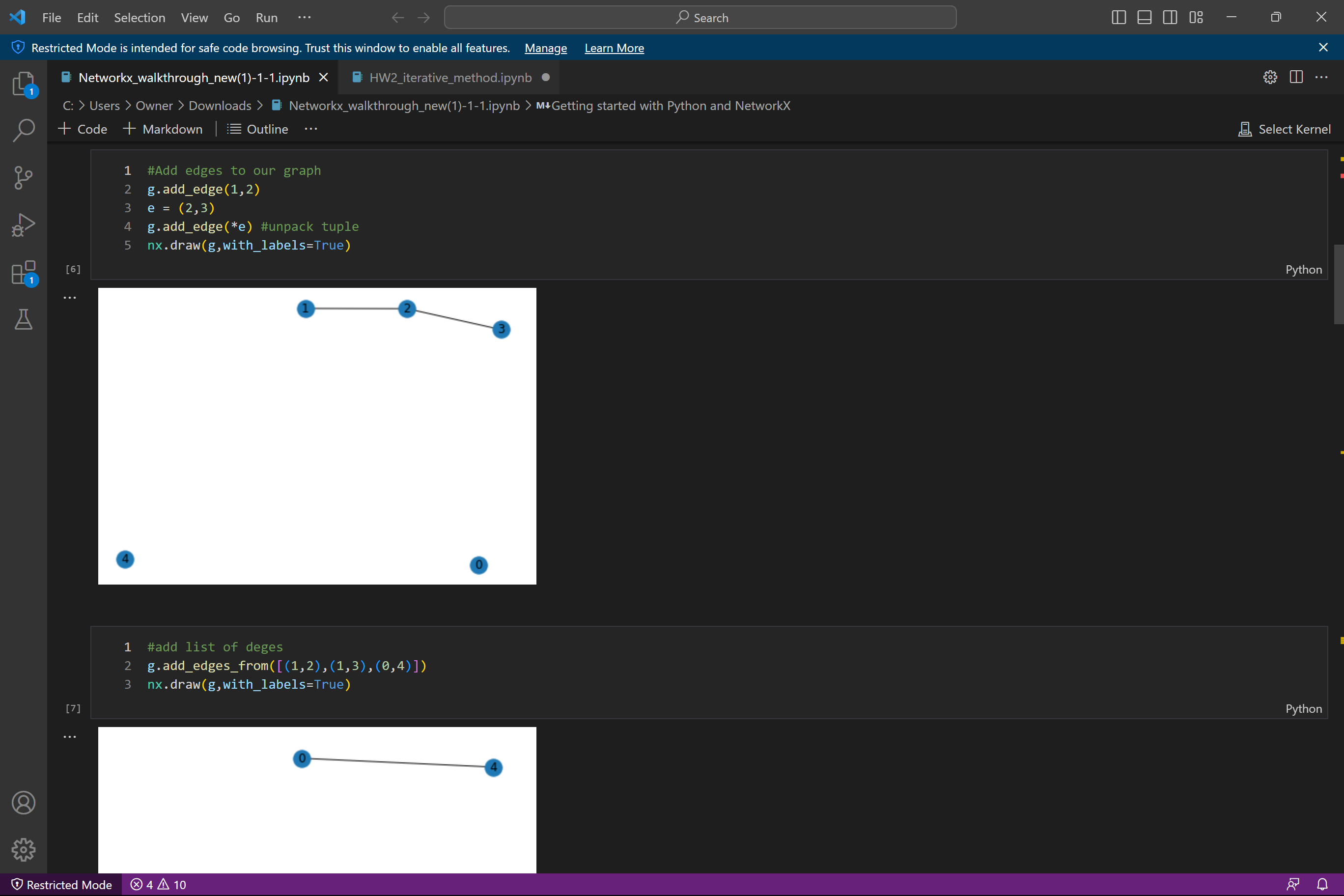
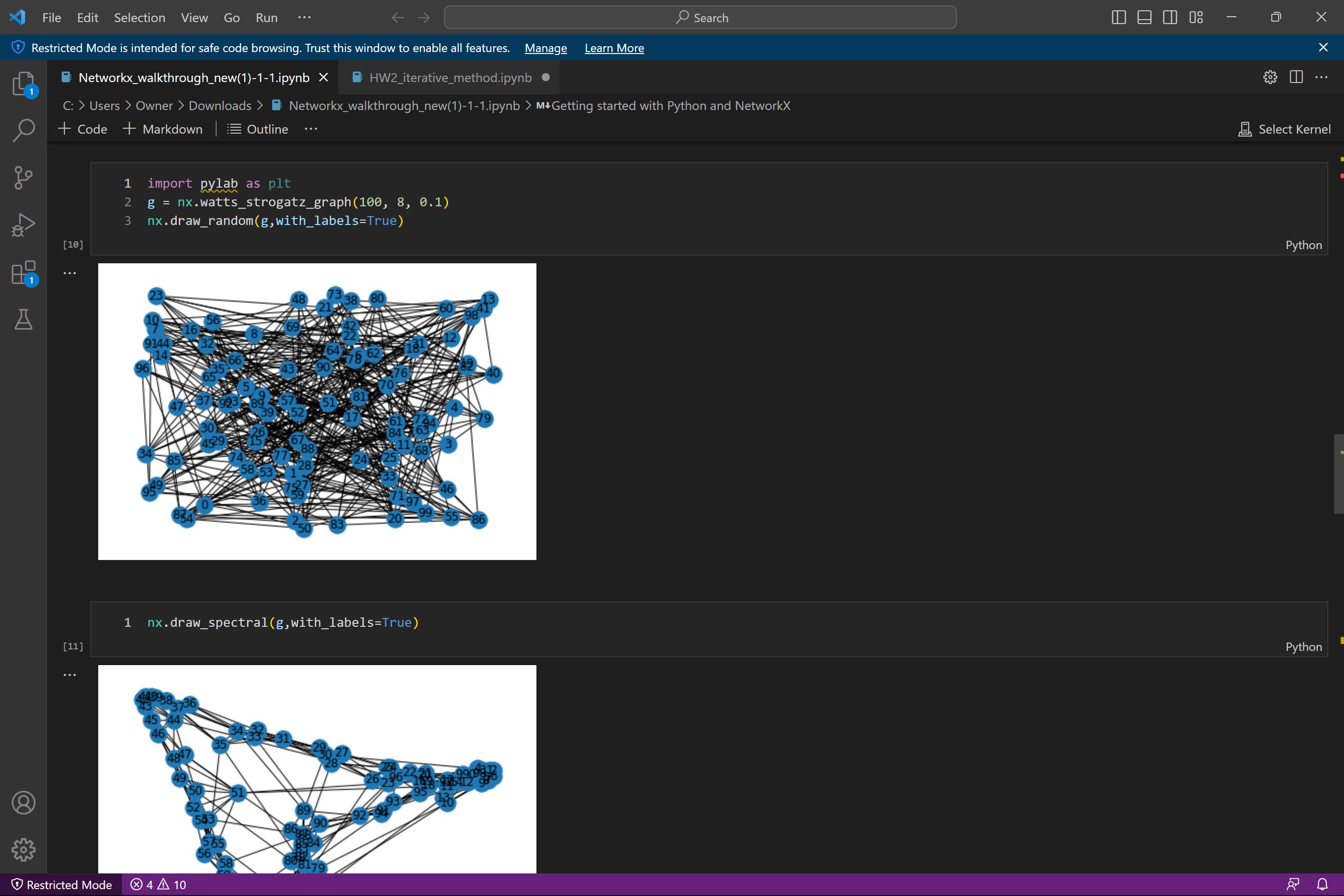
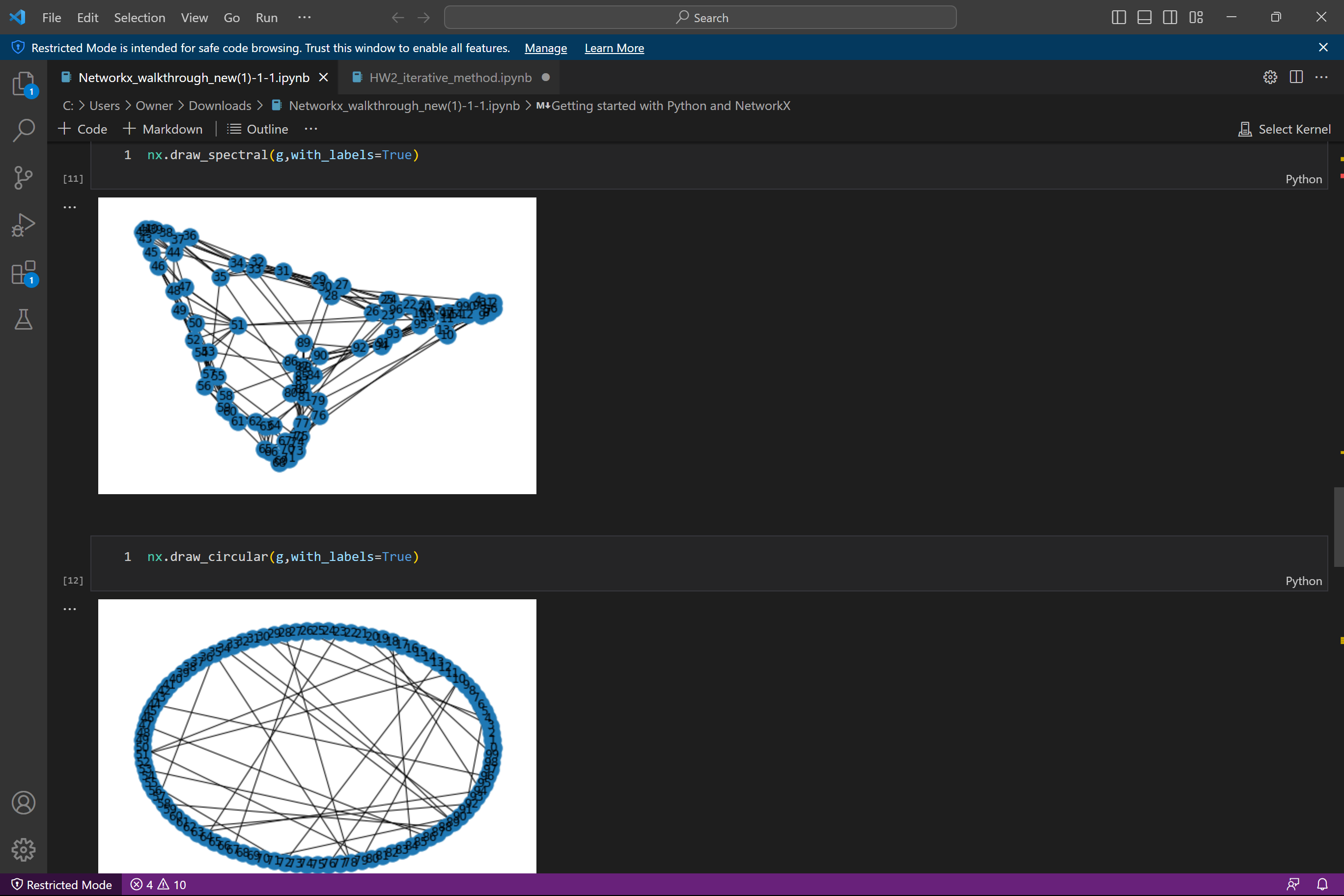
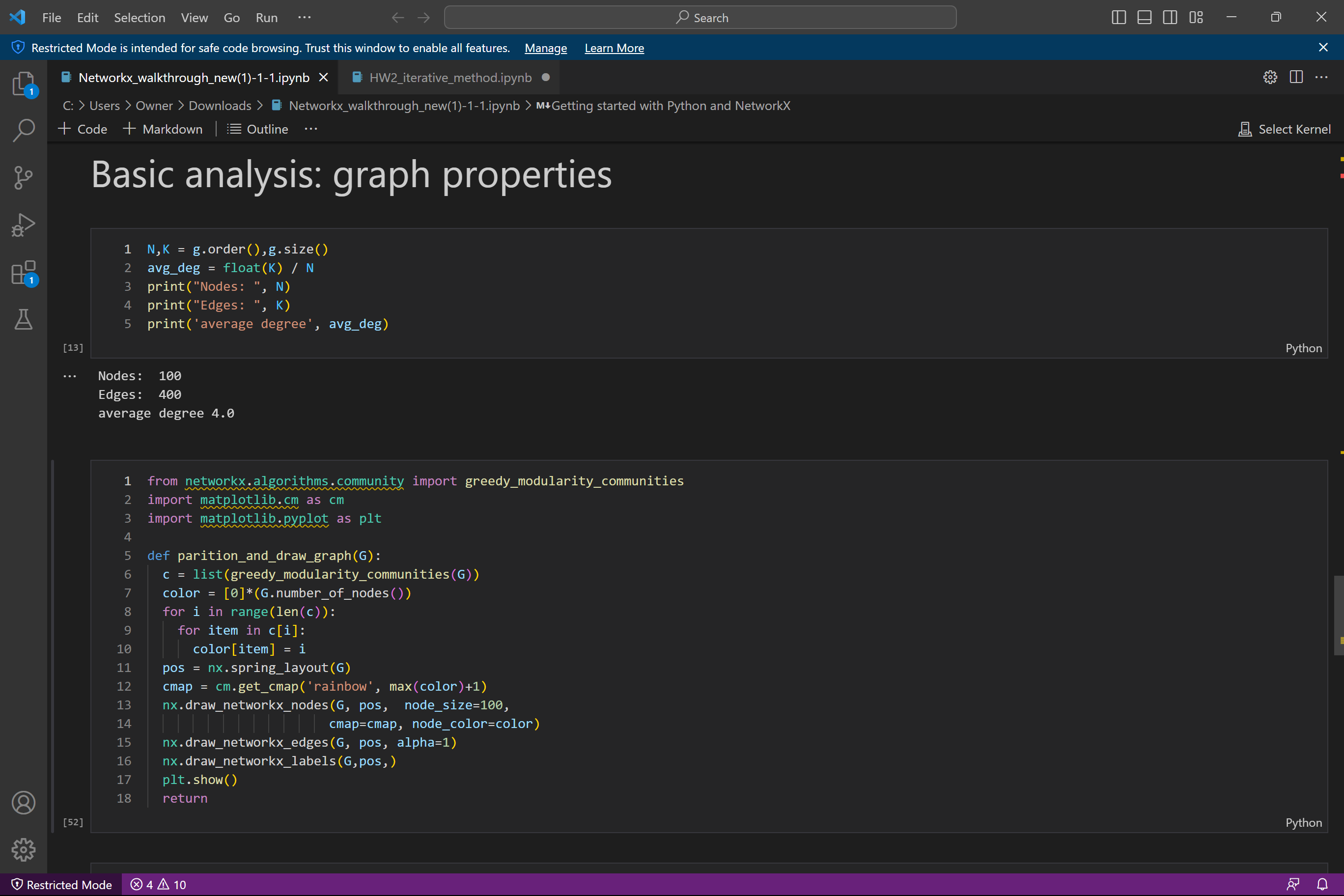
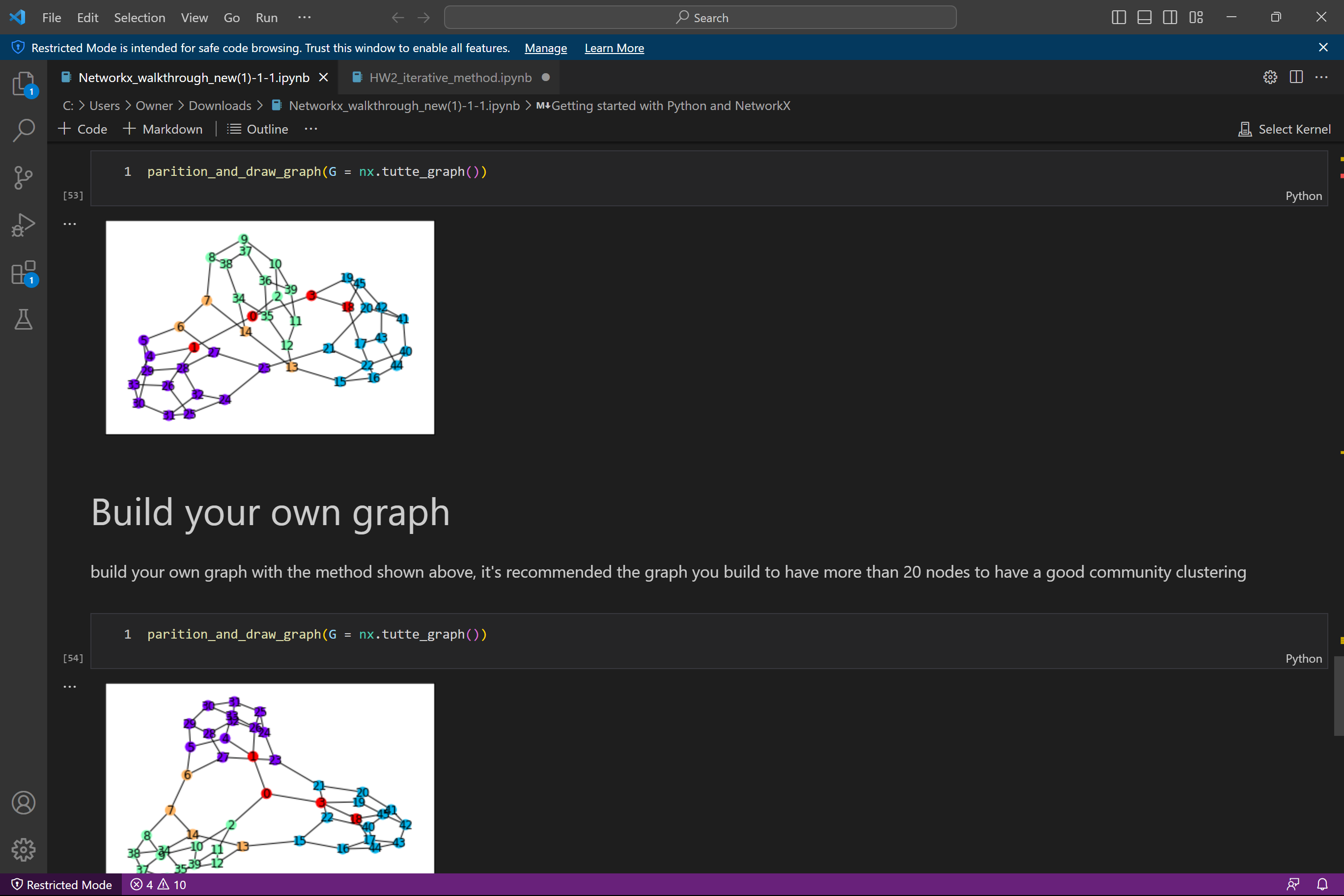
(I) Load a graph in terms of its adjacency matrix in Coo format. Construct the graph Laplacian matrix L. Compute its three smallest eigenvalues and corresponding eigenvectors 90, 91, 92. Disregard qo (which is the normalized constant vector). Embed the graph vertices in R using the rows of the matrix Q = [91, 92]. Then, for a given ne (a number smaller than n -the size of the graph), construct K = ne clusters (or aggregates) using the K-means algorithm. Write the relation "vertex-aggregate" as a nx ne sparse matrix P (it has nonzero values : 1 at row i and column j if vertex i belongs to aggregate j). - (II) Consider the s.p.d. matrix A = L + 0.01I ( a shifted graph Laplacian to make it s.p.d.). Implement the TL algorithm (description attached in separate file) BTL based on A, P, and Ac PT AP. = (III) Implement the preconditioned CG algorithm (description attached in separate file). Use the two-level preconditioner B BTL in the PCG to solve systems Ax = b. Some details about graphs and embedding are found on the following page. =