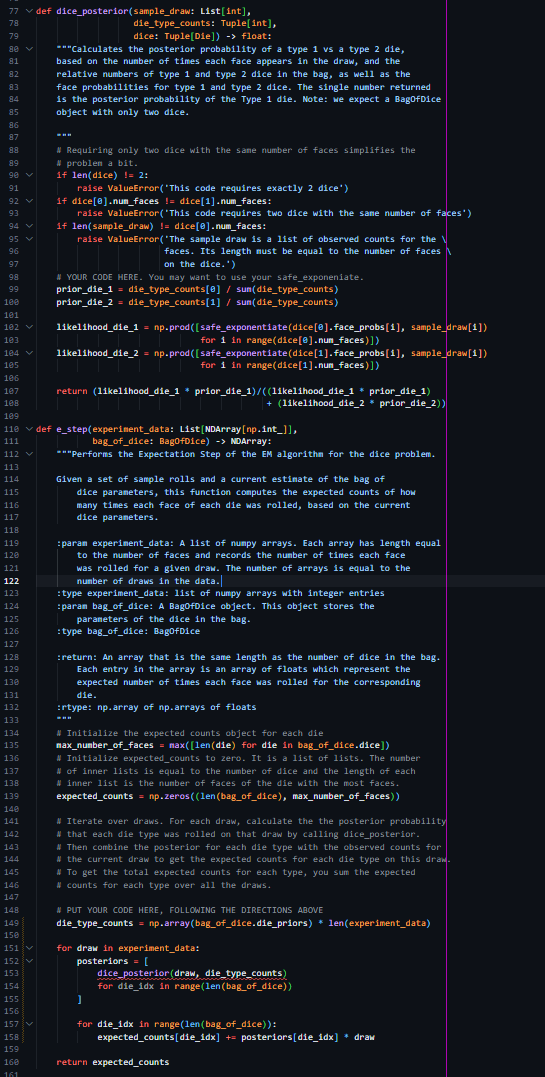
Question: I cant get the step _ e to work properly as seen in the photo def dice _ posterior ( sample _ draw: List [
I cant get the stepe to work properly as seen in the photo
def diceposteriorsampledraw: Listint
dietypecounts: Tupleint
dice: TupleDie float:
"Calculates the posterior probability of a type vs a type die,
based on the number of times each face appears in the draw, and the
relative numbers of type and type dice in the bag, as well as the
face probabilities for type and type dice. The single number returned
is the posterior probability of the Type die. Note: we expect a BagOfDice
object with only two dice.
Requiring only two dice with the sane number of faces simplifies the
problen a bit.
if lendice:
raise ValueErrorThis code requires exactly dice'
if dicenunfaces dicenumfaces:
raise ValueErrorThis code requires two dice with the same number of faces'
if lensampledraw dicenumfaces:
raise ValueErrorThe sample draw is a list of observed counts for the
faces. Its length nust be equal to the number of faces
on the dice.
yOUR CODE hERE. You may want to use your safeexponenate
priordie dietypecounts sumdietypecounts
priordie dietypecounts sumdietypecounts
ikelihooddie npprodsafeexponentiatedicefaceprobsi sampledrawi
for in rangedicenumfaces
likelihooddie npprodsafeexponentiatedicefaceprobs sampledraw
for in rangedicenumfaces
return likelihooddie priordielikelihooddie priordie
ikelihooddie priordie
def estepexperimentdata: ListNDArraynpint
bagofdice: BagofDice NDArray:
Performs the Expectation Step of the EM algorithm for the dice problem.
Given a set of sample rolls and a current estimate of the bag of
dice parameters, this function computes the expected counts of how
many times each face of each die was rolled, based on the current
dice parameters.
:paran experimentdata: A list of numpy arrays. Each array has length equal
to the number of faces and records the number of times each face
was rolled for a given draw. The number of arrays is equal to the
number of draws in the data.
:type experimentdata: list of numpy arrays with integer entries
:paran bagofdice: A BagofDice object. This object stores the
parameters of the dice in the bag.
:type bagofdice: BagOfDice
:return: An array that is the same length as the number of dice in the bag.
Each entry in the array is an array of floats which represent the
expected number of times each face was rolled for the corresponding
die.
:rtype: nparray of nparrays of floats
Initialize the expected counts object for each die
maxnumberoffaces maxlendie for die in bagofdice.dice
Initialize expectedcounts to zero. It is a list of lists. The number
wmathrm of inner lists is equal to the number of dice and the length of each
mathrm inner list is the number of faces of the die with the most faces.
expectedcounts npzeroslenbagofdice maxnumberoffaces
Iterate over draws. For each draw, calculate the the posterior probability
that each die type was rolled on that draw by calling diceposterior.
Then combine the posterior for each die type with the observed counts for
the current draw to get the expected counts for each die type on this dram.
To get the total expected counts for each type, you sum the expected
mathrm counts for each type over all the draws.
PUT YOUR CODE HERE, FOLLOWING THE DIRECTIONS ABOVE
dietypecounts nparraybagofdice.diepriors lenexperimentdata
for dray in experimentdata:
posteriors
diceposteriordraw dietypecounts
for dieidx in rangelenbagofdice
for dieidx in rangelenbagofdice:
expectedcountsdieidx posteriorsdieidx draw
return expectedcounts
Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


