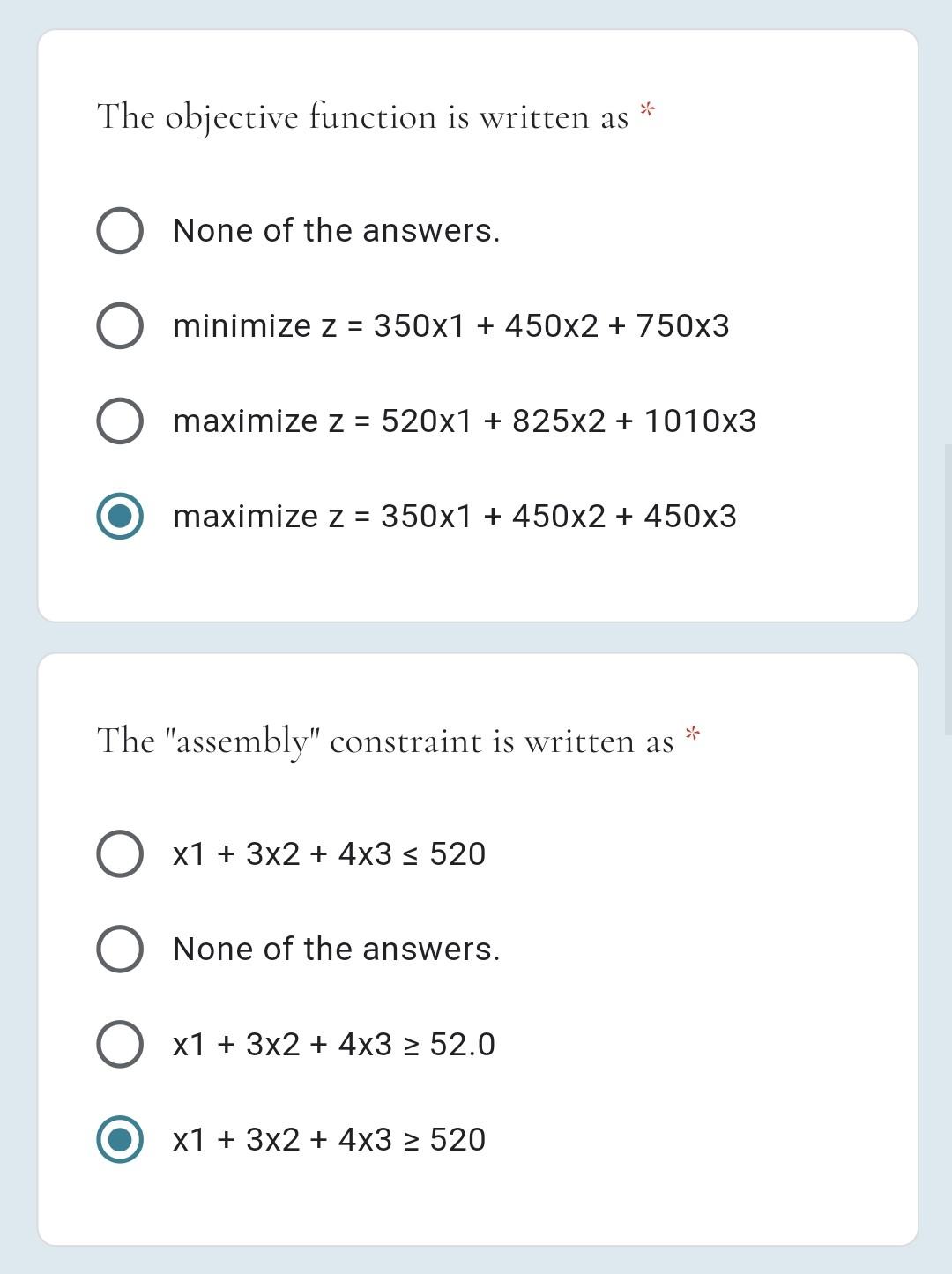
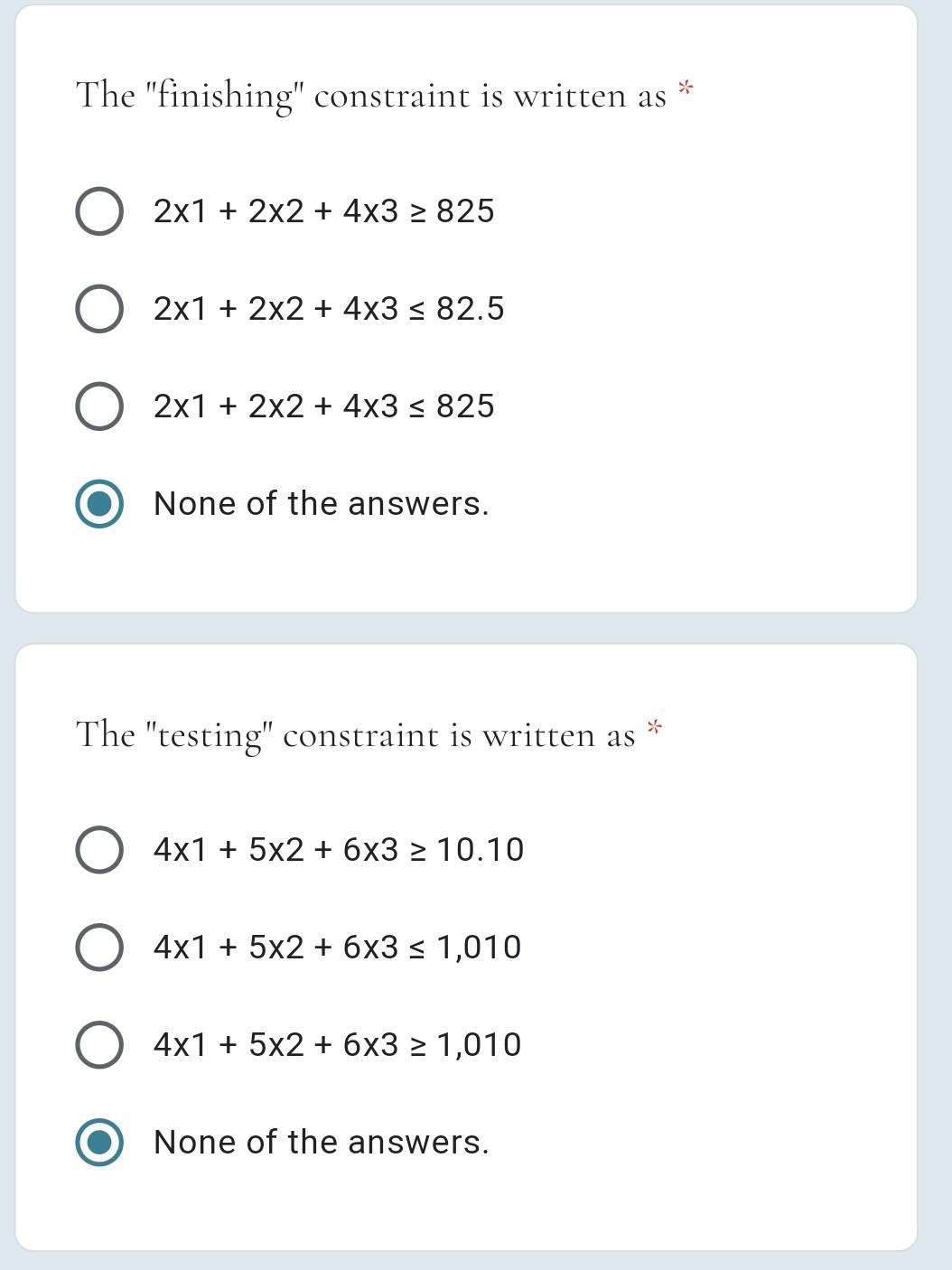
I. Formulation: Solve the following formulation problem. Consider the following problem: Apple must decide the production amounts of three types of products: "I-Phone", "I-Pad", & "Mac Book". An "I-Phone" costs $350, an "I-Pad" costs $450; and a MacBook'' costs $750. The manufacturing of an "I-Phone" requires 1 hour in assembly, 2 hours in finishing, and 4 hours in testing. The manufacturing of an I-Pad requires 3 hours in assembly, 2 hours in finishing, and 5 hours in testing The manufacturing of a "MacBook" requires 4 hours in assembly, 4 hours in finishing, and 6 hours in testing . The available times in the assembly, finishing, and testing departments are 520 hours, 825 hours, & 1010 hours, respectively, + C4: "I-Phones" and "I-Pads" production must be at least 30% of the total production. + C5: The total number of "I-Phones" should be at most twice the number of "I-Pads". To formulate a linear programming model, you a must All of the answers. Define the objective function Define the constraints Define the decision variables The decision variables of the the above problem are defined as * x1 = amount of "I-Phones" produced; x2 = amount of "I-Pads" produced; x3 = amount of "MacBooks" produced. = x1 = amount of "l-Phones" produced; x2 = amount of "l-Pads" produced; x3 = available hours in the assembly department. x1 = number of hours consumed in the "assembly" department, x2 = number of hours consumed in the "finishing" department; x3= number of hours consumed in the "testing" department. None of the answers. * The objective function is written as None of the answers. minimize z = 350x1 + 450x2 + 750x3 maximize z = 520x1 + 825x2 + 1010x3 maximize z = 350x1 + 450x2 + 450x3 * The "assembly" constraint is written as x1 + 3x2 + 4x3 = 520 O None of the answers. x1 3x2 + 4x3 > 52.0 x1 + 3x2 + 4x3 > 520 * The "finishing" constraint is written as 2x1 + 2x2 + 4x3 > 825 2x1 + 2x2 + 4x3 = 82.5 2x1 + 2x2 + 4x3 = 825 None of the answers. The "testing" constraint is written as 4x1 + 5x2 + 6x3 2 10.10 4x1 + 5x2 + 6x3 = 1,010 4x1 + 5x2 + 6x3 > 1,010 None of the answers