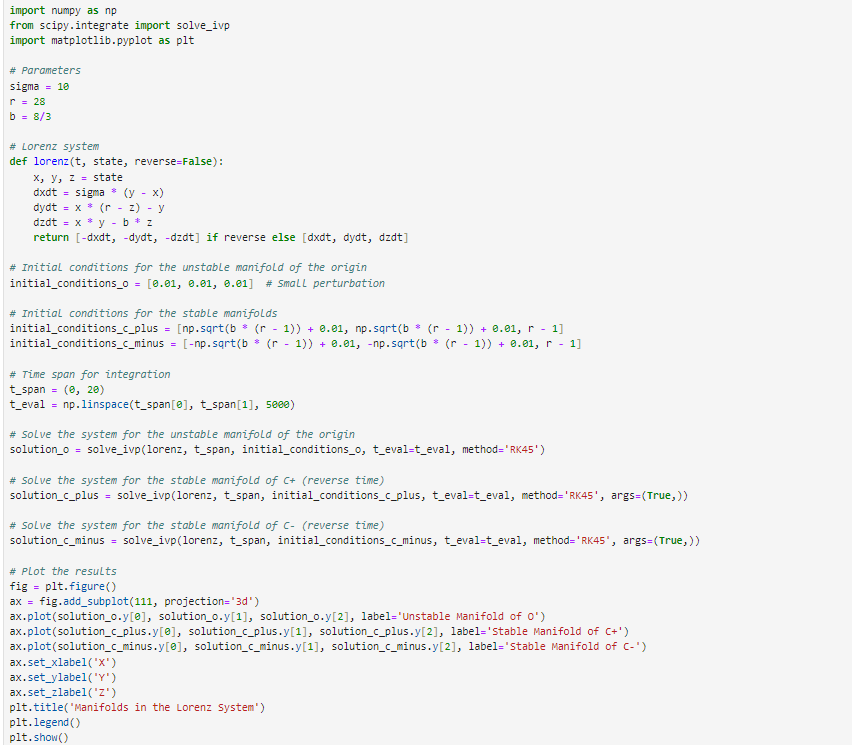
I have been trying to execute this code but it won't produce any output no matter what I need to get the figures I am trying to show down here import numpy as np from scipy integrate import solve ivp import matplotlib pyplot as plt Parameters sigma 1 0 r 2 8 b 8 3 Lorenz system def lorenz ( t , state, reverse False ) x , y , z state dxdt sigma ( y x ) dydt x ( r z ) y dzdt x y b z return dxdt , dydt , dzdt if reverse else dxdt , dydt , dzdt Initial conditions for the unstable manifold of the origin initial conditions o 0 0 1 , 0 0 1 , 0 0 1 Small perturbation Initial conditions for the stable manifolds initial conditions c plus np sqrt ( b ( r 1 ) ) 0 0 1 , np sqrt ( b ( r 1 ) ) 0 0 1 , r 1 initial conditions c minus np sqrt ( b ( r 1 ) ) 0 0 1 , np sqrt ( b ( r 1 ) ) 0 0 1 , r 1 Time span for integration t span ( 0 , 5 0 ) t eval np linspace ( t span 0 , t span 1 , 1 0 0 0 0 ) Solve the system for the unstable manifold of the origin solution o solve ivp ( lorenz , t span, initial conditions o , t eval t eval, method ' RK 4 5 ' ) Solve the system for the stable manifold of C ( reverse time ) solution c plus solve ivp ( lorenz , t span, initial conditions c plus, t eval t eval, method ' RK 4 5 ' , args ( True , ) ) Solve the system for the stable manifold of C ( reverse time ) solution c minus solve ivp ( lorenz , t span, initial conditions c minus, t eval t eval, method ' RK 4 5 ' , args ( True , ) ) Plot the results fig plt figure ( ) ax fig add subplot ( 1 1 1 , projection ' 3 d ' ) ax plot ( solution o y 0 , solution o y 1 , solution o y 2 , label 'Unstable Manifold of O ' ) ax plot ( solution c plus y 0 , solution c plus y 1 , solution c plus y 2 , label 'Stable Manifold of C ' ) ax plot ( solution c minus y 0 , solution c minus y 1 , solution c minus y 2 , label 'Stable Manifold of C ' ) ax set xlabel ( ' X ' ) ax set ylabel ( ' Y ' ) ax set zlabel ( ' Z ' ) plt title ( ' Manifolds in the Lorenz System' ) plt legend ( ) plt show ( ) import numpy as np from scipy integrate import solve ivp import matplotlib pyplot as plt Parameters sigma 1 0 r 2 8 b 8 3 Lorenz system def lorenz ( t , state, reverse False ) x , y , z state dxdt sigma ( y x ) dydt x ( r z ) y dzdt x y b z return dxdt , dydt , dzdt if reverse else dxdt , dydt , dzdt Initial conditions for the unstable manifold of the origin initial conditions 0 0 0 1 , 0 0 1 , 0 0 1 Small perturbation Initial conditions for the stable manifolds initial conditions c plus np sqrt ( b ( r 1 ) ) 0 0 1 , np sqrt ( b ( r 1 ) ) 0 0 1 , r 1 initial conditions c minus np sqrt ( b ( r 1 ) ) 0 0 1 , np sqrt ( b ( r 1 ) ) 0 0 1 , r 1 Time span for integration t span ( 0 , 2 0 ) t eval np linspace ( t span 0 , t span 1 , 5 0 0 0 ) Solve the system for the unstable manifold of the origin solution 0 solve ivp ( lorenz , t span, initial conditions o , t eval t eval, method ' RK 4 5 ' ) Solve the system for the stable manifold of C ( reverse time ) solution c plus solve ivp ( lorenz , t span, initial conditions c plus, t eval t eval, method ' RK 4 5 ' , args ( True , ) ) Solve the system for the stable manifold of C ( reverse time ) solution c minus solve ivp ( lorenz , t span, initial conditions c minus, t eval t eval, method ' RK 4 5 ' , args ( True , ) ) Plot the results fig plt figure ( ) ax fig add subplot ( 1 1 1 , projection ' 3 d ' ) ax plot ( solution o y 0 , solution o y 1 , solution o y 2 , label 'Unstable Manifold of 0 ' ) ax plot ( solution c plus y 0 , solution c plus y 1 , solution c plus y 2 , label 'stable Manifold of C ' ) ax plot ( solution c minus y 0 , solution c minus y 1 , solution c minus y 2 , label 'stable Manifold of C ' ) ax set xlabel ( ' X ' ) ax set ylabel ( ' Y ' ) ax set zlabel ( ' Z ' ) plt title ( ' Manifolds in the Lorenz System' ) plt legend ( ) plt show ( )

The Answer is in the image, click to view ...

Question: I have been trying to execute this code but it won't produce any output no matter what. I need to get the figures I am

I have been trying to execute this code but it won't produce any output no matter what. I need to get the figures I am trying to show down here:

import numpy as np

from scipy.integrate import solve

_

ivp

import matplotlib.pyplot as plt

# Parameters

sigma

= 10

= 28

= 8 / 3

# Lorenz system

def lorenz

(

,

state, reverse

=

False

)

,

,

=

state

dxdt

=

sigma

* (

-

)

dydt

=

* (

-

) -

dzdt

=

*

-

*

return

[-

dxdt

, -

dydt

, -

dzdt

]

if reverse else

[

dxdt

,

dydt

,

dzdt

]

# Initial conditions for the unstable manifold of the origin

initial

_

conditions

_

= [0.01, 0.01, 0.01]

# Small perturbation

# Initial conditions for the stable manifolds

initial

_

conditions

_

_

plus

= [

.

sqrt

(

* (

- 1)) + 0.01,

.

sqrt

(

* (

- 1)) + 0.01,

- 1]

initial

_

conditions

_

_

minus

= [-

.

sqrt

(

* (

- 1)) + 0.01, -

.

sqrt

(

* (

- 1)) + 0.01,

- 1]

# Time span for integration t

_

span

= (0, 50)

_

eval

=

.

linspace

(

_

span

[0],

_

span

[1], 10000)

# Solve the system for the unstable manifold of the origin

solution

_

=

solve

_

ivp

(

lorenz

,

_

span, initial

_

conditions

_

,

_

eval

=

_

eval, method

='

45')

# Solve the system for the stable manifold of C

+ (

reverse time

)

solution

_

_

plus

=

solve

_

ivp

(

lorenz

,

_

span, initial

_

conditions

_

_

plus, t

_

eval

=

_

eval, method

='

45',

args

= (

True

,))

# Solve the system for the stable manifold of C

- (

reverse time

)

solution

_

_

minus

=

solve

_

ivp

(

lorenz

,

_

span, initial

_

conditions

_

_

minus, t

_

eval

=

_

eval, method

='

45',

args

= (

True

,))

# Plot the results fig

=

plt

.

figure

()

=

fig.add

_

subplot

(111,

projection

=' 3

')

.

plot

(

solution

_

.

[0],

solution

_

.

[1],

solution

_

.

[2],

label

=

'Unstable Manifold of O

')

.

plot

(

solution

_

_

plus.y

[0],

solution

_

_

plus.y

[1],

solution

_

_

plus.y

[2],

label

=

'Stable Manifold of C

+')

.

plot

(

solution

_

_

minus.y

[0],

solution

_

_

minus.y

[1],

solution

_

_

minus.y

[2],

label

=

'Stable Manifold of C

-')

.

set

_

xlabel

('

')

.

set

_

ylabel

('

')

.

set

_

zlabel

('

')

plt

.

title

('

Manifolds in the Lorenz System'

)

plt

.

legend

()

plt

.

show

() ` ` `

import numpy as np

from scipy.integrate import solve

_

ivp

import matplotlib.pyplot as plt

# Parameters

sigma

= 10

= 28

= 8 / 3

# Lorenz system

def lorenz

(

,

state, reverse

=

False

)

,

,

=

state

dxdt

=

sigma

* (

-

)

dydt

=

* (

-

) -

dzdt

=

*

-

*

return

[-

dxdt

, -

dydt

, -

dzdt

]

if reverse else

[

dxdt

,

dydt

,

dzdt

]

# Initial conditions for the unstable manifold of the origin

initial

_

conditions

_0 = [0.01, 0.01, 0.01]

# Small perturbation

# Initial conditions for the stable manifolds

initial

_

conditions

_

_

plus

= [

.

sqrt

(

* (

- 1)) + 0.01,

.

sqrt

(

* (

- 1)) + 0.01,

- 1]

initial

_

conditions

_

_

minus

= [-

.

sqrt

(

* (

- 1)) + 0.01, -

.

sqrt

(

* (

- 1)) + 0.01,

- 1]

# Time span for integration

_

span

= (0, 20)

_

eval

=

.

linspace

(

_

span

[0],

_

span

[1], 5000)

# Solve the system for the unstable manifold of the origin

solution

_0 =

solve

_

ivp

(

lorenz

,

_

span, initial

_

conditions

_

,

_

eval

=

_

eval, method

='

45')

# Solve the system for the stable manifold of C

+ (

reverse time

)

solution

_

_

plus

=

solve

_

ivp

(

lorenz

,

_

span, initial

_

conditions

_

_

plus, t

_

eval

=

_

eval, method

='

45',

args

= (

True

,))

# Solve the system for the stable manifold of C

- (

reverse time

)

solution

_

_

minus

=

solve

_

ivp

(

lorenz

,

_

span, initial

_

conditions

_

_

minus, t

_

eval

=

_

eval, method

='

45',

args

= (

True

,))

# Plot the results

fig

=

plt

.

figure

()

=

fig.add

_

subplot

(111,

projection

=' 3

')

.

plot

(

solution

_

.

[0],

solution

_

.

[1],

solution

_

.

[2],

label

=

'Unstable Manifold of

0')

.

plot

(

solution

_

_

plus.y

[0],

solution

_

_

plus.y

[1],

solution

_

_

plus.y

[2],

label

=

'stable Manifold of C

+')

.

plot

(

solution

_

_

minus.y

[0],

solution

_

_

minus.y

[1],

solution

_

_

minus.y

[2],

label

=

'stable Manifold of C

-')

.

set

_

xlabel

('

')

.

set

_

ylabel

('

')

.

set

_

zlabel

('

')

plt

.

title

('

Manifolds in the Lorenz System'

)

plt

.

legend

()

plt

.

show

()

` ` `

I have been trying to execute this code but it

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Programming Questions!

In C++ please. Assignment 4 This assignment is the first in a sequence of three. It is not strictly necessary to complete this one in order to do the other two, but the understanding you gain in...

Purpose: To give you experience implementing and using linked data structures. Goal 1: To design and implement a class LinkedDS that will act as a linked data structure for accessing Java Objects....

Assignment #1: Class Associations & Interfaces Due Date: Monday, February 22nd at 11:59 PM (2 weeks) Introduction This semester we will study object-oriented graphics programming and design by...

Program 2 - Advanced Automobile Objects Please do in C++ This program is made to go off of a lab we previously did which is below. Header file: AutoTypeImp File: Main File: CSC1720 Program 2 -...

First, uncomment the following block of code, by removing all of the \# symbols before each line. You can do this quickly if you're using VS Code by selecting the entire block of code, going into the...

This shell program is in C and a complete solution to the problem except for handling the > operators is provided below. You may use any or all of this code in your solution to this...

This is in C and a complete solution to the problem except for handling the > operators is provided below. You may use any or all of this code in your solution to this assignment. Thanks in...

This assignment is intended to make you do a lot of work with dynamic memory allocation, pointers, and arrays of pointers. Don\'t wait until the weekend it\'s due to start it! Your solution should...

NEED IT ASAP PLSSSSSSS 1 Introduction and purpose In this project you will write some functions to manipulate the instructions of a fictional simple processor named the MAD Raisin. The MAD Raisin CPU...

Using the Conceptual Framework Model, analyze the Hayden Tool Company Case. Be sure to evaluate all internal and external environment factors and scans. If a factor does not impact this case, be sure...

One of the biological pathways by which an amine is converted to a ketone involves two steps: (1) oxidation of the amine by NAD+ to give an imine, and (2) hydrolysis of the imine to give a ketone...

1. An officer of Westway Corporation recently commented that when he receives the firms financial statements, he looks at just the bottom line of the income statementthe line that shows the net...

Garden Variety Flower Shop uses 710 clay pots a month. The pots are purchased at $ \$ 2.20 $ each. Annual carrying costs per pot are estimated to be 50 percent of cost, and ordering costs are \( \$