I just need help finding the second to last answer. Thank you!

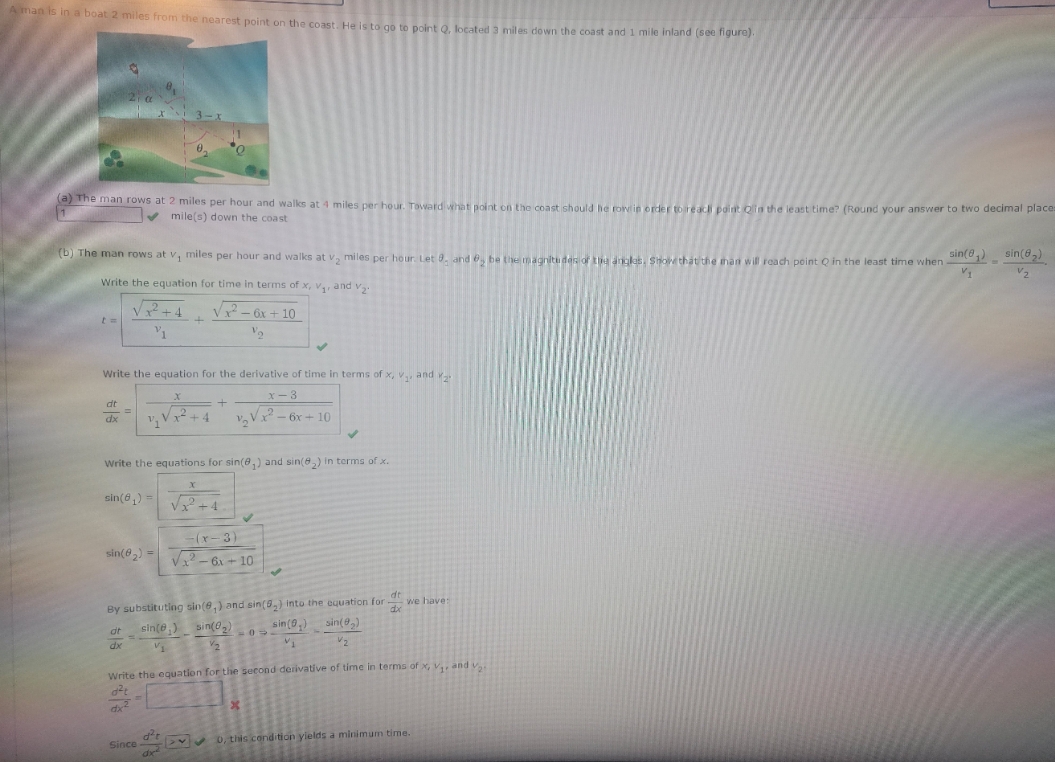
A man is in a boat 2 miles from the nearest point on the coast. He is to go to point Q, located 3 miles down the coast and 1 mile inland (see figure). 1 mile(s) down the coast (a) The man rows at 2 miles per hour and walks at 4 miles per hour. Toward what point on the coast should he row in order to reach point Qlin the least time? (Round your answer to two decimal place (D) The man rows at v, miles per hour and walks at v2 miles per hour. Let 8, and 6, be the magnitudes of the angles, Show that the man will reach point Q in the least time when - sin(8,) _sin(82) V1 V 2 Write the equation for time in terms of x, V, , and v2. Vx 2+4 Vx -6x + 10 Write the equation for the derivative of time in terms of x, v, , and 2. x - 3 V V x 2 + 4 v, Vx - 6x + 10 Write the equations for sin(8, ) and sin(8) In terms of x. sin(6 ) = Vx2 + 4 -(x - 3) sin(82) = V12 -6x + 10 By substituting sin(8, ) and sin (8, ) into the equation for - we have: sin(8,) _sin(82) sin(0,) sin( 82) V 1 V2 Write the equation for the second derivative of time in terms of *, V1, and v2. d't Since 2 0, this condition yields a minimum time