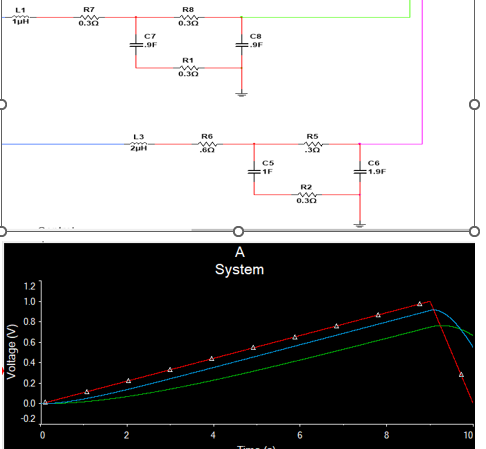
i need a simulink subsystem step by step about modify $3$ equations integro diferential about that circuit please this is a example of the same circuit except $1$ less electrical resistence $\backslash$subsection$\{$Ecuaciones principales$\}$

$\backslash$bigskip Dentro de este apartado, encontramos $3$ ecuaciones, las cuales son:

Ecuaci$\backslash \text{'}\{$o$\}$n de voltaje de entrada, igualdad de voltaje y voltaje de saida.

$\backslash$begin$\{$eqnarray$*\}$

P$\_\{$ao$\}\backslash$left$($ t$\backslash$right$)$ &$=$&L$\backslash$frac$\{$di$\_\{1\}\backslash$left$($ t$\backslash$right$)\}\{$dt$\}+$R$\_\{1\}$i$\_\{1\}\backslash$left$($

t$\backslash$right$)+\backslash$frac$\{1\}\{$C$\_\{1\}\}\backslash$int $\backslash$left$[$ i$\_\{1\}\backslash$left$($ t$\backslash$right$)-$i$\_\{2\}\backslash$left$($

t$\backslash$right$)\backslash$right$]$ dt $\backslash \backslash$

$\backslash$frac$\{1\}\{$C$\_\{1\}\}\backslash$int $\backslash$left$[$ i$\_\{1\}\backslash$left$($ t$\backslash$right$)-$i$\_\{2\}\backslash$left$($ t$\backslash$right$)\backslash$right$]$

dt &$=$&R$\_\{2\}$i$\_\{2\}\backslash$left$($ t$\backslash$right$)+\backslash$frac$\{1\}\{$C$\_\{2\}\}\backslash$int i$\_\{2\}\backslash$left$($ t$\backslash$right$)$ dt

$\backslash \backslash$

P$\_\{$p$\}\backslash$left$($ t$\backslash$right$)$ &$=$&$\backslash$frac$\{1\}\{$C$\_\{2\}\}\backslash$int i$\_\{2\}\backslash$left$($ t$\backslash$right$)$ dt

$\backslash$end$\{$eqnarray$*\}$

$\backslash$subsection$\{$Ecuaciones integrodiferenciales$\}$

$\backslash$bigskip Despejamos $i$\_\{1\}$$

$\backslash$begin$\{$eqnarray$*\}$

P$\_\{$ao$\}\backslash$left$($ t$\backslash$right$)$ &$=$&L$\backslash$frac$\{$di$\_\{1\}\backslash$left$($ t$\backslash$right$)\}\{$dt$\}+$R$\_\{1\}$i$\_\{1\}\backslash$left$($

t$\backslash$right$)+\backslash$frac$\{1\}\{$C$\_\{1\}\}\backslash$int $\backslash$left$[$ i$\_\{1\}\backslash$left$($ t$\backslash$right$)-$i$\_\{2\}\backslash$left$($

t$\backslash$right$)\backslash$right$]$ dt $\backslash \backslash$

R$\_\{1\}$i$\_\{1\}\backslash$left$($ t$\backslash$right$)$ &$=$&V$\_\{$e$\}\backslash$left$($ t$\backslash$right$)-$L$\backslash$frac$\{$di$\_\{1\}\backslash$left$($

t$\backslash$right$)\}\{$dt$\}-\backslash$frac$\{1\}\{$C$\_\{1\}\}\backslash$int $\backslash$left$[$ i$\_\{1\}\backslash$left$($ t$\backslash$right$)-$i$\_\{2\}\backslash$left$($

t$\backslash$right$)\backslash$right$]$ dt $\backslash \backslash$

i$\_\{1\}\backslash$left$($ t$\backslash$right$)$ &$=$&$\backslash$left$[$ P$\_\{$ao$\}\backslash$left$($ t$\backslash$right$)-$L$\backslash$frac$\{$di$\_\{1\}\backslash$left$($

t$\backslash$right$)\}\{$dt$\}-\backslash$frac$\{1\}\{$C$\_\{1\}\}\backslash$int $\backslash$left$[$ i$\_\{1\}\backslash$left$($ t$\backslash$right$)-$i$\_\{2\}\backslash$left$($

t$\backslash$right$)\backslash$right$]$ dt$\backslash$right$]\backslash$frac$\{1\}\{$R$\_\{1\}\}$

$\backslash$end$\{$eqnarray$*\}$

$\backslash$bigskip $\backslash$bigskip Despejamos $i$\_\{2\}$$

$\backslash$begin$\{$eqnarray$*\}$

$\backslash$frac$\{1\}\{$C$\_\{1\}\}\backslash$int $\backslash$left$[$ i$\_\{1\}\backslash$left$($ t$\backslash$right$)-$i$\_\{2\}\backslash$left$($ t$\backslash$right$)\backslash$right$]$

dt &$=$&R$\_\{2\}$i$\_\{2\}\backslash$left$($ t$\backslash$right$)+\backslash$frac$\{1\}\{$C$\_\{2\}\}\backslash$int i$\_\{2\}\backslash$left$($ t$\backslash$right$)$ dt

$\backslash \backslash$

R$\_\{2\}$i$\_\{2\}\backslash$left$($ t$\backslash$right$)$ &$=$&$\backslash$frac$\{1\}\{$C$\_\{1\}\}\backslash$int $\backslash$left$[$ i$\_\{1\}\backslash$left$($ t$\backslash$right$)$

$-$i$\_\{2\}\backslash$left$($ t$\backslash$right$)\backslash$right$]$ dt$-\backslash$frac$\{1\}\{$C$\_\{2\}\}\backslash$int i$\_\{2\}\backslash$left$($ t$\backslash$right$)$ dt

$\backslash \backslash$

i$\_\{2\}\backslash$left$($ t$\backslash$right$)$ &$=$&$\backslash$left$[\backslash$frac$\{1\}\{$C$\_\{1\}\}\backslash$int $\backslash$left$[$ i$\_\{1\}\backslash$left$($

t$\backslash$right$)-$i$\_\{2\}\backslash$left$($ t$\backslash$right$)\backslash$right$]$ dt$-\backslash$frac$\{1\}\{$C$\_\{2\}\}\backslash$int i$\_\{2\}\backslash$left$($

t$\backslash$right$)$ dt$\backslash$right$]\backslash$frac$\{1\}\{$R$\_\{2\}\}$

$\backslash$end$\{$eqnarray$*\}$

$\backslash$bigskip

$\backslash$begin$\{$equation$*\}$

P$\_\{$p$\}\backslash$left$($ t$\backslash$right$)=\backslash$frac$\{1\}\{$C$\_\{2\}\}\backslash$int i$\_\{2\}\backslash$left$($ t$\backslash$right$)$ dt

$\backslash$end$\{$equation$*\}$

$\backslash$subsection$\{$Transformada de Laplace$\}$

$\backslash$bigskip

$\backslash$begin$\{$eqnarray$*\}$

P$\_\{$ao$\}\backslash$left$($ s$\backslash$right$)$ &$=$&LsI$\_\{1\}\backslash$left$($ s$\backslash$right$)+$R$\_\{1\}$I$\_\{1\}\backslash$left$($ s$\backslash$right$)+\%$

$\backslash$frac$\{$I$\_\{1\}\backslash$left$($ s$\backslash$right$)-$I$\_\{2\}\backslash$left$($ s$\backslash$right$)\}\{$C$\_\{1\}$s$\}\backslash \backslash$

$\backslash$frac$\{1\}\{$C$\_\{1\}$s$\}\backslash$left$[$ I$\_\{1\}\backslash$left$($ s$\backslash$right$)-$I$\_\{2\}\backslash$left$($ s$\backslash$right$)\backslash$right$]$

&$=$&$\backslash$left$($ R$\_\{2\}+\backslash$frac$\{1\}\{$C$\_\{2\}$s$\}\backslash$right$)$ I$\_\{2\}\backslash$left$($ s$\backslash$right$)\backslash \backslash$

P$\_\{$p$\}\backslash$left$($ s$\backslash$right$)$ &$=$&$\backslash$frac$\{$I$\_\{2\}\backslash$left$($ s$\backslash$right$)\}\{$C$\_\{2\}$s$\}$

$\backslash$end$\{$eqnarray$*\}$