I need answer for part d specifically. But if you can solve the entire problem that will be nice too, I will check if I have done other parts correctly. But I don't know how to solve PART D

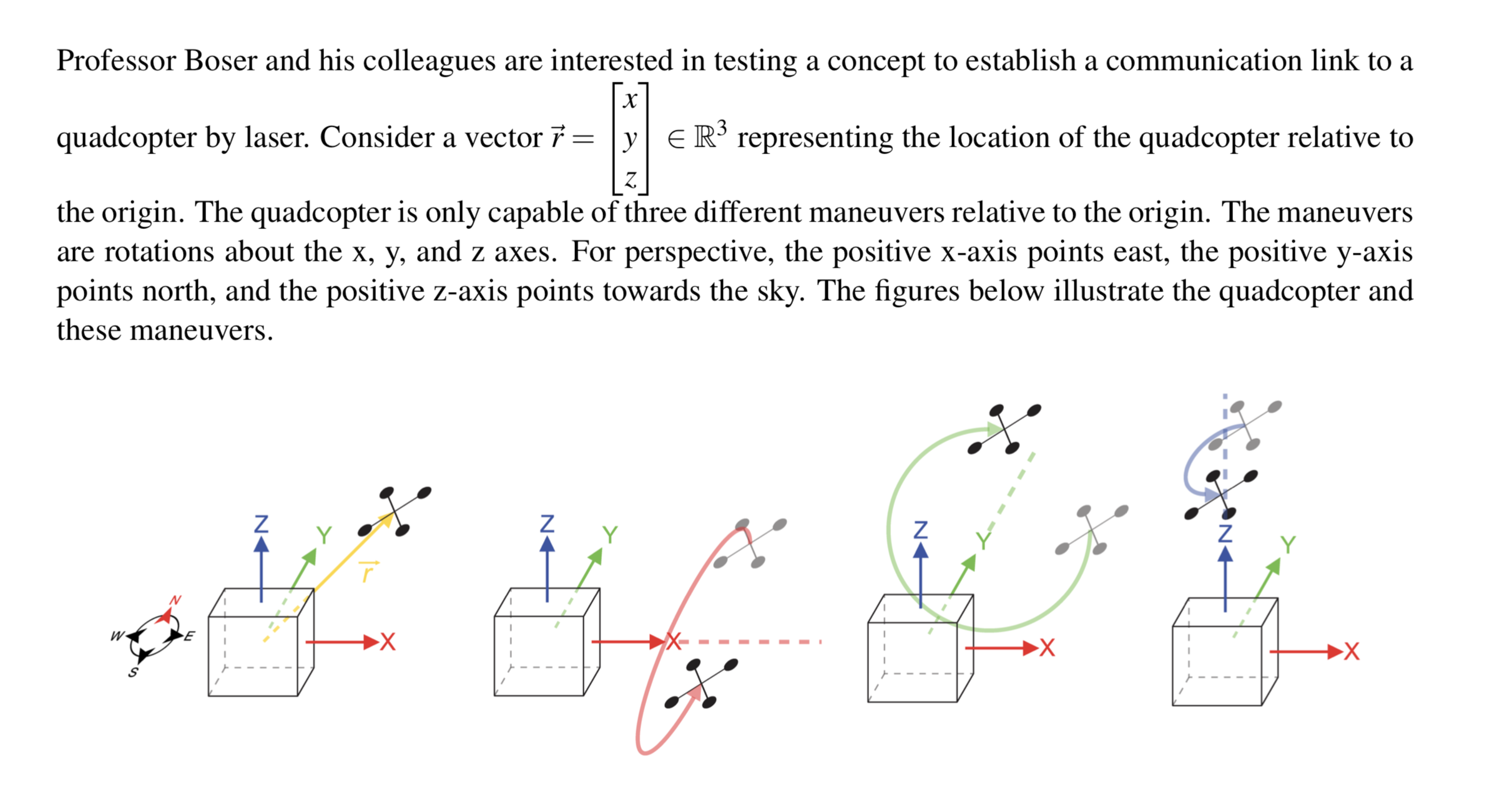
Professor Boser and his colleagues are interested in testing a concept to establish a communication link to a x quadcopter by laser. Consider a vector 7 = y E R3 representing the location of the quadcopter relative to z the origin. The quadcopter is only capable of three different maneuvers relative to the origin. The maneuvers are rotations about the x, y, and z axes. For perspective, the positive x-axis points east, the positive y-axis points north, and the positive z-axis points towards the sky. The gures below illustrate the quadcopter and these maneuvers. We can represent each of these rotations, that are linear transformations, as matrices that operate on the location vector of the quadcopter, r, to position it at it's new location. The matrices Rx(0), Ry(y), and Rz($ ) represent rotations about the x-axis, y-axis, and z-axis, respectively. The matrices are: 0 0 cosy 0 - sin ys cos - sin RX ( 0) = cos e - sin 0 , Ry(y) = 0 0 , Rz($ ) = sin o COs Q sin 0 cos 0 sin ys 0 cosy 0 0 (a) Professor Boser wants to make the quadcopter to rotate first by 30 about the x-axis, and then by 60 about the z-axis. Use Rx(0), Ry(y), and Rz( ) to construct a matrix that performs the operations in the specified order. You may use an ipython notebook for algebra, but show in your solutions the matrices and the operations you are doing on them by hand. (b) Professor Boser accidentally punched in the two commands in reverse. The rotation about the z-axis occurred before the rotation about the x-axis. Use Rx(0), Ry(y), and Rz($ ) to construct a matrix that performs the operations that accidentally happened. You may use an ipython notebook for algebra. Write out the matrices you are multiplying, and the computed matrix. (c) Say the quadcopter was at 7 = Where did Professor Boser intend for the quadcopter to end up? Where did it actually end up? Are they the same? (d) Say the quadcopter starts out at distance 1 from the origin, i.e. | || | = 1. Say Professor Boser performs an arbitrary sequence of operations (unknown to you) using the three transformation matrices Rx (0), Ry( y), and Rz(). Each transformation could be used more than once. Then the quadcopter ends up at location s. What is | |51|