I need help explaining this quantitatively. What I imagine needs to be done is to show that the time between the events in the rod's reference frame $($which are simultaneous in the barn's reference frame$)$ is equal to the time required for it to pass through the door, but i don$$t know exactly how to do the calculations.

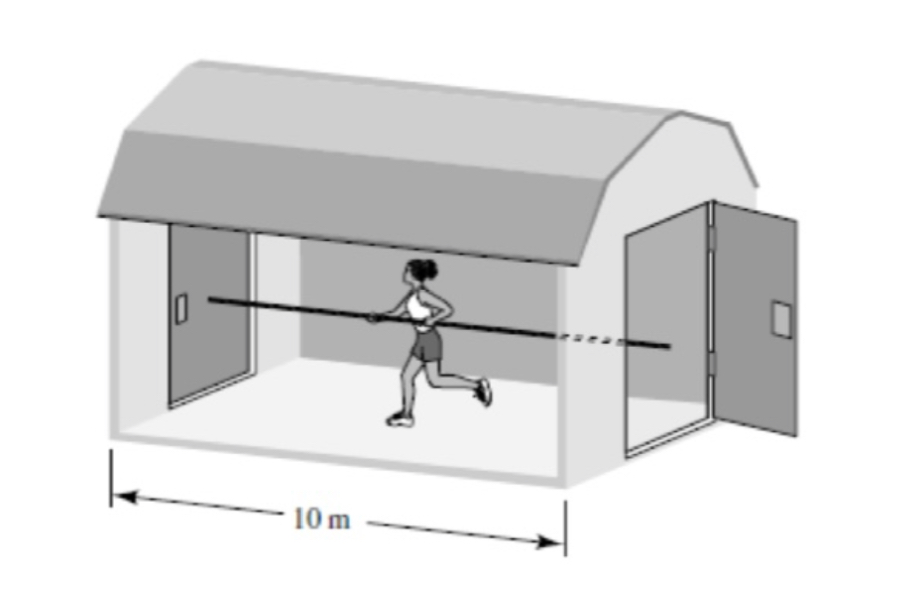
$1)$ A rod of $20$ m is carried with such a high velocity in the direction of its length that it appears to have only $10$ m of length in the reference frame of the barn. The runner carries the rod through the front door of a barn that is $10$ m long. At the exact moment when the end of the rod reaches the back door, opposite to the front door, the front door is closed so that it fully contains the $10$ m rod inside the barn for an instant. At this moment, the back door is opened, and the runner crosses the barn. From the point of view of the rod, its length is $20$ m$,$ while the barn is only $5$ m long! Thus, the rod could never be entirely inside the barn. Explain, quantitatively and through space$-$time diagrams, this apparent paradox.