i need help filling put the blanks in table 3 and the last two questions ASAP

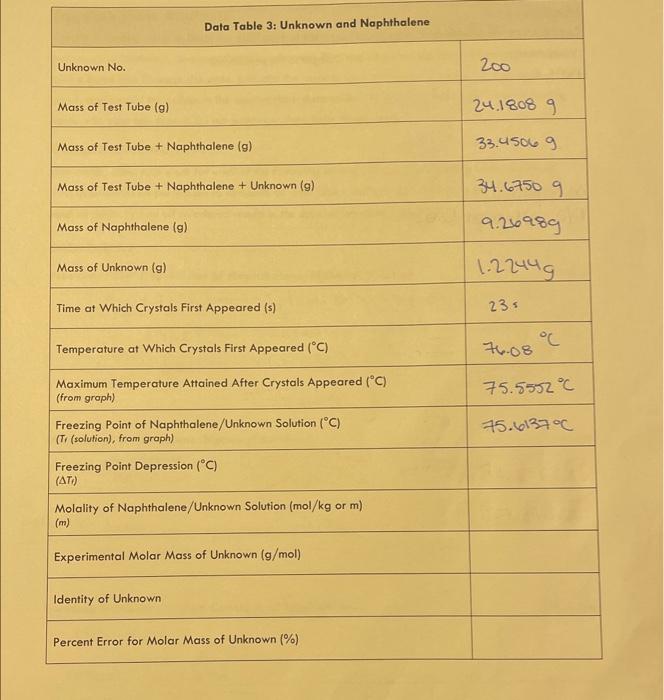
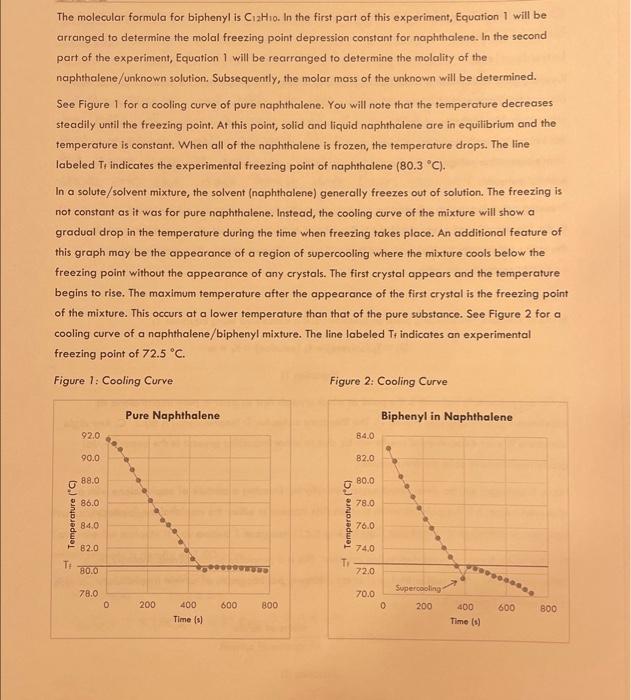
Data Table 3: Unknown and Naphthalene Unknown No. Mass of Test Tube (g) 24.18089 Mass of Test Tube + Naphthalene (g) 33.4506.9 Mass of Test Tube + Naphthalene + Unknown (g) 34.67509 Mass of Naphthalene (g) 9.26989 Mass of Unknown (g) 1.2249 Time at Which Crystals First Appeared (s) 23= Temperature at Which Crystals First Appeared (C) Maximum Temperature Attained After Crystals Appeared (C) (from groph) Freezing Point of Naphthalene/Unknown Solution (C) (Tr (solution), from graph) Freezing Point Depression ( C ) ( Ti) Molality of Naphthalene/Unknown Solution ( mol/kg or m ) (m) Experimental Molar Mass of Unknown (g/mol) Identity of Unknown Percent Error for Molar Mass of Unknown (\%) Sample Calculations (For credit, show your work for each of the following sample calculations, including units. Additional calculations must be performed to complete all data tables, but you do not have to show a sample of each of these. Record all calculated results in the appropriote data table.) DATA TABLE 2 Freezing Point Depression of Naphthalene/Biphenyl Solution f=f(solvent)f(solution)=Kfm=72.08C72.0443C=72.59C1.070m=0.0357C=77.67023C.C=77.67C UATA TABLE 3 Molality of Naphthalene/Unknown Solution /5 points Experimental Molar Mass of Unknown /5 points Calculate the molar mass of your unknown in the space below. Use the chart to defermine the identity of the unknown based on the calculated experimental molar mass and record the name of the compound in Data Table 3. Introduction Freezing point depression is a colligative property. Colligative properties are those properties that depend on the amount of solute added to a solution. They are independent of the identity of the solute in an ideal solution where the interactions between solute and solvent molecules are similar to the intermolecular interactions of either pure solute or pure solvent. In addition to freezing point depression, other colligative properties include boiling point elevation, vapor pressure lowering, and osmotic pressure. Freezing point depression is based on a constant specific for the particular solvent and is proportional to the concentration of solute dissolved in the solvent. In this experiment, the solvent is naphthalene and the solute will initially be biphenyl, and then will be an unknown. Mothballs contain naphthalene, so you might recognize the odor. Theory In dilute solutions, the freezing point depression (Tf) is calculated using Equation 1: Tf=Tf(solvent)Tf(solution)=Kfm (Equation 1) In this experiment, Tf (solvent) is the point at which crystals first appear in pure naphthalene as determined graphically (see Figure 1). The literature value for T1 (naphthalene) is 80.2C. Any slight variations in your experimental results will be due to minor impurities present in the experimental grade naphthalene or to the thermometer. Next, Tf (solution) will be determined experimentally by freezing a mixture of naphthalene with a dissolved solute. It is the point at which crystals first appear in either the naphthalene/biphenyl or naphthalene/unknown mixtures (see Figure 2). Kf is the molal freezing point depression constant. This is a property of the solvent. Molality, m, is defined as moles solute (either biphenyl or an unknown) per kilograms of solvent (naphthalene), and is calculated by Equation 2: Molality=m=kilogramsofsolventmolesofsolute (Equation 2) The molecular formula for biphenyl is C12H10. In the first part of this experiment, Equation 1 will be arranged to determine the molal freezing point depression constant for naphthalene. In the second part of the experiment, Equation 1 will be rearranged to determine the molality of the naphthalene/unknown solution. Subsequently, the molar mass of the unknown will be determined. See Figure 1 for a cooling curve of pure naphthalene. You will note that the temperature decreases steadily until the freezing point. At this point, solid and liquid naphthalene are in equilibrium and the temperature is constant. When all of the naphthalene is frozen, the temperature drops. The line In a solute/solvent mixture, the solvent (naphthalene) generally freezes out of solution. The freezing is not constant as it was for pure naphthalene. Instead, the cooling curve of the mixture will show a gradual drop in the temperature during the time when freezing takes place. An additional feature of this graph may be the appearance of a region of supercooling where the mixture cools below the freezing point without the appearance of any crystals. The first crystal appears and the temperature begins to rise. The maximum temperature after the appearance of the first crystal is the freezing point of the mixture. This occurs at a lower temperature than that of the pure substance. See Figure 2 for a cooling curve of a naphthalene/biphenyl mixture. The line labeled Tf indicates an experimental freezing point of 72.5C. Figure 1: Cooling Curve Figure 2: Cooling Curve