Question: I need help please At what point does the line normal to the graph of y = 1 3:: + :2 at (1, 1) intersect
I need help please

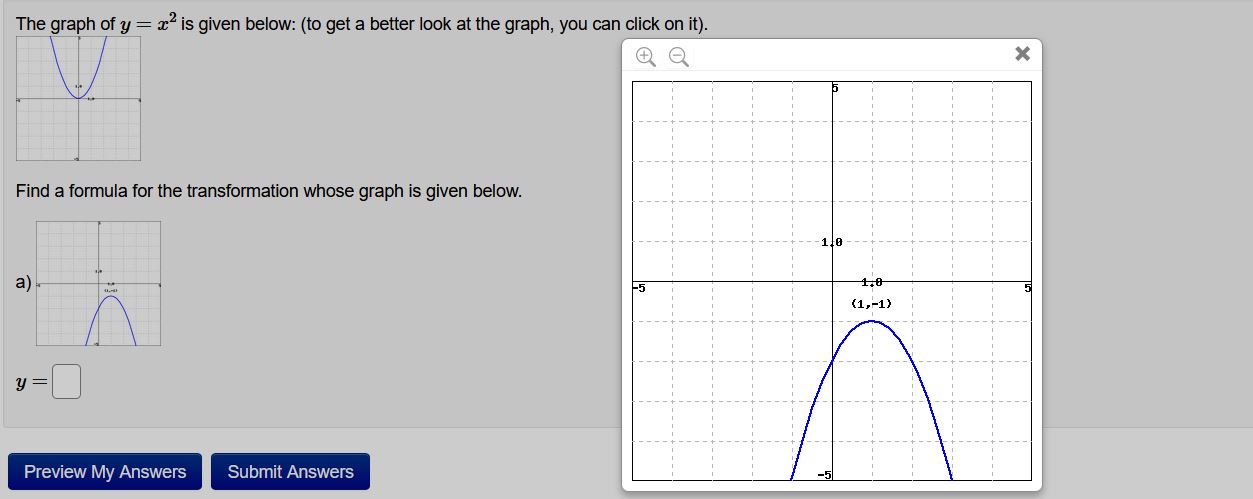



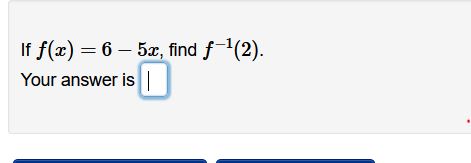
Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


