Question: I need help programing this in C please. computeDiffuse - Compute diffuse lighting term 1 Finclude In computer graphics one component of incorporating lights into
I need help programing this in C please.
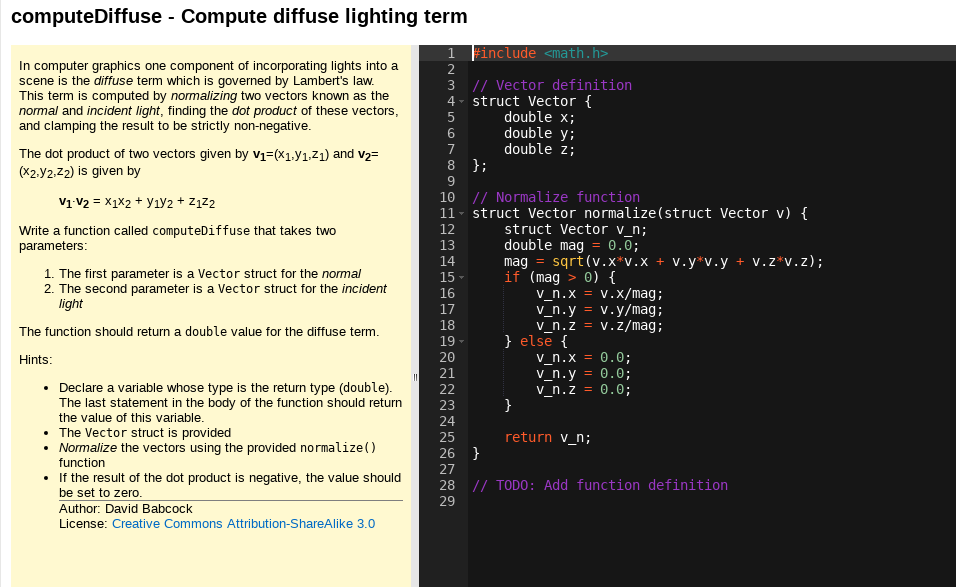
computeDiffuse - Compute diffuse lighting term 1 Finclude
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


