I need help with pre calc, thank you

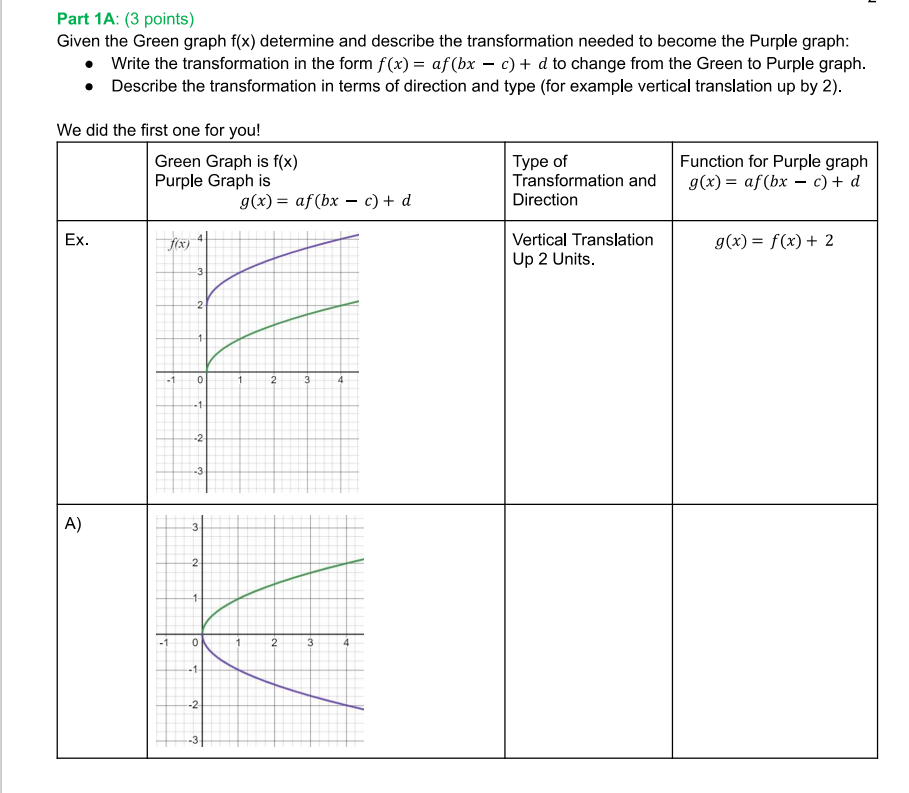
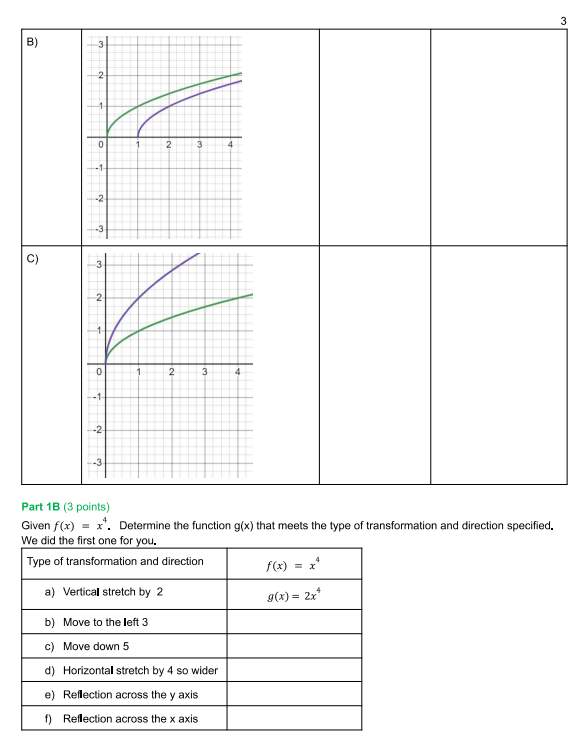
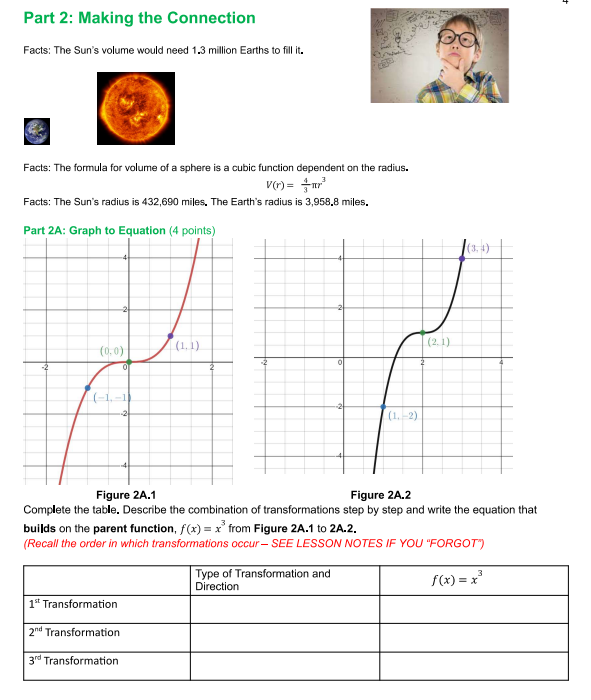
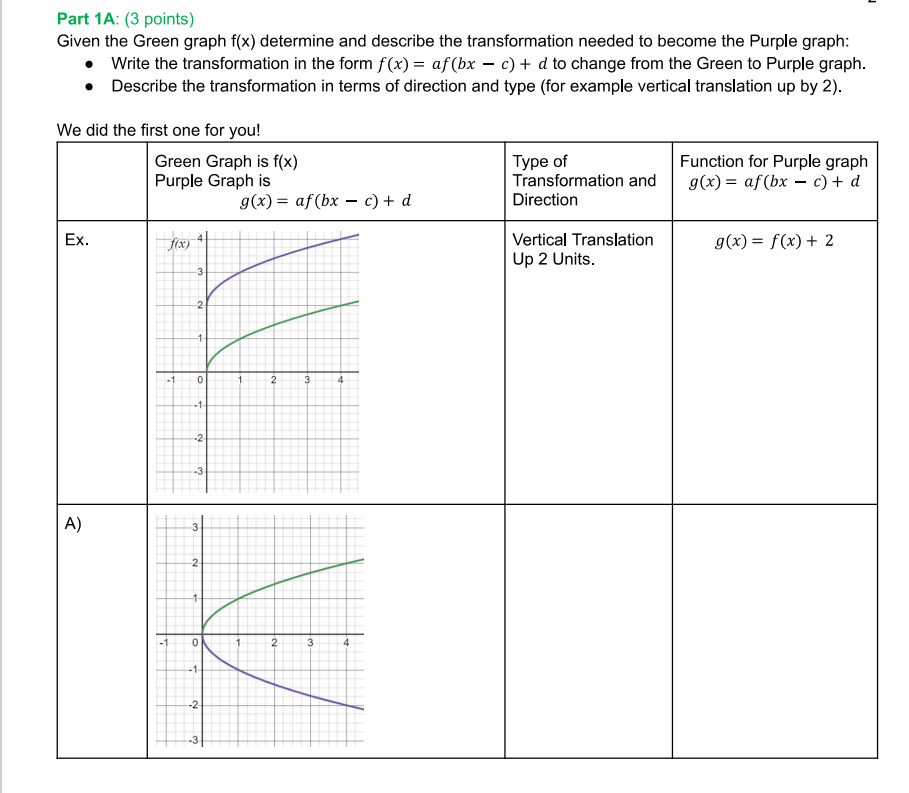
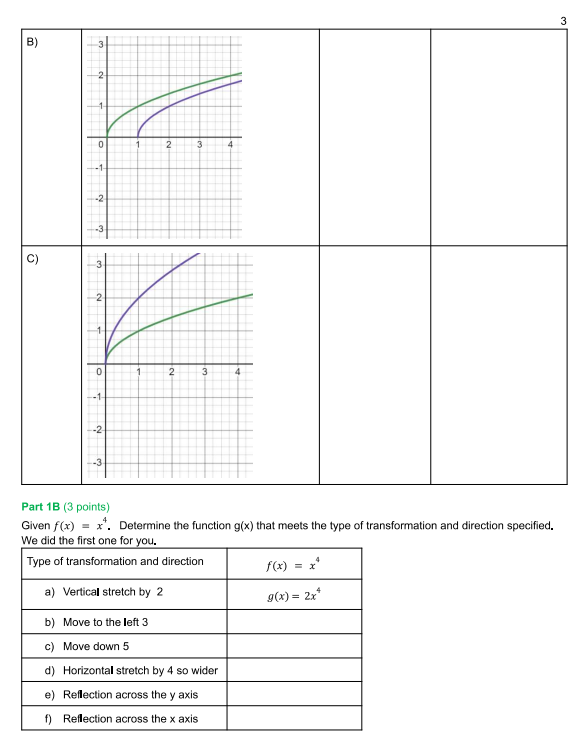
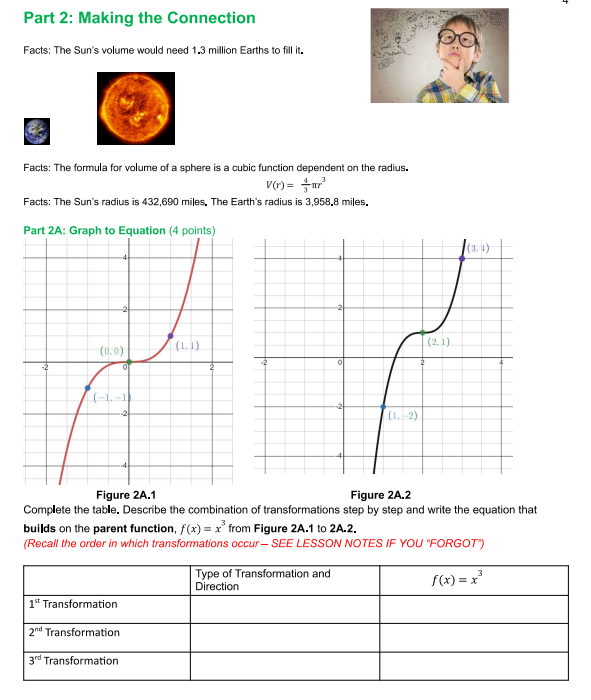
Name Date "Here Comes the Sun" - Portfolio Worksheet PreCalculus A - Unit 3 Lesson 8 Portfolio ** * * *DIRECTIONS: Before beginning, select FILE > MAKE A COPY of this Google Doc. Complete the portfolio and then convert the final submission to PDF (Download as a pdf or print as a pdf) and submit in Portfolio Drop Box in lesson 8.***** OPTIONAL EXTRA PRACTICE before beginning the portfolio. To help you complete the portfolio and better understand transformations and how they change the graph go through the following transformation examples in Desmos. . Vertical Shift f(x) = x2, f(x) - 2 and f(x) + 4 (Click for -> Example) Horizontal Shift f(x) = \\x, f(x-3), f(x+2), f(x+5), f(x-1) (Click for -> Example) . Reflection of x-axis h(x) = (x - 2)? + 1 and - h(x) (Click for -> Example) . Reflection of y-axis g(x) = /x - 2/ +1 and g(-x) (Click for -> Example) . Horizontal Stretch/Compression f(x) = x? -3, f( 2x) and f(2x) (Click for -> Example) . Vertical Stretch/Compression h(x) = x2 - 2, 2h(x) and 3h(x) (Click for -> Example) When you open up the Example links in Desmos, you can click on the "curvy" avatar to remove that particular graph. ~ " (x ) =x2 - 2 y = 2h(x) y = - h(x) My= 2(12 -2) 1/2Part 1A: [(3 points] Given the Green graph flx) determine and describe the transformation needed to become the Purple graph: o Write the transformation in the form f(x) = abx c) + d to change from the Green to Purple graph. - Describe the transformation in terms of direction and type (for example vertical translation up by 2). We did the rst one for you! Green Graph is f(x) Type of Purple Graph is Transformation and 9-0;}: abx c) + d Direction Function for Purple graph 30:) = abx c)+ d In; \" - Vertical Translation Up 2 Units. 307) = x) + 2 3 2 -2 -3 C) 1 0 2 3 --1- --2 1-3 Part 18 (3 points) Given f(x) = x'. Determine the function g(x) that meets the type of transformation and direction specified. We did the first one for you. Type of transformation and direction (x) = x a) Vertical stretch by 2 g(x) = 2x* b) Move to the left 3 c) Move down 5 d) Horizontal stretch by 4 so wider e) Reflection across the y axis () Reflection across the x axisPart 2: Making the Connection Facts: The Sun's volume would need 1.3 million Earths to fill it. Facts: The formula for volume of a sphere is a cubic function dependent on the radius. V(n) = +mr Facts: The Sun's radius is 432,690 miles. The Earth's radius is 3,958.8 miles. Part 2A: Graph to Equation (4 points) (3, 1) (2. 1) (0.0) (1, 1 ) (-1-1) -2 (1. 2) Figure 2A.1 Figure 2A.2 Complete the table. Describe the combination of transformations step by step and write the equation that builds on the parent function, f(x) = x from Figure 2A.1 to 2A.2. (Recall the order in which transformations occur- SEE LESSON NOTES IF YOU "FORGOT") Type of Transformation and Direction f (x) = x 1" Transformation 2"" Transformation 3" Transformation*Check your work by graphing the parent and your final equation using www.desmos,com to see if your points match up. You do not need to submit the graph. *** Part 28: The Connection (2 points) Now use the formula for volume of a sphere and complete the same 3 transformations used in Part 2A. This time apply the same transformation to the function for volume, V(r) = mr . V(r) = mr Type of Transformation and Direction - From Part 2A V(r) = -3 1" Transformation 2" Transformation 3" Transformation