I need help with Riemannian Geometry, please! I am trying to prove the following.

Let (M, g) be a Riemannian manifold with constant sectional curvature K. Let c : [0, L] M be a geodesic with arc-length parameterization. Let J be a Jacobi field along c, everywhere perpendicular to c' . Prove that the Jacobi equation, in this case, simplifies to J'' + KJ = 0.

Now, let w(s) be a parallel vector field along c, everywhere perpendicular to c 0 , and of constant norm equal to 1. Prove that

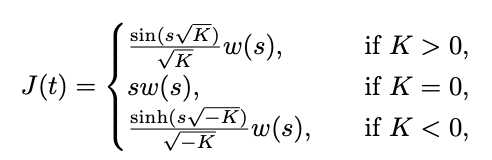if K J(t) = sin(sK) K Qw(s), sw(s), sinh(s-K)w(s), -K if K > 0, if K = 0, if K 0, if K = 0, if K