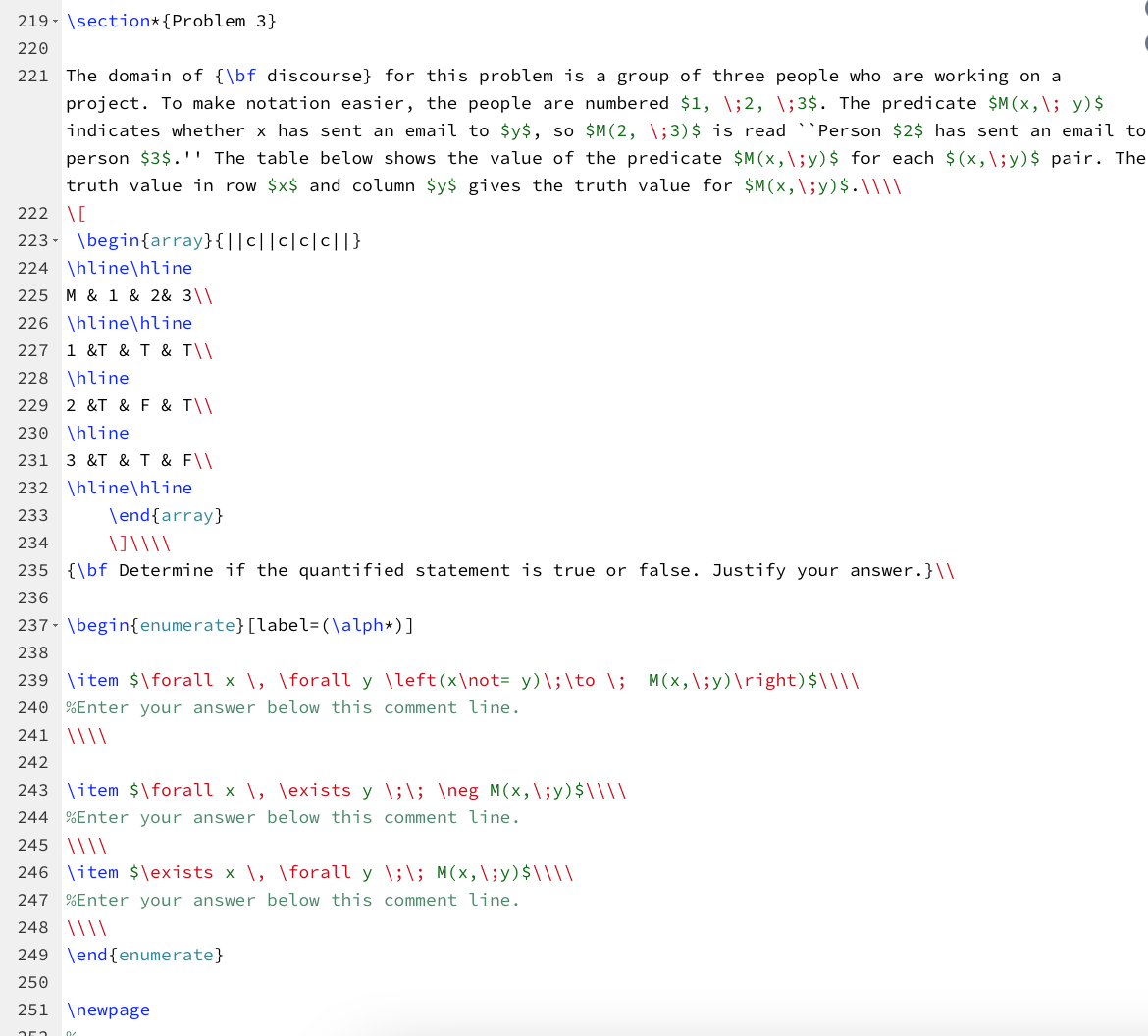
Question: I need help with these two problems in Discrete Math please and please answer these in LaTeX. 219 section* {Problem 3} 220 221 The domain
I need help with these two problems in Discrete Math please and please answer these in LaTeX.

Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


