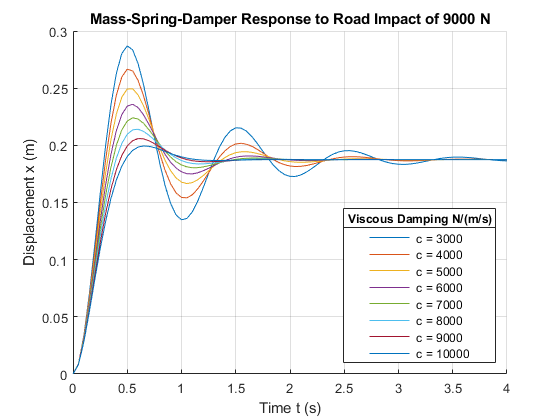
I need help with this in MATLAB. This is a continuation of the discussion during module week 7: In this case, the shock/suspension system of a car needs to be sized. Assume a car with a mass M = 1200 kg having a suspension system, where the overall spring constant k = 48000 N/m. The car hits a bump in the road, which is equivalent to a force of 9000N. Now, take eight different viscous shock absorbers c which ranges between 3000 N/(m/s) and 10000 N/(m/s). Plot the displacements as a function of time and discuss the results with your peers. Also, determine k and c such that the "Overshoot" is below 10% of its final value and the system has settled within 0.33 seconds.

This is what we used for equations last week. I guess possibly using this and updating the values and also add whatever the above question is asking. It may not even need these equations below, not sure. PLEASE HELP!

One can show that the motion can be described by the damping coefficient and the natural frequency , where and

With these equations last week in 7 we made this image.

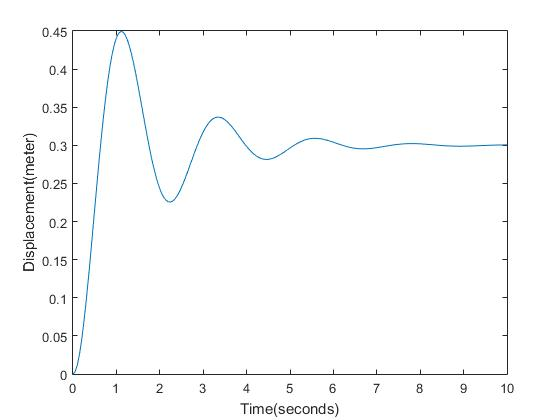
Here was the code for it.

k=100; m=12; c=15;f0=30; t=0:0.05:10;

w=sqrt(k/m);

ji=c/(2*sqrt(m*k));

x=(f0/k)*(1-exp(-ji*w*t).*((cos(sqrt(1-ji^2)*w*t))+(ji/sqrt(1-ji^2))*sin(sqrt(1-ji^2)*w*t)));

plot(t,x)

xlabel('Time(seconds)')

ylabel('Displacement(meter)')

Now for this week we have to build on this image and add in values from the paragrapgh at the top. Here is the new image on what people were getting. Do I need a loop to add each value to the plot?