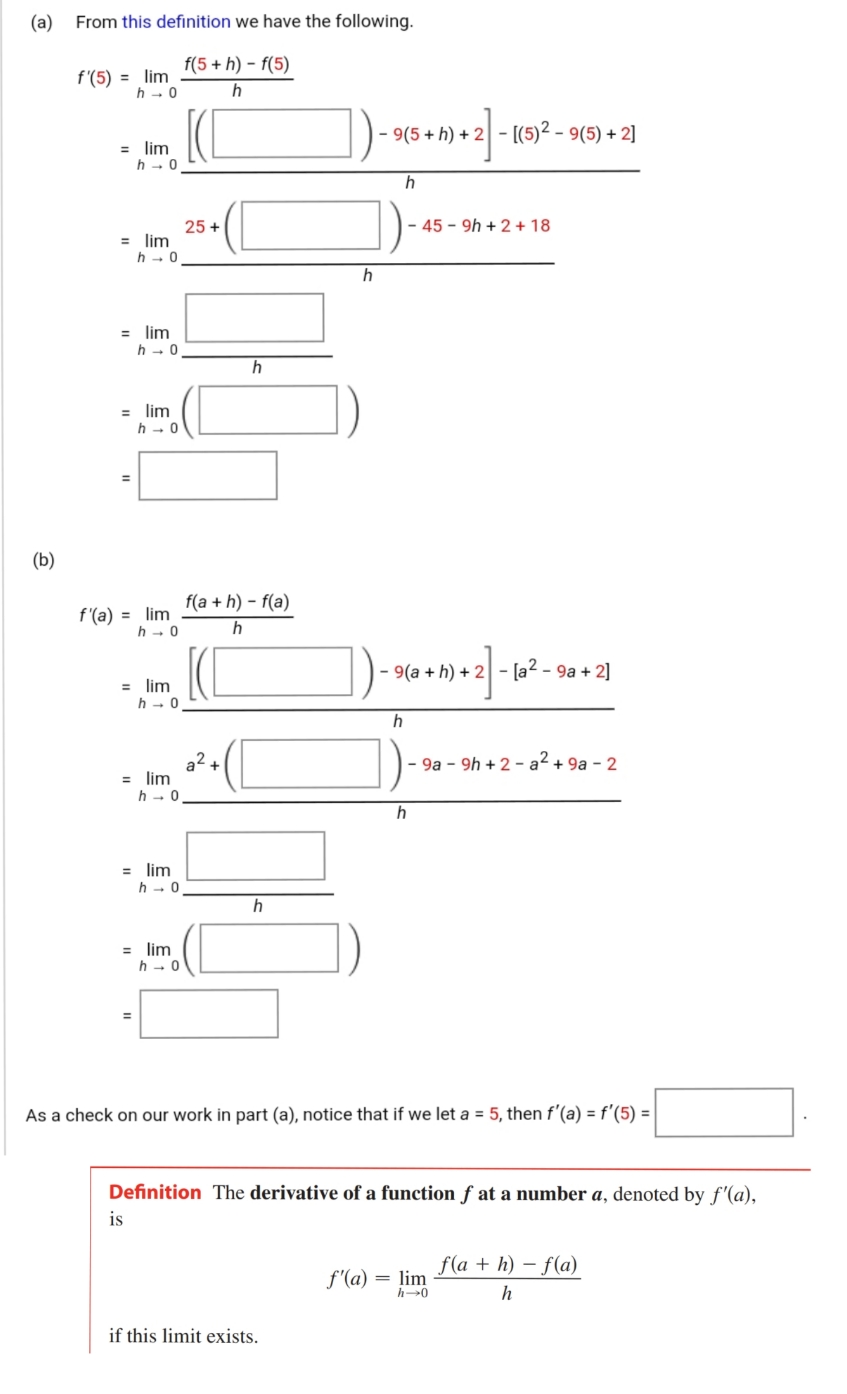
I need solve this question

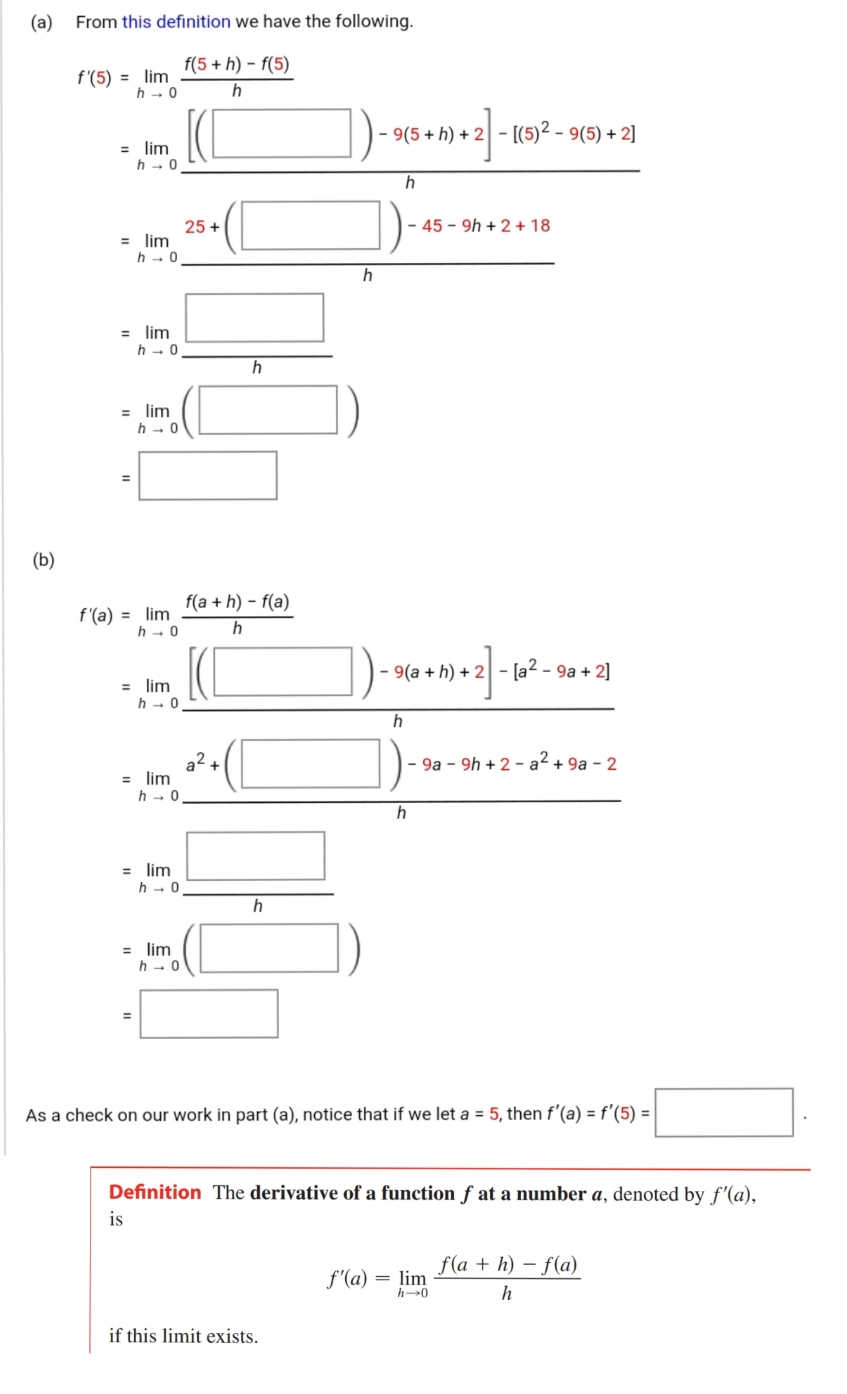
(a) From this definition we have the following. f'(5) = lim f(5 + h) - f(5) h - 0 h = lim 9 ( 5 + h ) + 2 - 1( 5 ) 2 - 9 ( 5 ) + 2 ] h - 0 h 25 + - 45 - 9h + 2 + 18 = lim h - 0 h = lim h - 0 h = lim h - 0 (b) f'(a) = lim f(a + h) - f(a) h - 0 h - 9(a + h) + 2 - [a2 - 9a + 2] = lim h - 0 h a-+ - 9a - 9h + 2 - a2 + 9a - 2 = lim h - 0 h = lim h - 0 h lim h - 0 As a check on our work in part (a), notice that if we let a = 5, then f'(a) = f'(5) = Definition The derivative of a function f at a number a, denoted by f'(a), is f'(a) = lim f(a + h) - f(a) h-0 h if this limit exists