I need this to be implemented in MATLAB. (Not Simulink)

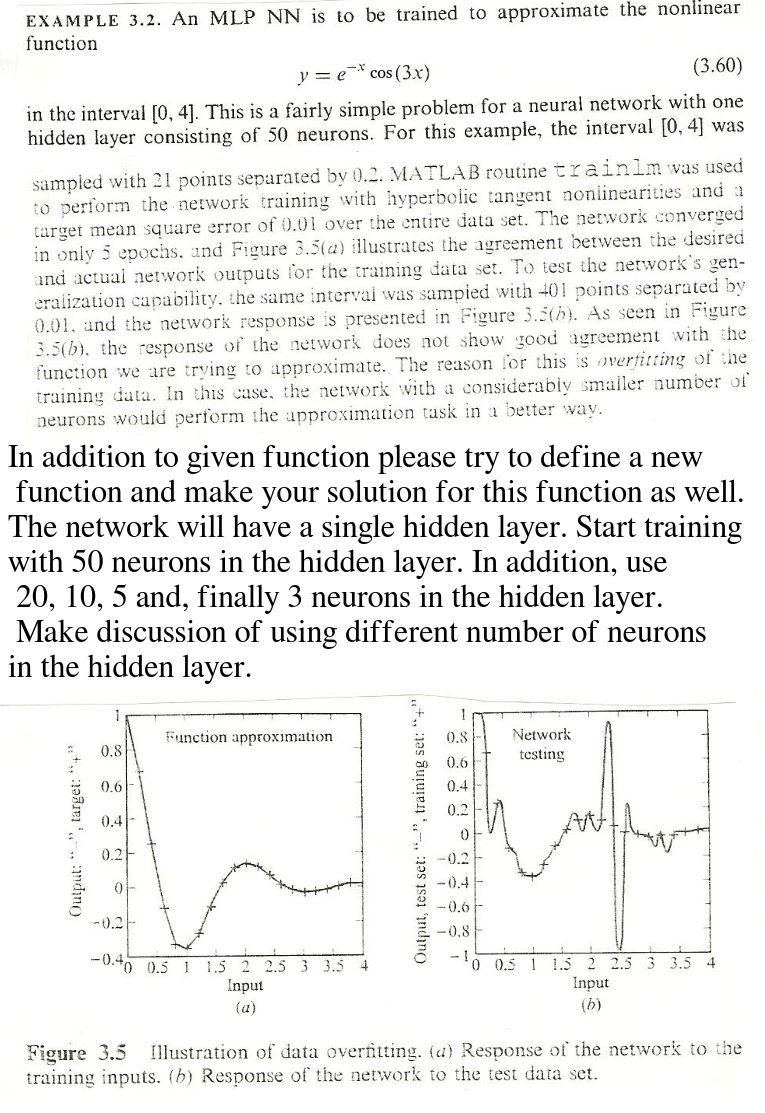
EXAMPLE 3.2. An MLP NN is to be trained to approximate the nonlinear function y = e-*cos (3x) (3.60) in the interval [0, 4]. This is a fairly simple problem for a neural network with one hidden layer consisting of 50 neurons. For this example, the interval [0, 4] was sampled with 21 points separated by 0.2. MATLAB routine trainlm was used to perform the network training with hyperbolic tangent nonlinearities and a target mean square error of 0.01 over the entire data set. The network converged in only 5 epochs, and Figure 3.51a) illustrates the agreement between the desired and actual network outputs for the training data set. To test the network's gen- eralization capability, the same interval was sampied with 401 points separated by 0.01. and the network response is presented in Figure 3.5(b). As seen in Figure 3.5(b), the response of the network does not show good agreement with the function we are trying to approximate. The reason for this is overfirting of the training data. In this case, the network with a considerably smaller number of neurons would perform the approximation task in a better way. In addition to given function please try to define a new function and make your solution for this function as well. The network will have a single hidden layer. Start training with 50 neurons in the hidden layer. In addition, use 20, 10, 5 and, finally 3 neurons in the hidden layer. Make discussion of using different number of neurons in the hidden layer. 1 1 0.8 Function approximation 0.8 Network testing 0.6 0.6 0.4 0.2 0.4 0.2 o 0 -0.2 -0.4 -0.6 -0.8 -0.2 -0.40 0.5 1 1.5 2 2.5 3 3.5 Input (a) 0 0.5 1 1.5 2 2.5 3 3.5 4 Input (b) Figure 3.5 Illustration of data overfitting. (a) Response of the network to the training inputs. (b) Response of the network to the test data set. EXAMPLE 3.2. An MLP NN is to be trained to approximate the nonlinear function y = e-*cos (3x) (3.60) in the interval [0, 4]. This is a fairly simple problem for a neural network with one hidden layer consisting of 50 neurons. For this example, the interval [0, 4] was sampled with 21 points separated by 0.2. MATLAB routine trainlm was used to perform the network training with hyperbolic tangent nonlinearities and a target mean square error of 0.01 over the entire data set. The network converged in only 5 epochs, and Figure 3.51a) illustrates the agreement between the desired and actual network outputs for the training data set. To test the network's gen- eralization capability, the same interval was sampied with 401 points separated by 0.01. and the network response is presented in Figure 3.5(b). As seen in Figure 3.5(b), the response of the network does not show good agreement with the function we are trying to approximate. The reason for this is overfirting of the training data. In this case, the network with a considerably smaller number of neurons would perform the approximation task in a better way. In addition to given function please try to define a new function and make your solution for this function as well. The network will have a single hidden layer. Start training with 50 neurons in the hidden layer. In addition, use 20, 10, 5 and, finally 3 neurons in the hidden layer. Make discussion of using different number of neurons in the hidden layer. 1 1 0.8 Function approximation 0.8 Network testing 0.6 0.6 0.4 0.2 0.4 0.2 o 0 -0.2 -0.4 -0.6 -0.8 -0.2 -0.40 0.5 1 1.5 2 2.5 3 3.5 Input (a) 0 0.5 1 1.5 2 2.5 3 3.5 4 Input (b) Figure 3.5 Illustration of data overfitting. (a) Response of the network to the training inputs. (b) Response of the network to the test data set