I never do not know how to access this problem by invariant. Could you show me how to solve this problem?

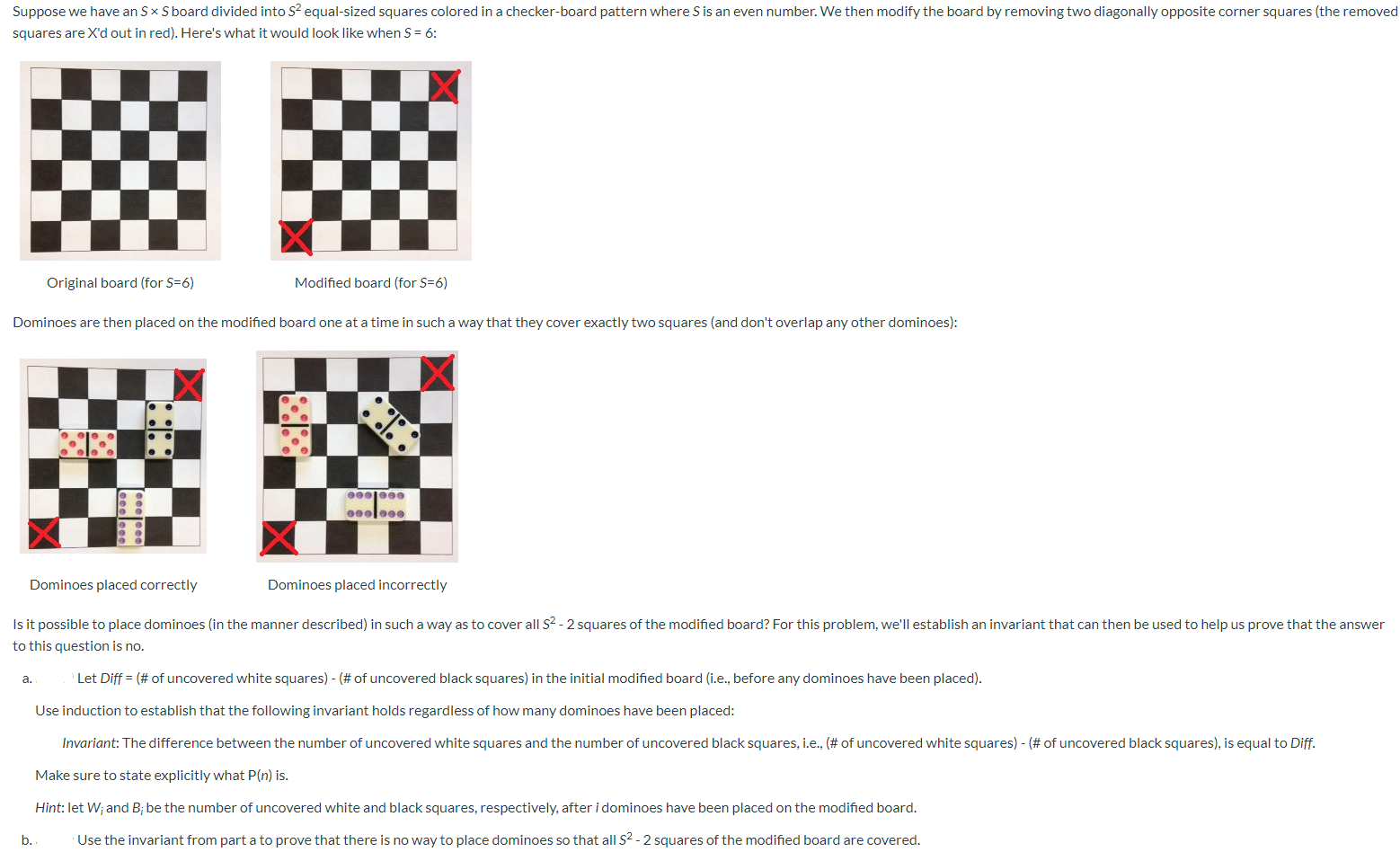
Suppose we have an S x S board divided into S equal-sized squares colored in a checker-board pattern where S is an even number. We then modify the board by removing two diagonally opposite corner squares (the removed squares are X'd out in red). Here's what it would look like when S = 6: Original board (for 5=6) Modified board (for S=6) Dominoes are then placed on the modified board one at a time in such a way that they cover exactly two squares (and don't overlap any other dominoes): .. ..0. Dominoes placed correctly Dominoes placed incorrectly Is it possible to place dominoes (in the manner described) in such a way as to cover all S" - 2 squares of the modified board? For this problem, we'll establish an invariant that can then be used to help us prove that the answer to this question is no. a. Let Diff = (# of uncovered white squares) - (# of uncovered black squares) in the initial modified board (i.e., before any dominoes have been placed). Use induction to establish that the following invariant holds regardless of how many dominoes have been placed: Invariant: The difference between the number of uncovered white squares and the number of uncovered black squares, i.e., (# of uncovered white squares) - (# of uncovered black squares), is equal to Diff. Make sure to state explicitly what P(n) is. Hint: let W; and B; be the number of uncovered white and black squares, respectively, after i dominoes have been placed on the modified board. b. . Use the invariant from part a to prove that there is no way to place dominoes so that all $2 - 2 squares of the modified board are covered