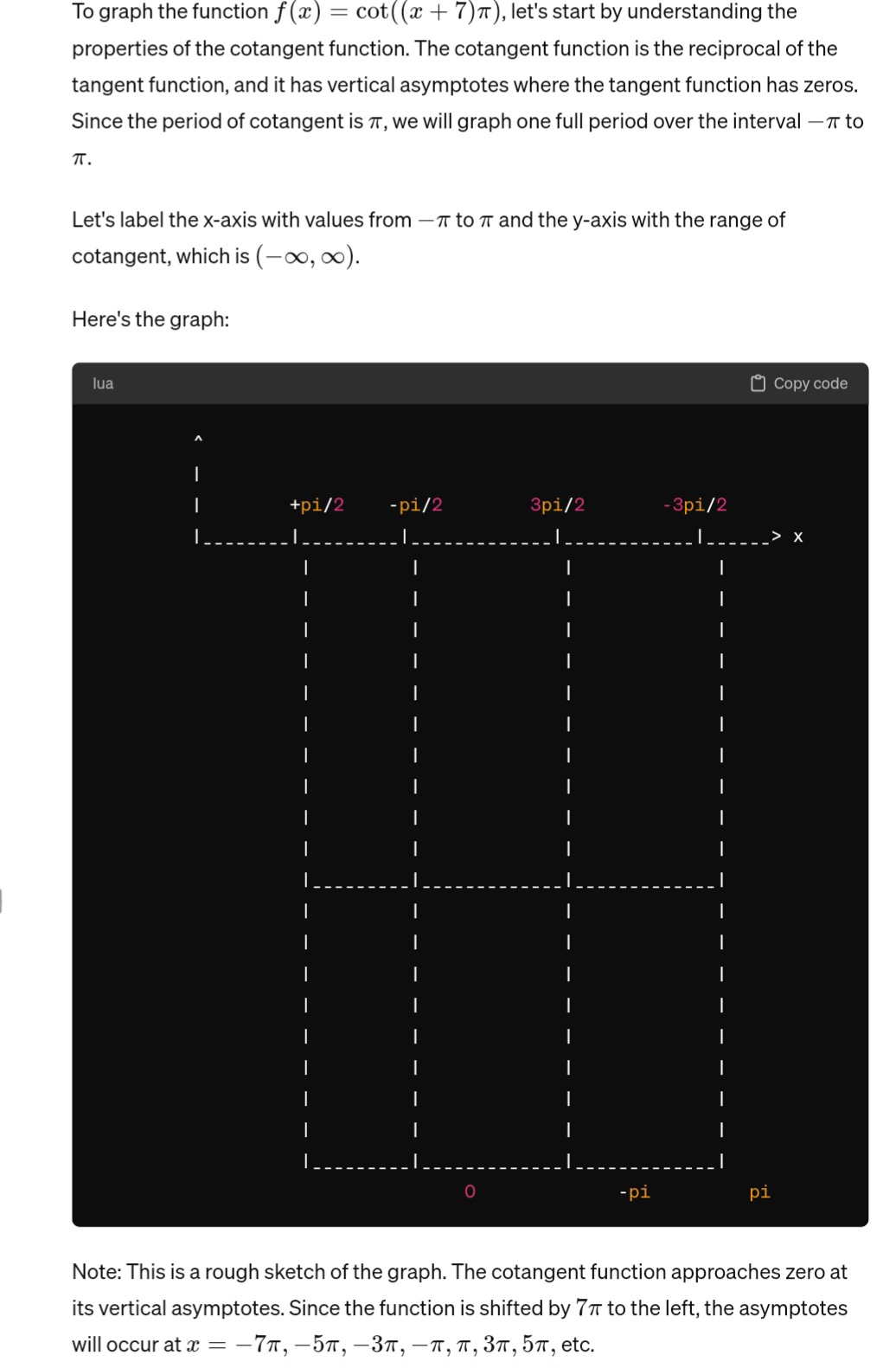
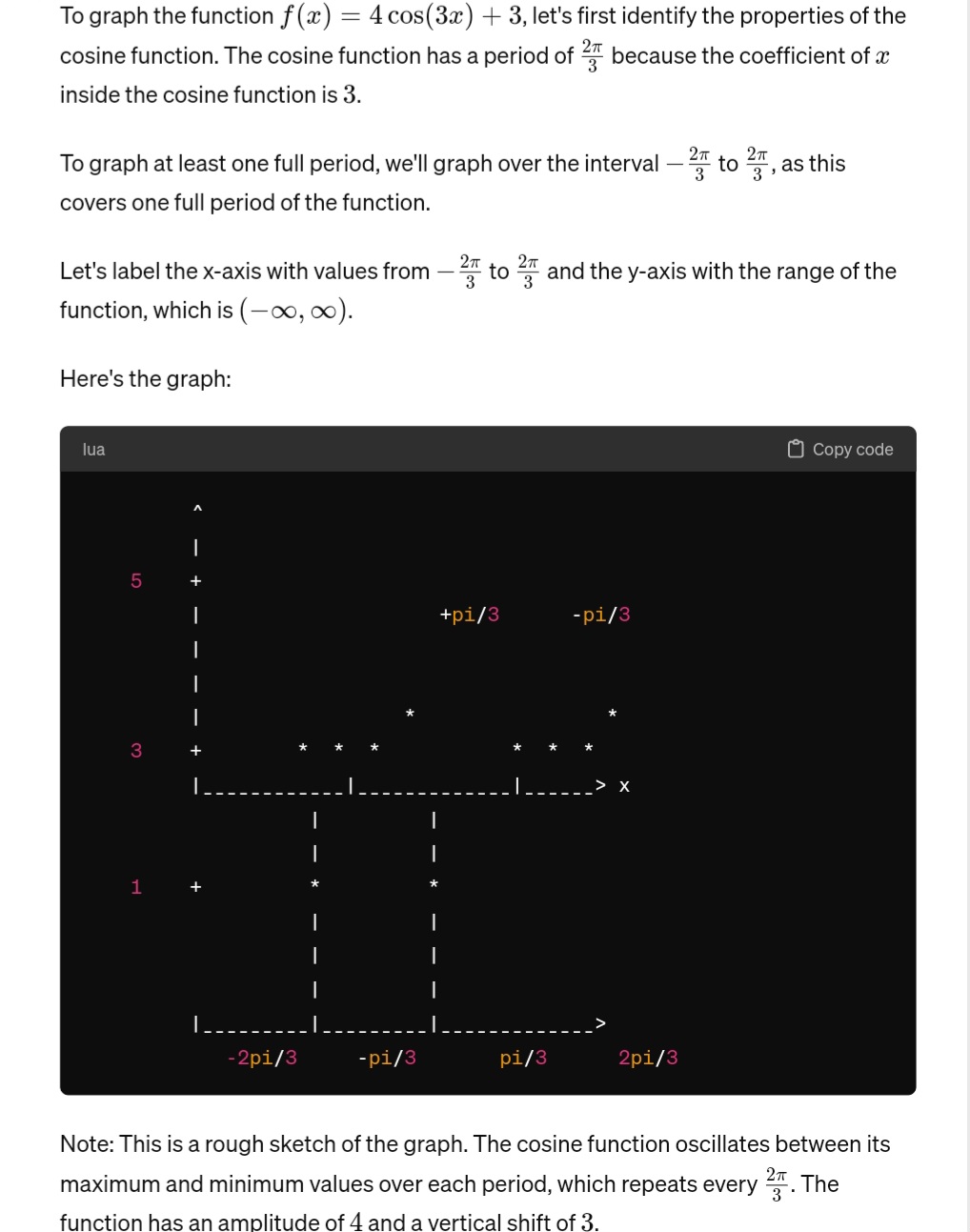
i/ T 1. Graph the function 7 x) =cot| _'|;+E J Be sure to clearly label the axes and graph at least one full period L of the function. Answer: 2 T 2. Graph the function f(x)= 4cos| E.'l;+E JB. Be sure to clearly label the axes and graph at least one full Y period of the function. Answer: (Score for Question J._ _ Of 4 points) 3. The range of a cosecant function is (-00, -9 \\|5,00). The equations of two consecutive asymptotes of the function are x = 0 and x=2x . The function is not a reflection over the x-axis. What is the equation of this cosecant function? Answer.To graph the function f(x) = cot((x + 7)), let's start by understanding the properties of the cotangent function. The cotangent function is the reciprocal of the tangent function, and it has vertical asymptotes where the tangent function has zeros. Since the period of cotangent is 7, we will graph one full period over the interval to . Let's label the x-axis with values from 7 to 7m and the y-axis with the range of cotangent, which is (00, 00). Here's the graph: [j Copy code Note: This is a rough sketch of the graph. The cotangent function approaches zero at its vertical asymptotes. Since the function is shifted by 77 to the left, the asymptotes willoccuratx = 7n, dm, 3m, m, m, 3w, O, etc. To graph the function f(:r) =4 (:05(3:1:) + 3, let's first identify the properties of the cosine function. The cosine function has a period of 2% because the coefficient of & inside the cosine function is 3. To graph at least one full period, we'll graph over the interval 277 to %T as this covers one full period of the function. Let's label the x-axis with values from 2{ to 2; and the y-axis with the range of the function, which is (o0, 00). Here's the graph: () Copy code Note: This is a rough sketch of the graph. The cosine function oscillates between its maximum and minimum values over each period, which repeats every %' The function has an amplitude of 4 and a vertical shift of 3. Given the information provided, we know that the cosecant function has asymptotes atz = 0and x = 27. This implies that the period of the function is 27, since cosecant functions repeat at intervals of their period. Additionally, we know that the range of the cosecant function is (oo, 9] U [5, 00). Since cosecant is the reciprocal of sine, we can deduce that the sine function has a range of (o0, 5] U [5, 00). The sine function has its maximum value of 1 atx = %, and its minimum value of 1 atxr = % Given that the period is 27, we need to scale this to fit our period. So, the equation of the sine function with the given range and period can be written as: f(z) = Asin (%';:1:) + B Where A is the amplitude and B is the vertical shift. To fit the given range, A should be chosen such that the amplitude is % and the vertical shift should be g- to ensure that the range is shifted to (9, 5). Therefore, the equation of the cosecant function is: 2 9 f(z) = cse (57x) 3 This function will have asymptotes at z = 0 and x = 27, with the given range. M O 6