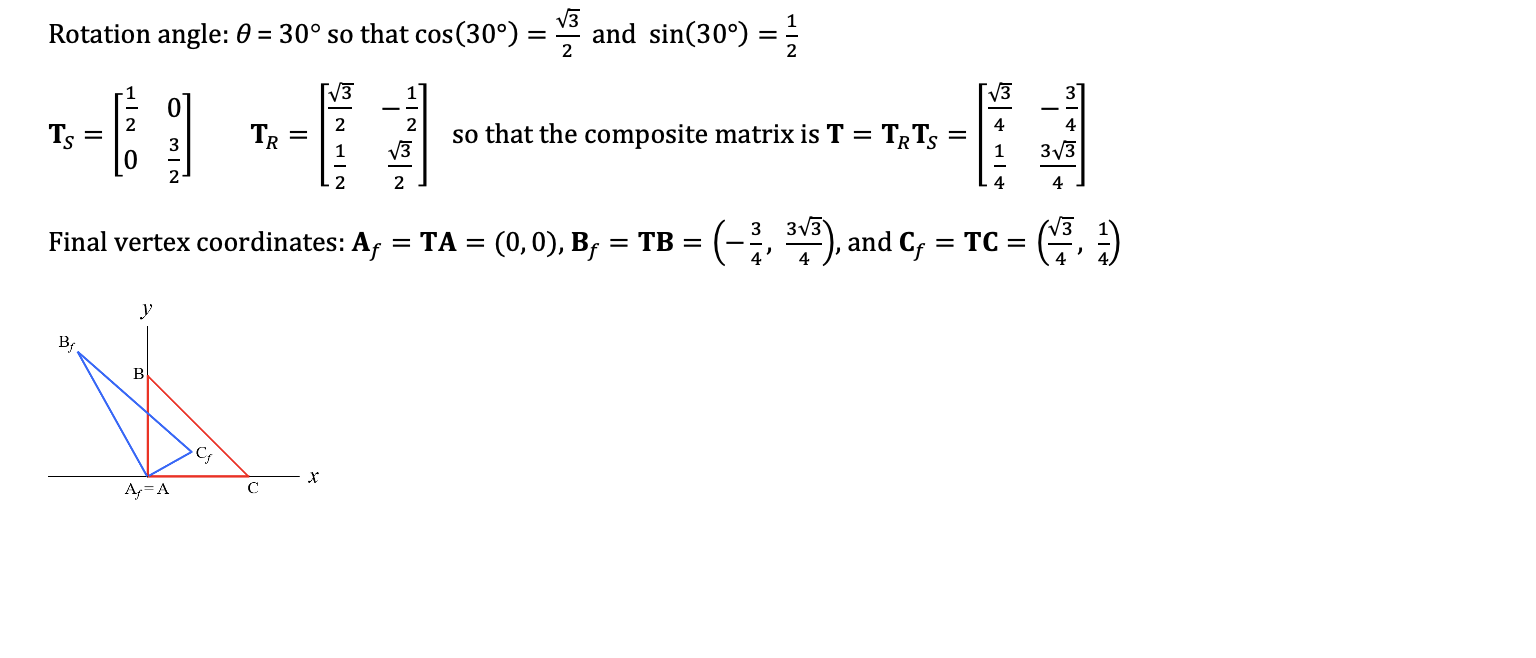I will rate.Thank you

In computer graphics, it is a common task to scale or rotate shapes on the screen. The coordinates of each defined point P = (x,y) on the shape are multiplied by a 2x2 transformation matrix T to get the final coordinates P': P = TP + m]=7[3] =T Scaling: Ts = LE ) These are some basic 2-D transformation matrices (there are more, but these are sufficient for our purposes): Sx 0 = where Sxand Sy are the scaling factors in the x-axis and y-axis directions, respectively. These are used to either expand or contract the shape's size in a given direction. [cos(O) -sine Rotation (ccw): TR (sin(e) cos(0) , where is the counterclockwise rotation angle w.r.t. the x-axis. This allows you to rotate the shape. ] You can apply transformations one after another by creating a single composite transformation matrix: Composite: T = T3T2T1, where each Tk is a transformation matrix. They are applied from right to left. Example: The 2-D triangle shown below is to be scaled by 0.5 in x and 1.5 in y and then rotated 30 counterclockwise. 3 B (0,1) (0,0) A (1.0) What is the composite matrix and the final coordinates of each vertex? What does the final result look like on a graph? Solution: = Original vertex coordinates: A = (0,0), B = (0,1), C = (1,0) Scaling factors: Sx = { and Sy = Rotation angle: 6 = 30 so that cos(30) = { and sin(30) = { = V3 Rotation angle: 0 = 30 so that cos(30) and sin(30) = 2 V3 3 2 TS TR 2 V3 so that the composite matrix is T = TRTs = = All 4 373 2 2 V3 Final vertex coordinates: Af = TA = (0,0), Bf = TB = = 3 3V3 4' and G. = TC= (3.3) a 4 y BA B C . A,=A C In computer graphics, it is a common task to scale or rotate shapes on the screen. The coordinates of each defined point P = (x,y) on the shape are multiplied by a 2x2 transformation matrix T to get the final coordinates P': P = TP + m]=7[3] =T Scaling: Ts = LE ) These are some basic 2-D transformation matrices (there are more, but these are sufficient for our purposes): Sx 0 = where Sxand Sy are the scaling factors in the x-axis and y-axis directions, respectively. These are used to either expand or contract the shape's size in a given direction. [cos(O) -sine Rotation (ccw): TR (sin(e) cos(0) , where is the counterclockwise rotation angle w.r.t. the x-axis. This allows you to rotate the shape. ] You can apply transformations one after another by creating a single composite transformation matrix: Composite: T = T3T2T1, where each Tk is a transformation matrix. They are applied from right to left. Example: The 2-D triangle shown below is to be scaled by 0.5 in x and 1.5 in y and then rotated 30 counterclockwise. 3 B (0,1) (0,0) A (1.0) What is the composite matrix and the final coordinates of each vertex? What does the final result look like on a graph? Solution: = Original vertex coordinates: A = (0,0), B = (0,1), C = (1,0) Scaling factors: Sx = { and Sy = Rotation angle: 6 = 30 so that cos(30) = { and sin(30) = { = V3 Rotation angle: 0 = 30 so that cos(30) and sin(30) = 2 V3 3 2 TS TR 2 V3 so that the composite matrix is T = TRTs = = All 4 373 2 2 V3 Final vertex coordinates: Af = TA = (0,0), Bf = TB = = 3 3V3 4' and G. = TC= (3.3) a 4 y BA B C . A,=A C