i would like to know if my answer are correct on relation subject

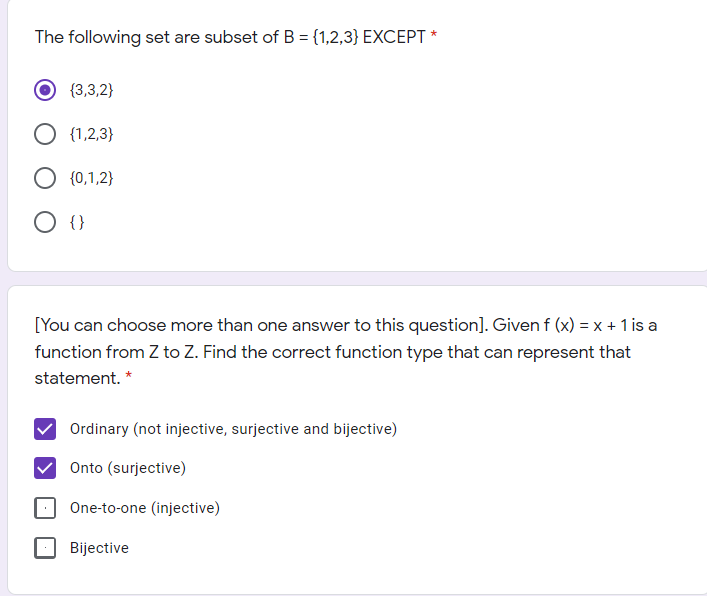
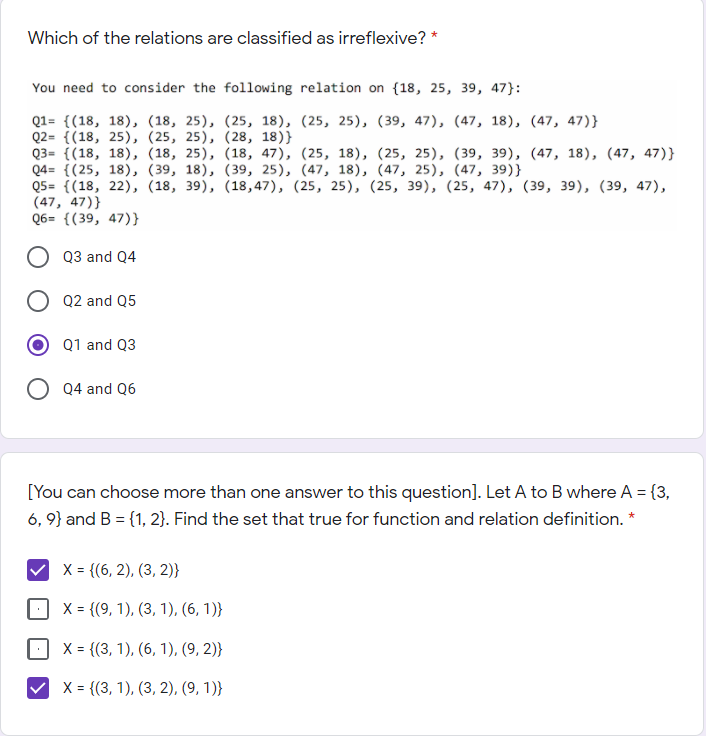
The following set are subset of B = {1,2,3} EXCEPT* (3,3,2) O {1,2,3) O {0,1,2) OO [You can choose more than one answer to this question]. Given f (x) = x + 1 is a function from Z to Z. Find the correct function type that can represent that statement. * Ordinary (not injective, surjective and bijective) Onto (surjective) One-to-one (injective) Bijective Which of the relations are classified as irreflexive? * You need to consider the following relation on {18, 25, 39, 47}: Q1= {(18, 18), (18, 25), (25, 18), (25, 25), (39, 47), (47, 18), (47, 47)} Q2= {(18, 25), (25, 25), (28, 18)} Q3= {(18, 18), (18, 25), (18, 47), (25, 18), (25, 25), (39, 39), (47, 18), (47, 47) } Q4= {(25, 18), (39, 18), (39, 25), (47, 18), (47, 25), (47, 39)} Q5= {(18, 22), (18, 39), (18,47), (25, 25), (25, 39), (25, 47), (39, 39), (39, 47), (47, 47)} Q6= {(39, 47)} 23 and 24 Q2 and 25 Q1 and 23 Q4 and 26 [You can choose more than one answer to this question). Let A to B where A = {3, 6,9} and B = {1, 2}. Find the set that true for function and relation definition. * X = {(6,2), (3, 2)} X = {(9, 1), (3, 1), (6, 1)} X = {(3, 1), (6, 1), (9, 2)} = X = {(3, 1), (3, 2), (9, 1)) [You can choose more than one answer to this question]. Given set X and Y where X = {1, 2, 3, 4} to Y = {A, B, C, D}. Find a function that can be constructed from a given statement. * f(x) = {(1,A),(2,A),(3,B),(3,C),(4,D)} f(x) = {(1,A),(2,B),(3, D), (4, C)} f(x) = {(1,A),(2,A),(3,B),(4, D)} f(x) = {(1,A),(2,A),(2,C),(3,B),(4, D)} [You can choose more than one answer to this question). Let f: RR. Determine the type of function for f(x) = 6x-9* Onto (surjective) Ordinary (not injective, surjective and bijective) Bijective One-to-one (injective) Given a relation Pis defined on a set of Q, where: P = {(3, 4), (4,5), (5, 4), (6,3)} and Q = {3, 4, 5, 6}. Which is the following is the symmetric closure of P?* PU{ (4,3), (6,3)} PU{(4,5), (1,4)} O QU{(4, 5), (1,4) } { O PU{ (4,3), (3,6) }