I would like to summarize this section, with an example for clarification, please

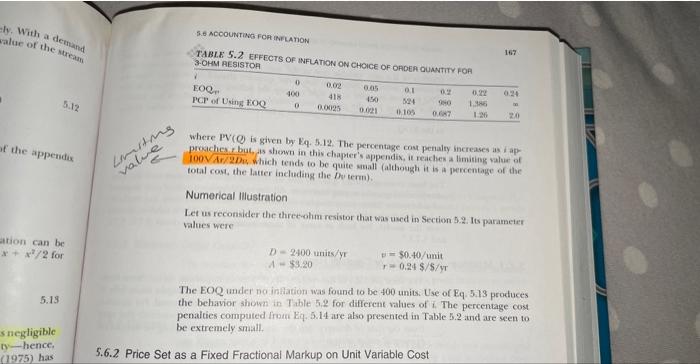
Que of the aswumptions in the derivaron of the ecemotmic opver quantit wan itat becen confectesed wath Guctuating inflation nates that ofien tave bect far from 5.6.1 Price Established independent of Ordering Policy Becaune the price is establabed independent af the ordering pohcy (pertapa priming is set by market farces exiermall te the company under consilleration). We can reatrict our athention. as earlief, to the mituitnization of costs. Howeres, becaise cossa aft charging with time, we canivot compase conta over a typucall year, an in Fection 5 s. Insitad, we tesort to a common bool of imeatahent analysit., hamely, that bie of the Soppose that the continuous discount fale is dracited by r2 that in, a coat ef if at time 4 has a pecsent value of a . Dote that o is the constant 2,71829.+1. denote the centituous inflasion tate by d. Taus, if A ard q are the cont factorn at rate of D and an otder of siae Qreceived at time 0 , the peesent value of the ataream of costs is giveat be? For a mininuam, we set dPVTO.VAQ = 0. Aa alwom in Section 2 od the appendix ol tain chapter, thee revalt in 5.6.1 Price Established Independent of Ordering Policy Because the price is catablithed independent of the ordering policy (perhaps priking is set by market forcesexiernal so the company under consideration), we can rezerict our attention, as earlier, to the minimiradion of costs. However, because conts are changing with time, we cannot compare conts over a lastead, we tesont to a common aool of invertenent analyria, namely, the use of the present value (PV) of the streas of fature costs. Seppose that the continoow discount nate is deeoted by , that is, a cost of cat time t has a present value of a "s, Note that t is the conseant 2.71829.. . We denote the continuous inflution rase by i . Thush if A and v are the cont factors at that inflation a at a mace iesonsille lewel. time rero, then their taloes at time tare A and tr, rerpectively. With a demand tate of D and an otder of siae Qrecenved as time 0 , the peesent valae of the stream of cosis is given tn ? For a minimun, we set dPV(Q)/dQ = 0. As thown in Soction if of the appendix of this chapier, the reault is ros=1+(vA+Q)(Dri) For (ri)Q/D, 1 , which in a reamonable asmamption, this equation can be simplified further by apgroximating the coponential term (e2=1+x+x2/2 for s of 1). Again, in the appendix we obain the fellonieg rende: Qr=1(rt)20D=50Q1i/x1 that is, the EOQ multiplied by acorrection factoe. Note that, when there is negligible inflation (i=0), this is nothing more than the econetnic oeder quantity-bence, our justification for using the nymbeil + for the discount rate. Buracots (1975) has developed a somewhat more eract deciaion rele, for which the reault of Eq. 5.13 is usually a good appronimation. Sece also Jese (Jr.). Mitra and Cax (1983). Kanet and Males (1985) and Mehra. Mgraal abd Raygopalan (1991) who incluale a verim for storage costs exclasive of the opportuniry cont of capital. Sarker and Pan (1994) determine the optimal order quatity and atiowable thortages in a tinise feplen- In an indlationary environment when price a set independent of ordering pobscy, the profis per unit increases with time lience the Lat replenishument thus, intuitively, the replenialament quantity abould be larger than under no inflation. Equation 5.13 indicates this type of behanior. The cort penalny acsociated with uting the FOQ (dhat ipnores inflation) ean be found froen PCF=FV(Qn)F(EOQ)PV(Q)1005.14 The derwanino wars the fact thal 1+a+an==1a10d