I wrote a program, but the middle algorithm and the correct result are not the same, can you help to see the arithmetic formula where to correct it? Thank you. The correct result is printed on paper. Programing C

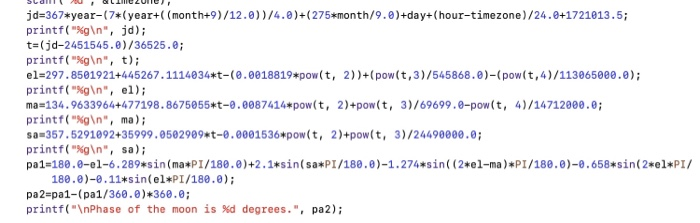
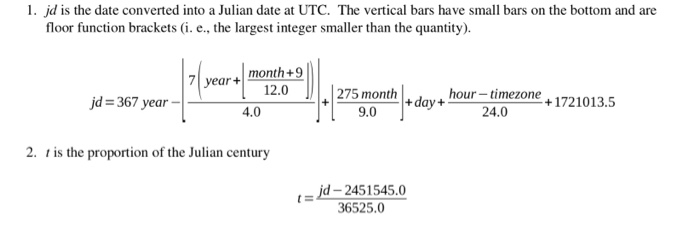
Enter year: 2016 Enter month (1-12): 7 Enter day: 4 Enter hour in 24-hour format: 6 Enter timezone: -5 2.45757e+06 0.165052 73790 Phase of the moon is e degrees. jd 367*year(7*(year+((month+9)/12.0))/4.0)+(275*month/9.8)+day+(hour-timezone)/24.0+1721013.5 printf("%g ", jd); t-(jd-2451545.0)/36525.e; printf("%g ", t); e1-297.8501921+4452671114834*t-(8.0018819*pow(t, 2)1+(pow(t,3)/545868 . )-( pow(t,4)/113965000 ,0); printf("g ", el); ma-134.9633964+477198.8675055*t-0.0087414*pow(t, 2)+pow(t, 3)/69699.0-pow(t, 4)/14712000.0; printf("%g ", ma); a 357.5291092+35999.0582909 t-0.8001536 pow(t, 2)+pow(t, 3)/24490000.0 printf("gIn", sa) 1-188.0-e1-6. 289#5 in (ma*PI/180.0)+2.1+sin( sa*PI/188. )-1.274*sin( (2#81-ma)*PI/186. )-8.658*sin( 2*el+PI/ 180.0)-0.11sin(el PI/180.0); pa2-pa1-( pa1/368 .0)*368 , 0; printf(" Phase of the moon is %d degrees.", pa2); 1. jd is the date converted into a Julian date at UTC. The vertical bars have small bars on the bottom and are floor function brackets (i. e., the largest integer smaller than the quantity). 7year+month+9 jd=367 year _| 12.0-1275 month hour- timezone+1721013.5 +day+ 9.0 24.0 2. t is the proportion of the Julian century t=jd-24515450 36525.0 3. el is the moon's mean elongation in degrees, the angle between the sun and the moon with Earth as the reference point el = 297.850 1921 + 445267.1 1 1 4034 t-0.00 1 88 19 t 545868.0 113065000.0 4. ma is the moon's mean anomaly in degrees, the angular distance from the pericenter of the moon's elliptical orbit which a fictitious moon would have if it moved in a circular orbit, with constant speed, in the same orbital period as the actual moon in its elliptical orbit ma 134.9633964+477198.8675055 0.0087414t+o 69699.0 14712000.0 5. sa is the sun's mean anomaly in degrees sa = 357.5291 092 + 35999.0502909 0.000 1 536t4 24490000.0 6. pa is the phase angle of the moon in degrees. However, the trigonometric library functions in C require their arguments to be in radians (rather than degrees). The formula for converting degrees to radians is radians- degrees180 and is used to convert the various angles into radians as follows pa = 180.0-el-6.289 sin l ma l al+2. 1 sinlsa 1800-1.274 sin|Zel-rna )18 al 0.658sin 2el 0.2 sin 2 ma -0, 1 1 sinel