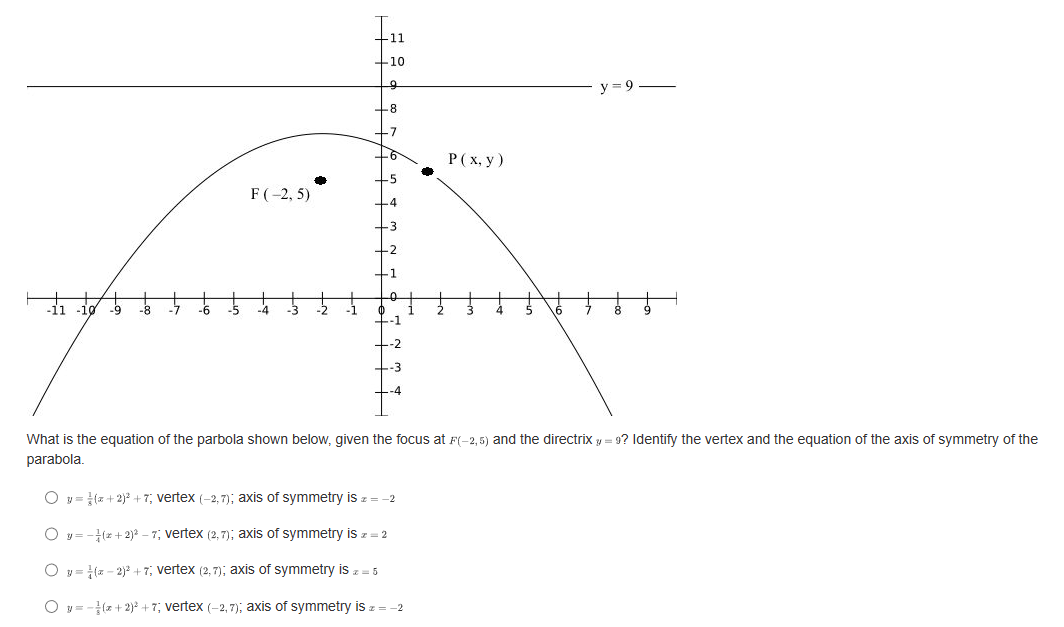
Question: If a parabola's focus is at (3,8) and directrix is at y = 2, what is the vertex form of the equation representing this parabola?

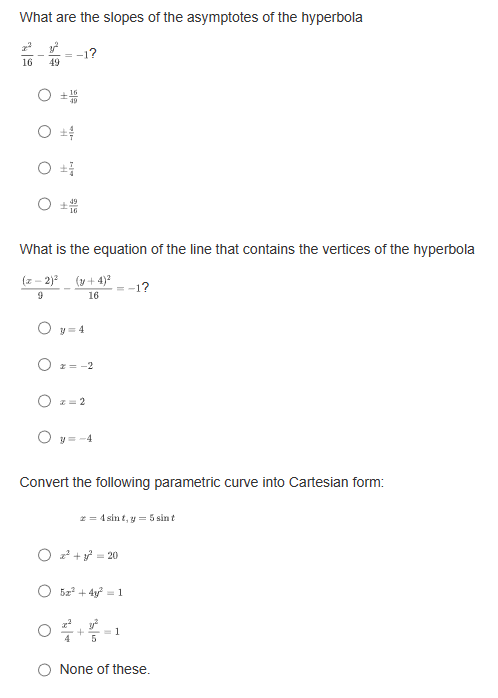

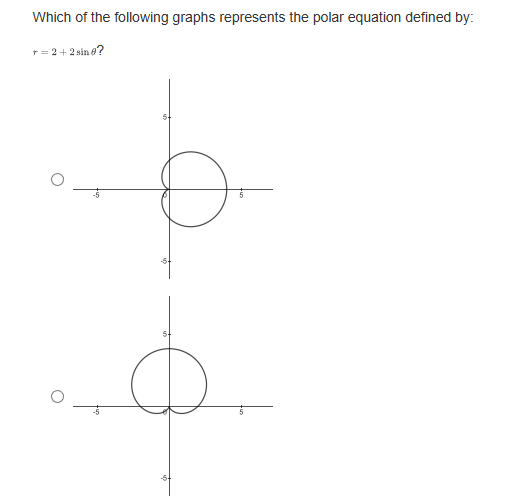
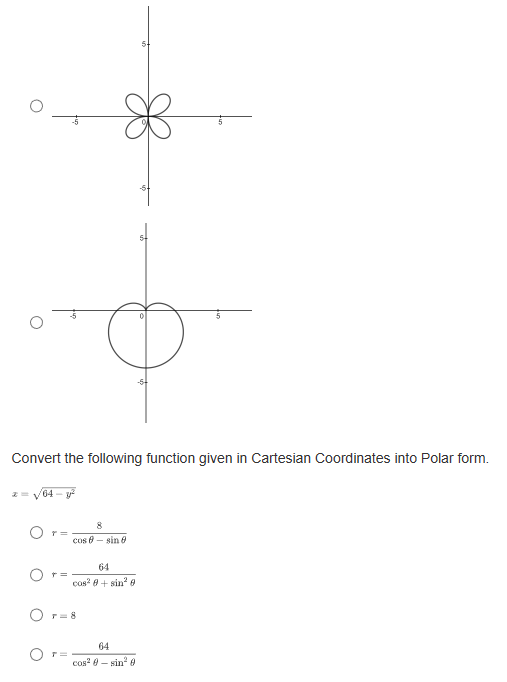
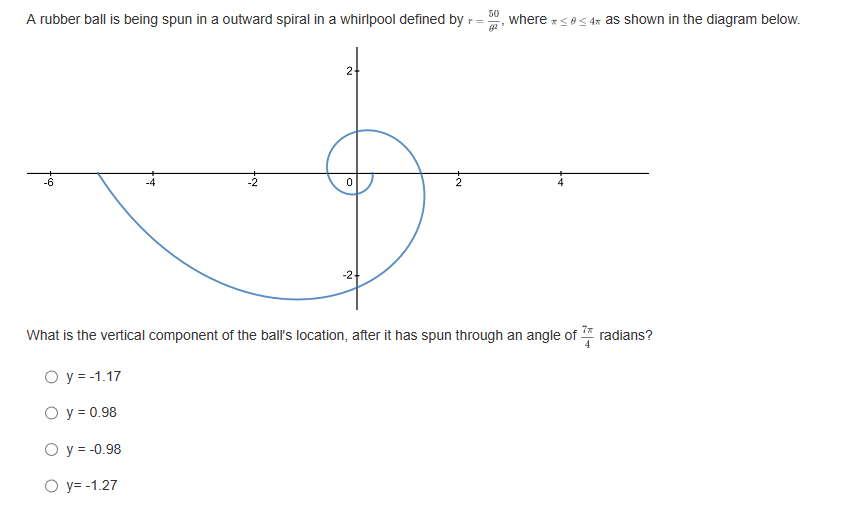
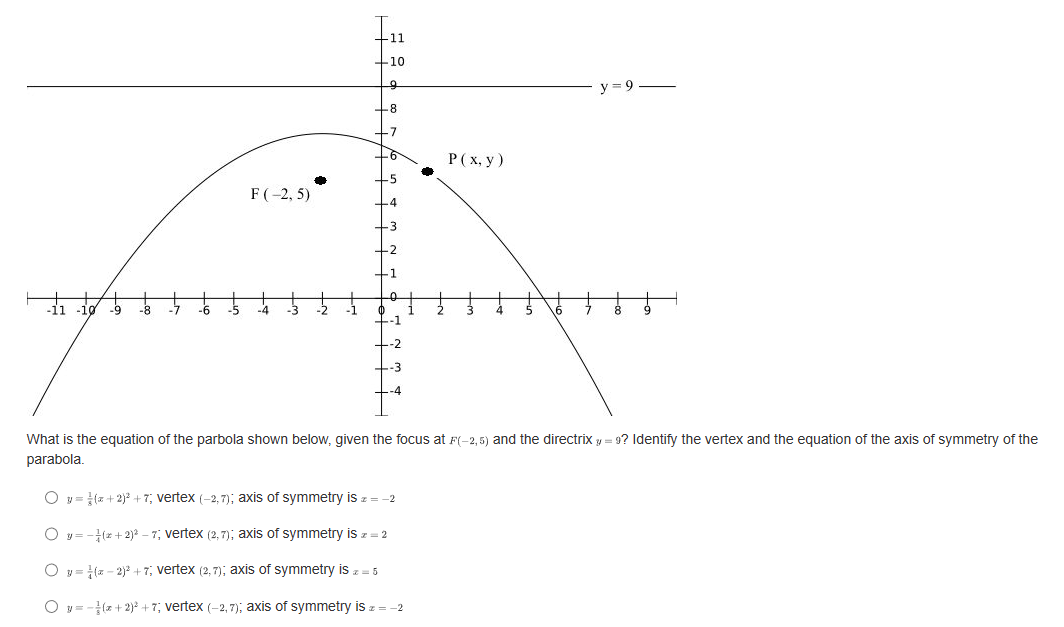
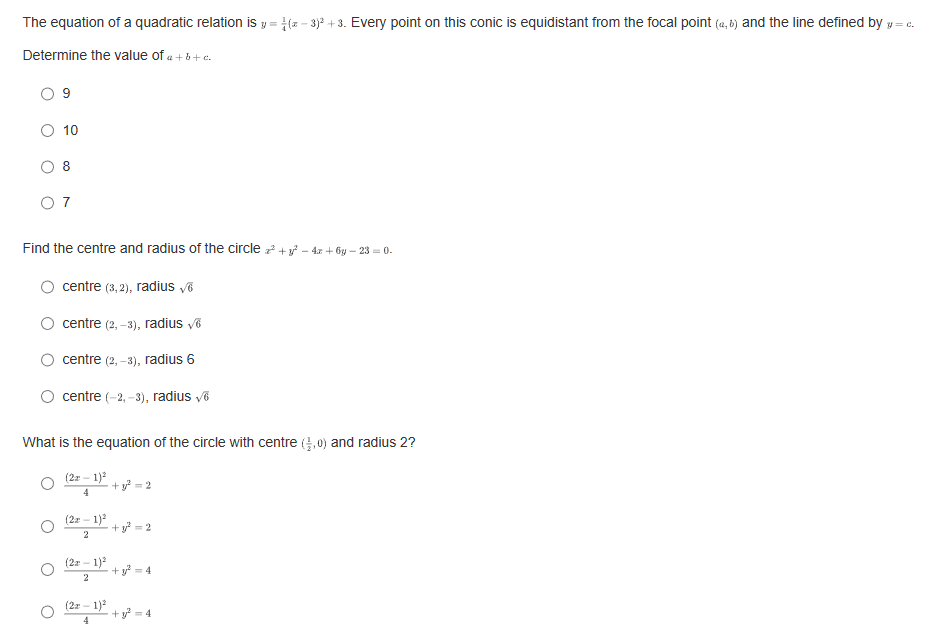
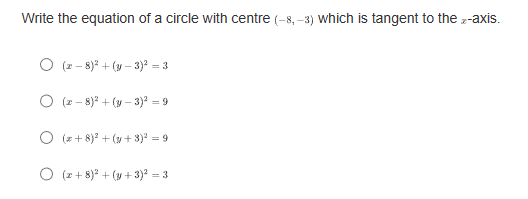
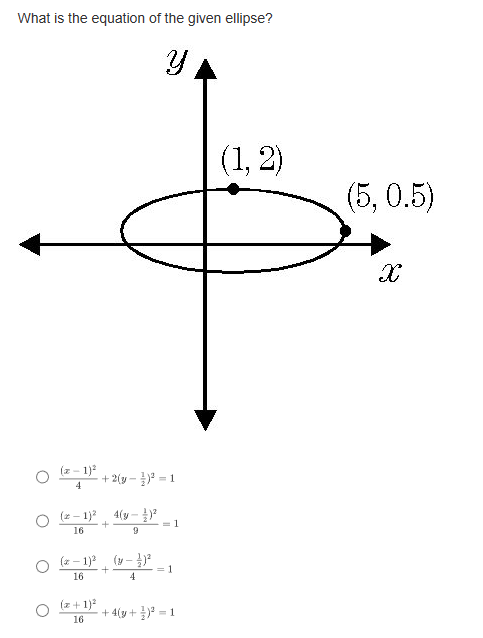


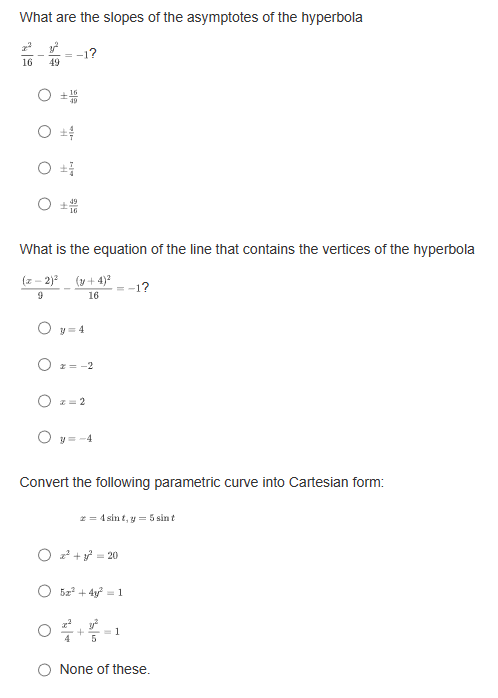

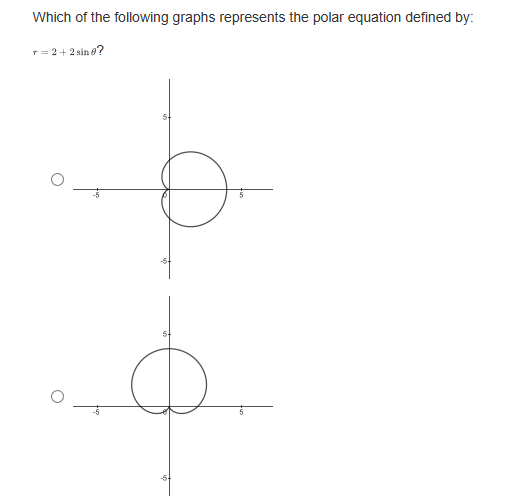
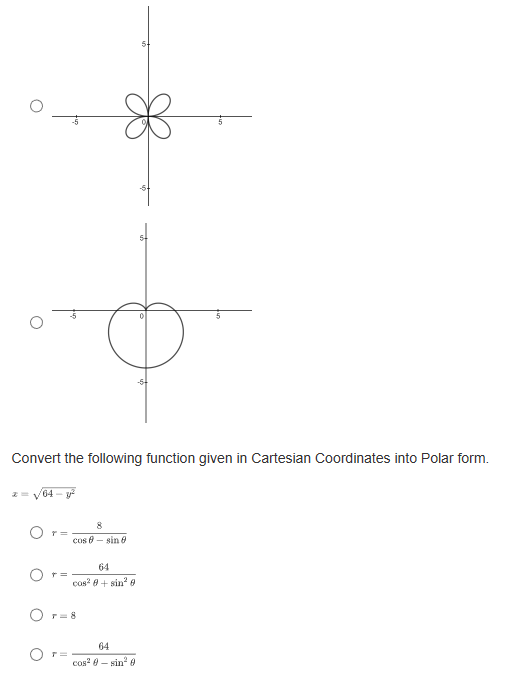
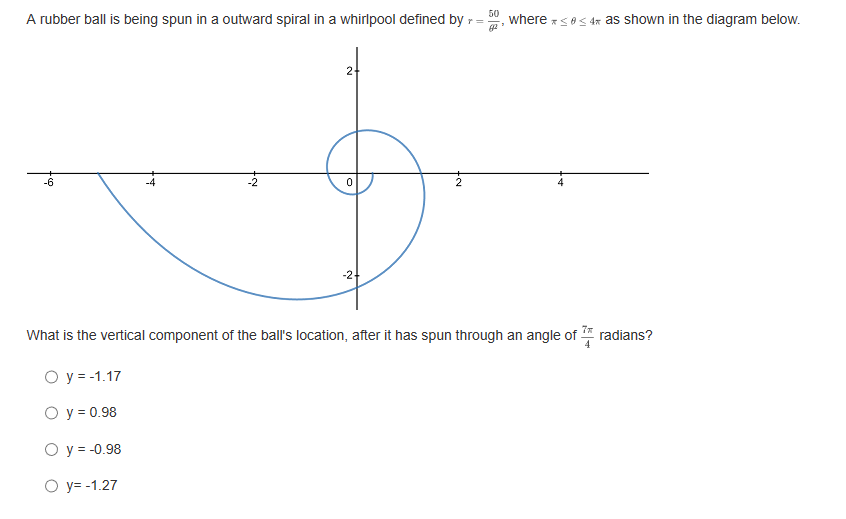
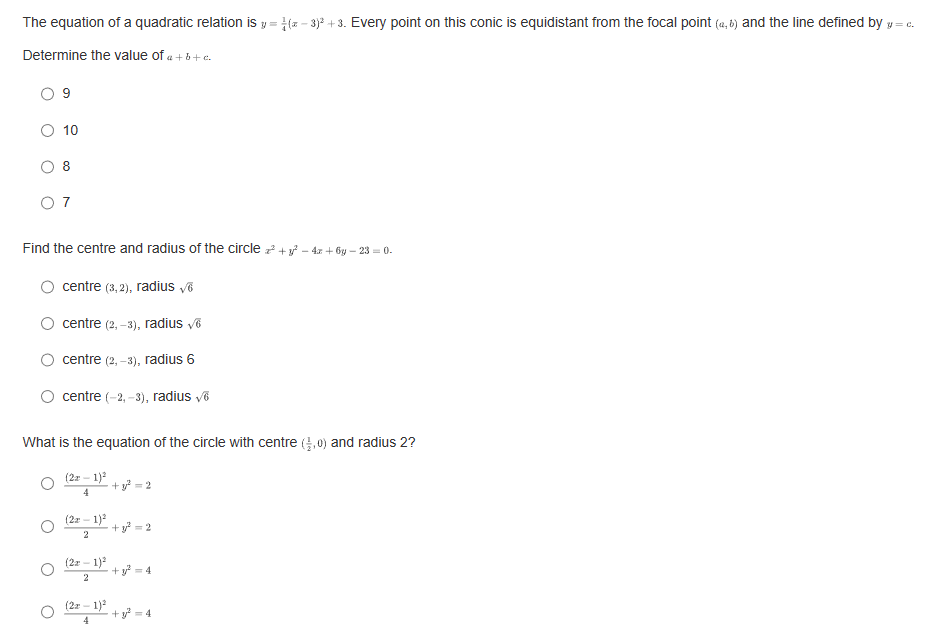
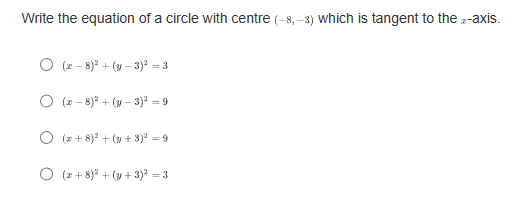
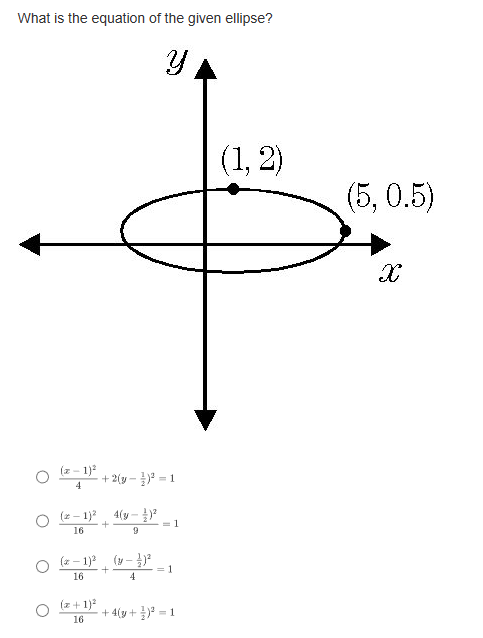

If a parabola's focus is at (3,8) and directrix is at y = 2, what is the vertex form of the equation representing this parabola? O y= - L(2+3) -5 O y= Hz -3)+3 O y= 4(2-3)+5 O y= He+3) +8What are the slopes of the asymptotes of the hyperbola 16 -1? 49 O $10 O O O 1 49 What is the equation of the line that contains the vertices of the hyperbola (z - 2)3 (y +4)2 =-1? 16 0 1= 4 0 1= -2 O 1=-4 Convert the following parametric curve into Cartesian form: + = 4sint, y = 5 sint O 2' + = 20 O ba +4y' = 1 O 4 O None of these.Which of the following is a parameterization of the line that passes through the point (1, -3) with a slope of -4? O z = 2t and y = -8t - 7, for any + O z = 3t and y= -4t - 2, for any t O z=1+3 and y= -4 +1, for any t O z = 2tan and y= -stant + 1, for -t
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


