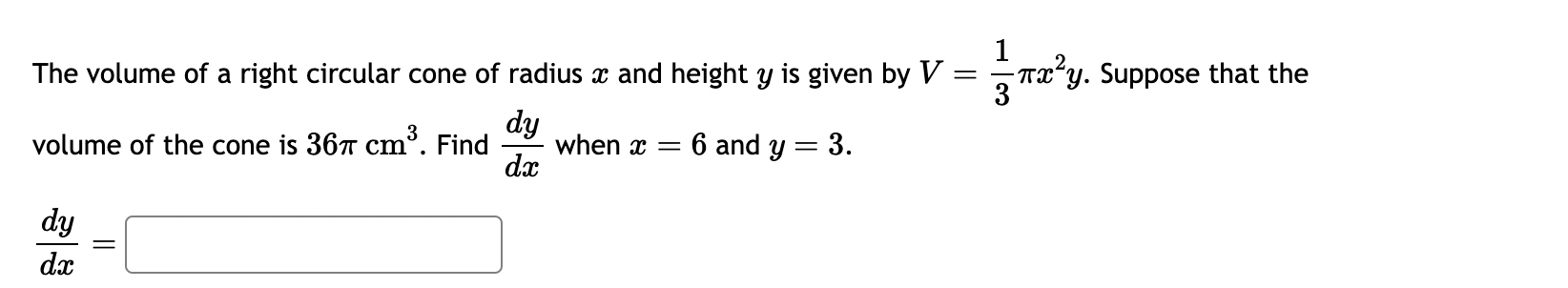
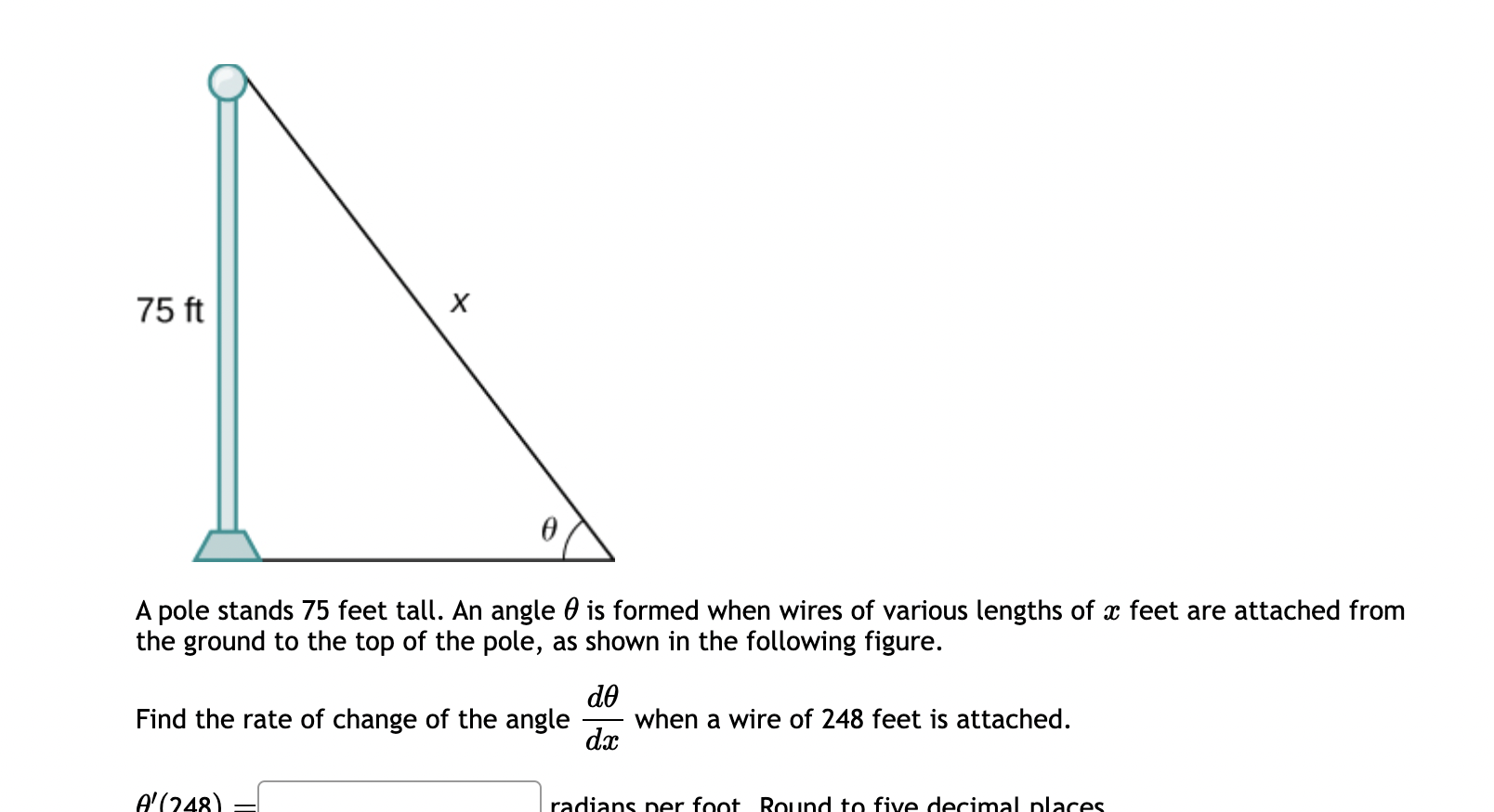
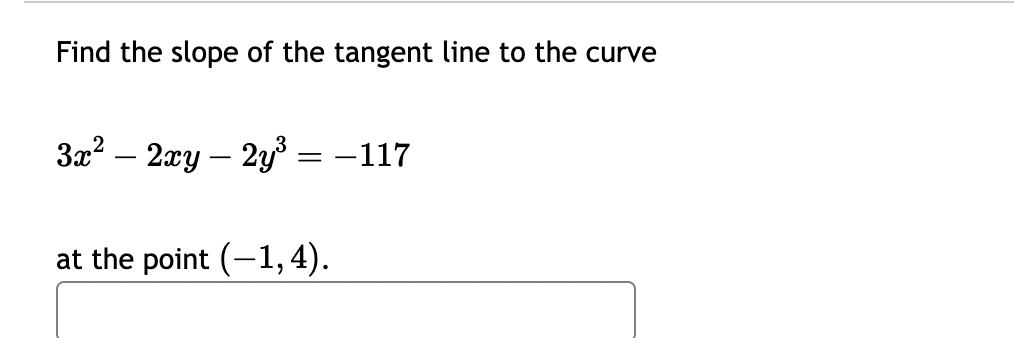
If f(x) = 7 sin(), then f'(x) = Find the slope of the tangent line to the curve 4x + xy 2y = 36 - at the point (-2, 2). The volume of a right circular cone of radius x and height y is given by V dy volume of the cone is 36 cm. Find when x = 6 and y = 3. dx dx 33 dy = 1 -xy. Suppose that the If f(x) = 6e* 2x + 38, find f'(x). - A street light is at the top of a 16 ft tall pole. A woman 6 ft tall walks away from the pole with a speed of 7 ft/sec along a straight path. How fast is the tip of her shadow moving when she is 45 ft from the base of the pole? ft sec A circle is inside a square. The radius of the circle is decreasing at a rate of 5 meters per hour and the sides of the square are decreasing at a rate of 2 meters per hour. When the radius is 4 meters, and the sides are 18 meters, then how fast is the AREA outside the circle but inside the square changing? The rate of change of the area enclosed between the circle and the square is meters per hour. square If f(y) f'(y) = = tan (3y), find f'(y). Use exact values. 75 ft X A pole stands 75 feet tall. An angle 0 is formed when wires of various lengths of x feet are attached from the ground to the top of the pole, as shown in the following figure. de Find the rate of change of the angle when a wire of 248 feet is attached. dx A'(248) radians per foot Round to five decimal places. Find the slope of the tangent line to the curve 3x -2xy - 2y: = -117 at the point (-1,4). Consider a closed rectangular box with a square base with side x and height y. a. Find an equation for the surface area of the rectangular box. S(x, y) = b. If the surface area of the rectangular box is 144 square feet, find dy dx when x = 6 feet and y = 3 feet. dy dx = Find the derivative of f(x) = x6e7x. f'(x) = If f(x)=5xln(x), find f'(x). Find f'(4). If f(y) = tan(3y), find f'(y). Use exact values. f'(y) = Find the slope of the tangent line to the curve 3x - 2xy - 2y -117 == at the point (-1,4).